Интеграл от вектора по вектору (5 видео)

Интегрирование вектор функции

Задачи, возникающие при интегрировании векторных функций, обычно параллельны соответствующим задачам (гл. Радона, которые рассматриваются как непрерывные линейные отображения пространства непрерывных функций в отделимое локально выпуклое пространство.

При доказательстве этого утверждения используются некоторые факты из теории интегрирования векторных функций, выходящие за рамки данной книги [3].

Известны и весьма подробно изучены также многие другие подходы к интегрированию векторных функций; некоторые из них основаны на более прямом определении интеграла как предела сумм.

Случай векторных функций и скалярных мер представляет собой не столь уж коренное обобщение в отличие от случая векторных мер и скалярных функций. Около 30 лет тому назад задача интегрирования векторных функций по скалярной мере была очень популярна.

Если q — скалярная функция, то метод отыскания ее среднего значения хорошо известен. Если же это векторная функция, то нам следует отыскивать ее среднее значение, руководствуясь правилами интегрирования векторных функций.

Теперь мы покажем, что некоторые хорошо известные замкнутые подпространства некоторых других банаховых пространств не дополняемы. Не дополняемость будет установлена с помощью одной довольно общей теоремы о компактных группах операторов, имеющих общее инвариантное подпространство; доказательство этой теоремы использует интегрирование векторных функций по мере Хаара.

Понятие производной вектор функции позволяет дать определение неопределенного интеграла.

Пусть даны две вектор-функции A (t) и B (t). Тогда B (t) называется неопределенным интегралом (первообразной) A (t), если = A(t) и обозначается как:

(2.1)

В, С — постоянный вектор (векторная константа) и это выражение следует понимать как три независимых интеграла от функций в какой-либо системе координат, в частности, в декартовой.

Градиент скалярной функции (декартова система координат):

(2.2)

Градиент скалярной функции имеет геометрическую интерпретацию, вытекающую из следующих рассуждений. Приращение при изменении r на d r = i dx+ j dy + k dz равно с учетом:

(2.3)

Рассмотрим далее две точки, лежащие на поверхности на расстоянии dr друг от друга. При перемещении из одной точки в другую dφ = 0 следовательно, на основании (2.3) gradϕ*dr = 0.

Отсюда gradϕ перпендикулярен поверхности ϕ = const в любой точке. Если рассмотреть случай, когда dr направлен от одной поверхности ϕ = c1 к соседней ϕ = c2, то dϕ = 4c = gradϕ*dr. Для данного dϕ, |dr| — минимален, если dr параллелен gradϕ. Следовательно, градиент скалярной функции есть вектор, указывающий направление максимальной скорости изменения функции ϕ.

Дивергенция вектора (декартова система координат):

(2.4)

Ротор вектора (декартова система координат):

(2.5)

Среди интегральных соотношений важнейшее значение для векторного анализа имеют две теоремы. Теорема Остроградского — Гаусса:

(2.6)

Здесь S -поверхность, ограничивающая объем V , n — нормаль к поверхности. Интеграл по поверхности (в общем случае не замкнутой) вида ʃ b*ds называется потоком вектора b через поверхность.

Вторая теорема — теорема Стокса:

ʃv (2.7)

где S — поверхность, опирающаяся на контур L.

СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ

1. А. К. Боярчук, Г. П. Головач, «Дифференциальные уравнения в примерах и задачах»; Эдиториал УРСС, 2001.

2. А. Н. Тихонов, В. А. Ильин, А. Г. Свешников, «Дифференциальные уравнения», выпуск 7; «Наука», 1980.

3. А. Б. Васильева, Г. Н. Медведев, Н. А. Тихонов, Т. А. Уразгильдина, «Дифференциальное и интегральное исчисление в примерах и задачах»; ФИЗМАТЛИТ, 2003.

4. Бурбаки Н. Интегрирование. Векторное интегрирование. Мера Хаара. Свертка и представления. М.: Наука, 1970. -320 с.

5. В. В. Степанов, «Курс дифференциальных уравнений».

6. Кириченко Б.И., Суетина Н.Л. Дифференцирование и интегрирование .Ульяновск: УлГТУ, 2002, — 32 с.

7. М.Л. Краснов. Вся высшая математика, 2012.

8. Справочное пособие по высшей математике (Антидемидович ). ( В 5-ти томах) Боярчук А.К. и др. Том 2. Математический анализ: ряды, функции векторного аргумента.-2003, 224 с.

9. Справочное пособие по высшей математике (Антидемидович ). ( В 5-ти томах) Боярчук А.К. и др. Том 5. Дифференциальные уравнения в примерах и задачах.-2001, 384 с.

Видео:АО МФТИ 2021-2022 | Производная, интеграл, вектор-функцияСкачать

Интегралы от вектор-функций

Интегралы от вектор-функций. Кроме того, как определяется Интеграл числовой функции, его значение может также определять Интеграл векторной функции, принадлежащей «размерному векторному пространству Пη» (см.§ 18.4). * ’О. Бонне (1819-1892) французский математик. 16 Кудрявцев Ю. Д. Вып. Один 482§ 30.An выражение для замены переменной интегрирования на часть α^^ ^ 6 как векторная функция, m = <^ = oИнтервал[a, b], EE [A_b 4], A11 = 7,—/ r_b r = 1, 2,…разделы R0, BM-это малость раздела M. * » Пт]] р(б) м <、 Интеграл функции r (I) на интервале[a, b]называется независимо от выбора последовательности разбиения、 б $ г(1) И.

Для векторных функций справедливы предложения, аналогичные основной теореме вычисления интеграла. Людмила Фирмаль

Но… Для констант A и B-постоянный вектор пусть R (()=(ХХ (/), хп(1))). Координаты Тора складываются, векторы умножаются на число, координаты умножаются на то же число, а пределы векторной функции равны векторам с координатами, которые являются пределами соответствующих координат.、 Это уравнение переносит многие характеристики Интеграла числовой функции на Интеграл вектора function. In в частности, векторная функция P ( <), определенная в конечных или бесконечных интервалах e числовой линии, является равенством P ( / ) = r ((), во всех внутренних точках I данной функции r (C e En), и на обоих концах интервала E, который переходит в E, функция P непрерывна.

Если векторная функция r (() = rHn интегрируема с сегментами [o, b] и смежна с их внутренними точками (особенно если они смежны с сегментами [a, k]), то в этом сегменте есть примитив. И любой примитив P <1), Формула Р ’(1) У = Р(В) Р(А） Но… * ’Понятие ограничения в данном случае рассматривается и представляется читателю в§ 27.1, полностью аналогичном случаю скалярных функций, которые определяются с использованием ограничений векторной последовательности или на языке (e-6). 31.1.

Определение мер открытого набора (область) 483. Как и в случае скалярных функций, его называют выражением Ньютона-Лейбница. Справедливость этого утверждения основана на справедливости формулы Ньютона-Лейбница для всех координат функции r (()). Замечание. В разделе 15.2 доказаны следующие теоремы: если векторная функция r (1) непрерывна на интервале[a, 6]и дифференцируема внутри него, то существует точка ee (a, b). | Р(6) р(а)| ^ | р ’(б)(б-а). Доказательство этого утверждения, приведенное в разделе 15.2, было по существу несколько искусственным, и необходимо было вывести использование вспомогательных функций.

Используя понятие интеграла (предполагая непрерывность производных рассматриваемых векторных функций), доказательство может быть выполнено более естественным образом. Людмила Фирмаль

Предположим, что векторная функция r (f) enn имеет непрерывную производную на интервале[a, b].Далее, применяя формулу Ньютона-Лейбница, получаем: r ’(01 и С правой стороны получается Интеграл непрерывной скалярной функции. Согласно теореме об интегральном среднем значении (см. результаты теоремы 28.2 1), такие точки существуют. e e(a, b)и др. 1У $’(0 У = Р’(1)(Б-а） Но… И так оно и есть.、 р(б)-р(а) ^ р ’(1)(Б-а), я =(А, Б). Я не уверен.

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

Видео:Математический анализ, 47 урок, Криволинейные интегралы первого родаСкачать

Векторные интегралы; криволинейный интеграл от V Ψ

В предыдущей главе мы видели, что брать производные от поля можно по-разному. Одни приводят к векторным полям; другие — к скалярным. Хотя формул было выведено довольно много, все их можно подытожить одним правилом: операторы д/дх, д/ду и дlдz суть три компоненты векторного оператора v. Сейчас нам хотелось бы лучше разобраться в значении производных поля. Тогда мы легче почувствуем смысл векторных уравнений поля.

Мы уже говорили о смысле операции градиента (v на скаляр). Обратимся теперь к смыслу oneраций вычисления дивергенции (расходимости) и ротора (вихря). Толкование этих величин лучше всего сделать на языке векторных интегралов и уравнений, связывающих эти интегралы. Но уравнения эти, к несчастью, нельзя вывести из векторной алгебры при помощи каких-либо легких подстановок, так что вам придется учить их как что-то новое. Одна из этих интегральных формул практически тривиальна, а другие две — нет. Мы выведем их и поясним их смысл. Эти формулы фактически являются математическими теоремами. Они полезны не только для толкования смысла и содержания понятий дивергенции и ротора, но и при разработке общих физических теорий. Для теории полей эти математические теоремы — все равно что теорема о сохранении энергии для механики частиц. Подобные теоремы общего характера очень важны для более глубокого понимания физики. Но вы увидите, что, за немногими простыми исключениями, они мало что дают для решения задач. К счастью, как раз в начале нашег курса многие простые задачи будут решаться именно этими тремя интегральными формулами. Позже, однако, когда задачи станут потруднее, этими простыми методами мы больше обойтись не сможем.

Мы начнем с той интегральной формулы, куда входит градиент. Мысль, которая содержится в ней, очень проста: раз градиент есть быстрота изменения величины поля, то интеграл от этой быстроты даст нам общее изменение поля. Пусть у нас есть скалярное поле ψ(x, у, z). В двух произвольных точках (1) и (2) функция ψ имеет соответственно значения ψ(1) и ψ(2). (Используется такое удобное обозначение: (2) означает точку (х₂, у₂, z₂), а ψ(2) это то же самое, что ψ(x₂, y₂, z₂).] Если Г (гамма) — произвольная кривая, соединяющая (1) и (2) (фиг. 3.1), то справедлива

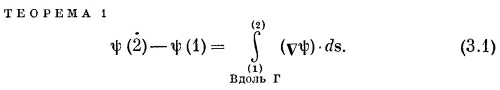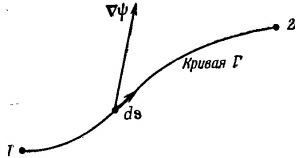
Интеграл, стоящий здесь, это криволинейный интеграл от (1) до (2) вдоль кривой Г от скалярного произведения вектора vψ на другой вектор, ds, являющийся бесконечно малым элементом дуги кривой Г [направленной от (1) к (2)].

Напомним, что мы понимаем под криволинейным интегралом. Рассмотрим скалярную функцию f (х, у, z) и кривую Г, соединяющую две точки (1) и (2). Отметим на кривой множество точек и соединим их хордами, как на фиг. 3.2. Длина ¡-й хорды равна Δs_¡, где ¡ пробегает значения 1, 2, 3. . Под криволинейным интегралом

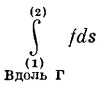подразумевается предел суммы

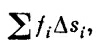где f_¡ — значение функции где-то на ¡-й хорде. Предел — это то, к чему стремится сумма, когда растет число хорд (разумным образом, чтобы даже наибольшее Δs_¡ →0).

В нашей теореме (3.1) интеграл означает то же самое, хоть и выглядит чуть по-иному. Вместо f стоит другой скаляр — составляющая vψ в направлении Δs. Если обозначить эту составляющую через (vψ)_t то ясно, что

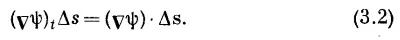Интеграл в (3.1) и подразумевает сумму таких членов.

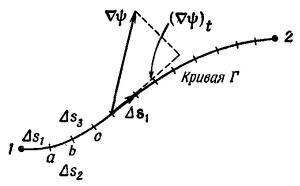
А теперь посмотрим, почему уравнение (3.1) правильно. В гл. 1 мы показали, что составляющая vψ вдоль малого смещения ΔR равна быстроте изменения ψ направлении ΔR. Рассмотрим хорду кривой Δs от точки (1) до точки а на фиг. 3.2. По нашему определению

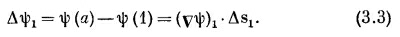Точно так же мы имеем

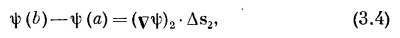где, конечно, (vψ)₁ означает градиент, вычисленный на хорде Δs₁, а (vψ)₂ — градиент, вычисленный на Δs₂. Сложив (3.3) и (3.4), получим

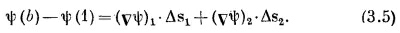Вы видите, что, продолжая прибавлять такие члены, мы получаем в итоге

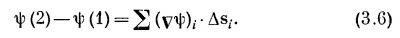Левая часть не зависит от того, как выбирать интервалы — лишь бы точки (1) и (2) были теми же самыми, так что справа можно перейти к пределу. Так доказывается уравнение (3.1). Из нашего доказательства видно, что, подобно тому как равенство не зависит и от выбора точек а,b, с. точно так же оно не зависит от выбора самой кривой Г. Теорема верна для любой кривой, соединяющей точки (1) и (2).

Два слова об обозначениях. Не будет путаницы, если писать для удобства