Содержание

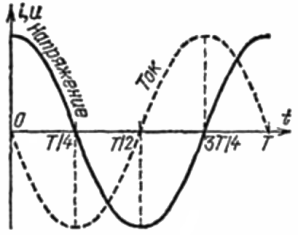
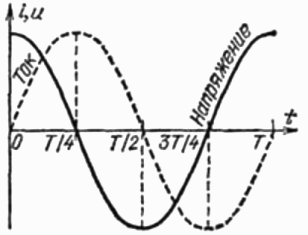
Что такое индуктивная и емкостная нагрузка
Термины «емкостная нагрузка» и «индуктивная нагрузка», применительно к цепям переменного тока, подразумевают определенный характер взаимодействия потребителя с источником переменного напряжения. Грубо это можно проиллюстрировать следующим примером: подключив к розетке полностью разряженный конденсатор, в первый момент времени мы будем наблюдать практически короткое замыкание, тогда как подключив к той же самой розетке катушку индуктивности, в первый момент времени ток через такую нагрузку окажется почти нулевым. Так происходит потому, что катушка и конденсатор взаимодействуют с переменным током принципиально по разному, в чем и заключается ключевое различие между индуктивной и емкостной нагрузками. Емкостная нагрузка Говоря о емкостной нагрузке, имеют ввиду, что она ведет себя в цепи переменного тока подобно конденсатору. Это значит, что синусоидальный переменный ток будет периодически (с удвоенной частотой источника) перезаряжать емкость нагрузки, при этом в первую четверть периода энергия источника будет расходоваться на создание электрического поля между пластинами конденсатора. Во вторую четверть периода энергия электрического поля между пластинами конденсатора будет возвращаться к источнику. В третью четверть периода емкость будет заряжаться от источника противоположной полярностью (по сравнению с тем что было в первую четверть периода). В четвертую четверть периода емкость снова вернет энергию электрического поля обратно в сеть. В течение следующего периода данный цикл повторится. Так ведет себя чисто емкостная нагрузка в цепи синусоидального переменного тока. Практически получается, что при емкостной нагрузке ток опережает по фазе на четверть периода переменное напряжение, приложенное к данной нагрузке, потому что когда емкость заряжается, ток оказывается максимальным уже в первый момент, когда приложенное напряжение источника только начинает нарастать, энергия тока преобразуется в энергию увеличивающегося электрического поля накапливаемого в нагрузке заряда, как в конденсаторе. Но с ростом приложенного напряжения, емкость уже имеет достаточно много накопленного заряда, поэтому с приближением напряжения источника к своему максимуму, скорость накопления заряда в емкостной нагрузке становится меньше, и потребляемый ток при этом уменьшается вплоть до нуля. Примеры емкостных нагрузок: конденсаторные батареи, корректоры коэффициента мощности, синхронные двигатели, ЛЭП сверхвысокого напряжения. Индуктивная нагрузка Если теперь обратить внимание на индуктивную нагрузку, то она ведет себя в цепи переменного тока подобно катушке индуктивности. Это значит, что синусоидальное переменное напряжение будет периодически (с удвоенной частотой источника) порождать ток через индуктивность нагрузки, при этом в первую четверть периода энергия источника будет расходоваться на создание магнитного поля тока через катушку. Во вторую четверть периода энергия магнитного поля катушки будет возвращаться к источнику. В третью четверть периода катушка будет намагничиваться противоположной полярностью (по сравнению с тем что было в первую четверть периода), и в четвертую четверть периода индуктивность снова вернет энергию магнитного поля обратно в сеть. В течение следующего периода данный цикл повторится. Так ведет себя чисто индуктивная нагрузка в цепи синусоидального переменного тока. На деле получается, что при индуктивной нагрузке ток отстает по фазе на четверть периода от переменного напряжения, приложенного к данной нагрузке, потому что когда индуктивность начинает намагничивается, в первый момент времени ток через нее оказывается минимальным, хотя приложенное напряжение источника и находится уже в максимальной точке. Энергия источника преобразуется здесь в энергию увеличивающегося магнитного поля тока, протекающего через индуктивность нагрузки. При уменьшении напряжения, ток через индуктивность уже имеет достаточно большую величину, поэтому с приближением напряжения источника к своему минимуму, скорость роста тока в индуктивной нагрузке замедляется, но сам ток в индуктивности при этом максимален. Примеры индуктивных нагрузок: асинхронные двигатели, электромагниты, дроссели, реакторы, трансформаторы, выпрямители, тиристорные преобразователи. Работа трансформатора под нагрузкой и векторные диаграммы Работа трансформатора зависит от типа нагрузки на вторичной обмотке трансформатора. Нагрузка может быть двух видов: активно-индуктивная и активно-емкостная. Теоретически может быть чисто активная. В зависимости от нагрузки вектор тока I2’ может отставать от ЭДС E2’ на угол ф2, который называется вторичным углом нагрузки. Если нагрузка активно-емкостная, то I2’ опережает ЭДС E2’ на угол нагрузки ф2. Для того чтобы определить ток, проводим вектор, параллельный вектору I2’ и равный ему по величине. Соединяем конец вектора I2’ с началом координат. Так как в режиме нагрузки ток протекает по первичным и вторичным обмоткам трансформатора, напряжение будет отличаться от ЭДС. Строим векторы напряжения. Сначала U1. Для этого из конца вектора E1проводим вектор, параллельный вектору тока I1 и равный r1I1. Из конца этого вектора r1I1 перпендикулярно проводим jx1I1. Векторная диаграмма трансформатора при смешанной активно-индуктивной нагрузке. Векторная диаграмма трансформатора при смешанной активно-ёмкостной нагрузке. Из векторной диаграммы видно, что напряжение U1 не зависит от типа нагрузки и всегда опережает ЭДС E1. Напряжение U2 всегда отстает от ЭДС E2’ и не зависит от типа нагрузки, зато от типа нагрузки зависят угол опережения напряжения U1 и угол отставания напряжения U2. Угол между током I1 и ЭДС E1 обозначается ф1 и называется первичным углом нагрузки. Ток I2’ – ток нагрузки – зависит от величины активной и реактивной составляющих. Если изменить активную составляющую тока нагрузки I2’, изменяется и по длине и по амплитуде ф1. При изменении реактивной составляющей тока I2’ изменяется угол ф2, а длина вектора остается прежней. Упрощенная векторная диаграмма трансформатора при смешанной активно-индуктивной нагрузке. Конденсатор в цепи синусоидального тока Включение в цепи синусоидальной ЭДС Виды включений Конденсатор в цепи постоянного тока (без переменной составляющей) работать, как известно, не может. Обратите внимание! Это утверждение не касается сглаживающих фильтров, где протекает пульсирующий ток, а также специальных блокирующих схем. Совершенно иная картина наблюдается, если рассматривать включение этого элемента в цепи переменного тока, в которой он начинает вести себя более активно и может выполнять сразу несколько функций. В этом случае конденсатор может использоваться в следующих целях: Для блокировки постоянной составляющей, всегда присутствующей в любой электронной схеме; С целью создания сопротивления на пути распространения высокочастотных (ВЧ) компонентов обрабатываемого сигнала; Как ёмкостной нагрузочный элемент, задающий частотные характеристики схемы; В качестве элемента колебательных контуров и специальных фильтров (НЧ и ВЧ). Из всего перечисленного сразу видно, что в подавляющем большинстве случаев конденсатор в цепи переменного тока используется как частотно-зависимый элемент, способный оказывать определённое влияние на протекающие по ней сигналы. Простейший тип включения Происходящие при таком включении процессы приведены на размещённом ниже рисунке. Эпюры переменных процессов Они могут быть описаны путём введения понятия гармонической (синусоидальной) ЭДС, выражаемой как U = Uo cos ω t, и выглядят следующим образом: При нарастании переменной ЭДС конденсатор заряжается протекающим по нему электрическим током I, максимальным в начальный момент времени. По мере заряда ёмкости величина зарядного тока постепенно уменьшается и полностью обнуляется в тот момент, когда ЭДС достигает своего максимума; Важно! Такое разнонаправленное изменение тока и напряжения приводит к образованию между ними характерного для этого элемента сдвига фаз на 90 градусов. На этом первая четверть периодического колебания заканчивается; Далее синусоидальная ЭДС постепенно убывает, вследствие чего конденсатор начинает разряжаться, и в это время в цепи протекает нарастающий по амплитуде ток. При этом наблюдается то же отставание его по фазе, что было в первой четверти периода; По завершении этой стадии конденсатор полностью разряжается (при этом ЭДС равна нулю), а ток в цепи достигает максимума; По мере нарастания обратного (разрядного) тока ёмкость перезаряжается, вследствие чего ток постепенно снижается до нуля, а ЭДС достигает своего пикового значения (то есть весь процесс возвращается в исходную точку). Далее все описанные процессы повторяются с периодичностью, задаваемой частотой внешней ЭДС. Сдвиг по фазе между током и ЭДС может рассматриваться как некое сопротивление изменению напряжения на конденсаторе (отставание его от токовых колебаний).
Емкостное сопротивление Понятие ёмкости Закон Ома для переменного тока При исследовании процессов, протекающих в цепях с подключённым в них конденсатором, обнаружено, что время заряда и разряда для различных образцов этого элемента существенно отличается одно от другого. На основании данного факта было введено понятие ёмкости, определяемое как способность конденсатора накапливать заряд под воздействием заданного напряжения: После этого изменение заряда на его обкладках со временем можно представить как: Но поскольку Q=CU, то путём несложных вычислений получаем: I = CxdU/dt = ω C Uo cos ω t = Io sin(ω t+90), то есть ток течёт через конденсатор таким образом, что он начинает опережать по фазе напряжение на 90 градусов. Такой же результат получается при использовании других математических подходов к этому электрическому процессу. Векторное представление Для большей наглядности в электротехнике используется векторное представление рассмотренных процессов, а для количественной оценки замедления реакции вводится понятие ёмкостного сопротивления (смотрите фото ниже). Векторное представление тока Из векторной диаграммы также видно, что ток в цепи конденсатора опережает по фазе напряжение на 90 градусов. Дополнительная информация. При изучении «поведения» катушки в цепи синусоидального тока было обнаружено, что он в ней, напротив, отстаёт по фазе от напряжения. И в том, и в другом случае наблюдается различие в фазных характеристиках процессов, свидетельствующих о реактивном характере нагрузки в цепи переменной ЭДС. Упуская из внимания сложные для описания дифференциальные вычисления, для представления сопротивления ёмкостной нагрузки получим: Из неё следует, что создаваемое конденсатором сопротивление обратно пропорционально частоте переменного сигнала и ёмкости установленного в цепь элемента. Указанная зависимость позволяет строить на основе конденсатора такие частотно-зависимые схемы, как: Интегрирующие и дифференцирующие цепочки (совместно с пассивным резистором); НЧ и ВЧ фильтрующие элементы; Реактивные цепи, используемые для улучшения нагрузочных характеристик силового оборудования; Резонансные контуры последовательного и параллельного типа. В первом случае посредством ёмкости удаётся произвольно изменять форму прямоугольных импульсов, увеличивая их длительность (интегрирование) или сокращая её (дифференцирование). Фильтрующие цепочки и резонансные контура широко используются в линейных схемах самого различного класса (усилители, преобразователи, генераторы и подобные им устройства). График ёмкостного сопротивления Доказано, что ток через конденсатор протекает только под воздействием гармонически изменяющегося напряжения. При этом сила тока в цепочке определяется ёмкостью данного элемента, так что чем больше ёмкость конденсатора, тем он значительнее по величине. Но можно проследить и обратную зависимость, в соответствие с которой сопротивление конденсатора возрастает с понижением частотного параметра. В качестве примера рассмотрим график, приведённый на рисунке ниже. График зависимости сопротивления ёмкости от частоты Из приведённой выше зависимости можно сделать следующие важные выводы: Для тока постоянной величины (частота = 0) Хс равно бесконечности, что означает невозможность его протекания в ней; При очень высоких частотах сопротивление этого элемента стремится к нулю; При прочих равных условиях оно определяется ёмкостью установленного в цепи конденсатора. Определённый интерес представляют вопросы распределения электрической энергии в цепях переменного тока с включённым в них конденсатором. Работа (мощность) в ёмкостной нагрузке Подобно случаю с индуктивностью, при исследовании «поведения» конденсатора в цепях переменной ЭДС обнаружено, что расхода мощности в них из-за сдвига фаз U и I не наблюдается. Последнее объясняется тем, что электрическая энергия на начальном этапе процесса (при заряде) запасается между обкладками конденсатора, а на второй его стадии – отдается назад в источник (смотрите рисунок ниже). Работа в цепи с ёмкостью Вследствие этого емкостное сопротивление относится к категории реактивных, или безваттных, нагрузок. Однако такой вывод можно считать чисто теоретическим, поскольку в реальных цепях всегда присутствуют обычные пассивные элементы, обладающие не реактивным, а активным или ваттным сопротивлением. К ним относятся: Сопротивления подводящих проводов; Проводимости диэлектрических зон в конденсаторе; Рассеяние на контактах; Активные сопротивления витков катушек и тому подобное. В связи с этим в любой реальной электрической цепочке всегда имеются потери активной мощности (её рассеяние), определяемые в каждом случае индивидуально. Особое внимание следует обратить на внутренние потери, связанные с утечками через диэлектрик и плохим состоянием изоляции между пластинами (обкладками). Обратимся к следующим определениям, учитывающим реальное положение дел. Так, потери, связанные с качественными характеристиками диэлектрика, называются диэлектрическими. Энергетические затраты, относимые на несовершенство находящейся между пластинами изоляции, принято классифицировать как потери из-за утечек в конденсаторном элементе. В завершении этого обзора интересно проследить за одной аналогией, представляющей процессы, происходящие в конденсаторной цепи с упругой механической пружиной. И, действительно, пружина, подобно этому элементу, в течение одной части периодического колебания накапливает в себе потенциальную энергию, а во второй фазе – отдает её обратно в кинетической форме. На основании такой аналогии может быть представлена вся картина поведения конденсатора в цепях с переменной ЭДС.
Конденсатор – элемент электрической цепи, предназначенный для использования его ёмкости. В конденсаторе накапливается энергия электрического поля. Свойство элемента запасать электрический заряд характеризует ёмкость. Этот параметр является коэффициентом пропорциональности между зарядом q и прикладываемым напряжением u q = C·u, где q – выражается в кулонах [Кл], С – в фарадах [Ф], u – в вольтах [B]. При изменении напряжения на конденсаторе изменяется заряд и возникает электрический ток Идеализированный конденсатор обладает только параметром С. Рассмотрим электрические процессы в цепи с идеальным ёмкостным элементом, рис. 3.6, а. Пусть напряжение источника изменяется по закону u = Um·sinω·t, (ψu = 0). В цепи возникает ток Из полученного выражения видно, что начальная фаза тока ψi = π/2. Угол сдвига фаз между напряжением и током составляет φ = ψu – ψi = 0 – π/2 = — π/2. Рис 3.6 – Схема замещения цепи с емкостным элементом (а), временная (б) и векторная (в) диаграммы Следовательно, синусоида напряжения на емкости отстаёт от синусоиды тока на угол π/2, рис. 3.6, б, в. На практике, если в электрической цепи напряжение отстаёт по фазе от тока, говорят об ёмкостном характере нагрузки. Im = ω·C·Um, Это выражение представляет закон Ома. Величину 1/ω·C называют ёмкостным сопротивлением конденсатора и измеряют в [Ом] Ёмкостное сопротивление имеет место только в том случае, когда происходит изменение напряжения на обкладках конденсатора. При постоянном напряжении (f = 0) ёмкостное сопротивление равно бесконечности (т. е. В цепи будет разрыв). Мгновенная мощность ёмкостного элемента Амплитуда мгновенной мощности равна реактивной мощности QC = U·I = XC·I2. Активная мощность (средняя за период) равна нулю, рис. 3.6, б. С энергетической точки зрения график мгновенной мощности отражает накопление энергии в электрическом поле конденсатора (когда мощность положительная) и возврат её источнику питания (когда мощность отрицательная). Следовательно, ёмкостной элемент является реактивной нагрузкой. Выразим электрические величины в комплексной форме. Напряжение и ток (действующие значения) в цепи имеют вид U = U·ej·ψu, I = I·ej·ψi , ψu = 0, ψi = π/2, φ = — π/2. Комплексное сопротивление цепи Ёмкостное сопротивление является отрицательным мнимым числом. 13 цепь синусоидального тока с реальной катушкой индуктивности. Последовательно соединенные реальная индуктивная катушка и конденсатор в цепи синусоидального тока Катушка с активным сопротивлением R и индуктивностью L и конденсатор емкостью С включены последовательно(рис.6.8). В схеме протекает синусоидальный ток Определим напряжение на входе схемы. В соответствии со вторым законом Кирхгофа, Подставим эти формулы в уравнение (6.15). Получим: Из выражения (6.16) видно: напряжение в активном сопротивлении совпадает по фазе с током, напряжение на индуктивности опережает по фазе ток на 90o, напряжение по емкости отстает по фазе от тока на 90o. Запишем уравнение (6.16) в комплексной форме: Поделим левую и правую части уравнения (6.17) на √2. Получим уравнение для комплексов действующих значений токов и напряжений где — комплексное сопротивление цепи; — модуль комплексного сопротивления, или полное сопротивление цепи; — начальная фаза комплексного сопротивления. При построении векторных диаграмм цепи рассмотрим три случая. XL > XC, цепь носит индуктивный характер. Векторы напряжений на индуктивности и емкости направлены в противоположные стороны, частично компенсируют друг друга. Вектор напряжения на входе схемы опережает вектор тока(рис.6.9). Индуктивное сопротивление меньше емкостного. Вектор напряжения на входе схемы отстает от вектора тока. Цепь носит емкостный характер (рис.6.10). Индуктивное и емкостное сопротивления одинаковы. Напряжения на индуктивности и емкости полностью компенсируют друг друга. Ток в цепи совпадает по фазе с входным напряжением. В электрической цепи наступает режим резонансного напряжения (рис.6.11). Ток в резонансном режиме достигает максимума, так как полное сопротивление (z) цепи имеет минимальное значение. Условие возникновения резонанса: , отсюда резонансная частота равна Из формулы следует, что режима резонанса можно добиться следующими способами: изменением частоты; изменением индуктивности; изменением емкости. В резонансном режиме входное напряжение равно падению напряжения в активном сопротивлении. На индуктивности и емкости схемы могут возникнуть напряжения, во много раз превышающие напряжение на входе цепи. Это объясняется тем, что каждое напряжение равно произведению тока I0 (а он наибольший), на соответствующее индуктивное или емкостное сопротивление (а они могут быть большими). Рис. 6.9 Рис. 6.10 Рис. 6.11 14 цепь синусоидального тока с последовательным соединением активного и емкостного сопротивлений. 15 цепь переменного однофазного тока с последовательным соединением активного, индуктивного и емкостного сопротивлений.
Работа трансформатора под нагрузкой и векторные диаграммы
Конденсатор в цепи синусоидального тока
Включение в цепи синусоидальной ЭДС
Виды включений
Простейший тип включения
Емкостное сопротивление
Понятие ёмкости
Векторное представление
График ёмкостного сопротивления
Работа (мощность) в ёмкостной нагрузке
🔥 Видео

Что такое индуктивная и емкостная нагрузка

Термины «емкостная нагрузка» и «индуктивная нагрузка», применительно к цепям переменного тока, подразумевают определенный характер взаимодействия потребителя с источником переменного напряжения.

Грубо это можно проиллюстрировать следующим примером: подключив к розетке полностью разряженный конденсатор, в первый момент времени мы будем наблюдать практически короткое замыкание, тогда как подключив к той же самой розетке катушку индуктивности, в первый момент времени ток через такую нагрузку окажется почти нулевым.

Так происходит потому, что катушка и конденсатор взаимодействуют с переменным током принципиально по разному, в чем и заключается ключевое различие между индуктивной и емкостной нагрузками.

Емкостная нагрузка

Говоря о емкостной нагрузке, имеют ввиду, что она ведет себя в цепи переменного тока подобно конденсатору.

Это значит, что синусоидальный переменный ток будет периодически (с удвоенной частотой источника) перезаряжать емкость нагрузки, при этом в первую четверть периода энергия источника будет расходоваться на создание электрического поля между пластинами конденсатора. Во вторую четверть периода энергия электрического поля между пластинами конденсатора будет возвращаться к источнику.

В третью четверть периода емкость будет заряжаться от источника противоположной полярностью (по сравнению с тем что было в первую четверть периода). В четвертую четверть периода емкость снова вернет энергию электрического поля обратно в сеть. В течение следующего периода данный цикл повторится. Так ведет себя чисто емкостная нагрузка в цепи синусоидального переменного тока.

Практически получается, что при емкостной нагрузке ток опережает по фазе на четверть периода переменное напряжение, приложенное к данной нагрузке, потому что когда емкость заряжается, ток оказывается максимальным уже в первый момент, когда приложенное напряжение источника только начинает нарастать, энергия тока преобразуется в энергию увеличивающегося электрического поля накапливаемого в нагрузке заряда, как в конденсаторе.

Но с ростом приложенного напряжения, емкость уже имеет достаточно много накопленного заряда, поэтому с приближением напряжения источника к своему максимуму, скорость накопления заряда в емкостной нагрузке становится меньше, и потребляемый ток при этом уменьшается вплоть до нуля.

Примеры емкостных нагрузок: конденсаторные батареи, корректоры коэффициента мощности, синхронные двигатели, ЛЭП сверхвысокого напряжения.

Индуктивная нагрузка

Если теперь обратить внимание на индуктивную нагрузку, то она ведет себя в цепи переменного тока подобно катушке индуктивности.

Это значит, что синусоидальное переменное напряжение будет периодически (с удвоенной частотой источника) порождать ток через индуктивность нагрузки, при этом в первую четверть периода энергия источника будет расходоваться на создание магнитного поля тока через катушку.

Во вторую четверть периода энергия магнитного поля катушки будет возвращаться к источнику. В третью четверть периода катушка будет намагничиваться противоположной полярностью (по сравнению с тем что было в первую четверть периода), и в четвертую четверть периода индуктивность снова вернет энергию магнитного поля обратно в сеть.

В течение следующего периода данный цикл повторится. Так ведет себя чисто индуктивная нагрузка в цепи синусоидального переменного тока.

На деле получается, что при индуктивной нагрузке ток отстает по фазе на четверть периода от переменного напряжения, приложенного к данной нагрузке, потому что когда индуктивность начинает намагничивается, в первый момент времени ток через нее оказывается минимальным, хотя приложенное напряжение источника и находится уже в максимальной точке.

Энергия источника преобразуется здесь в энергию увеличивающегося магнитного поля тока, протекающего через индуктивность нагрузки. При уменьшении напряжения, ток через индуктивность уже имеет достаточно большую величину, поэтому с приближением напряжения источника к своему минимуму, скорость роста тока в индуктивной нагрузке замедляется, но сам ток в индуктивности при этом максимален.

Примеры индуктивных нагрузок: асинхронные двигатели, электромагниты, дроссели, реакторы, трансформаторы, выпрямители, тиристорные преобразователи.

Видео:Построение векторных диаграмм/Треугольник токов, напряжений и мощностей/Коэффициент мощностиСкачать

Работа трансформатора под нагрузкой и векторные диаграммы

Работа трансформатора зависит от типа нагрузки на вторичной обмотке трансформатора. Нагрузка может быть двух видов: активно-индуктивная и активно-емкостная. Теоретически может быть чисто активная. В зависимости от нагрузки вектор тока I₂’ может отставать от ЭДС E₂’ на угол ф₂, который называется вторичным углом нагрузки.

Если нагрузка активно-емкостная, то I₂’ опережает ЭДС E₂’ на угол нагрузки ф₂.

Для того чтобы определить ток, проводим вектор, параллельный вектору I₂’ и равный ему по величине. Соединяем конец вектора I₂’ с началом координат. Так как в режиме нагрузки ток протекает по первичным и вторичным обмоткам трансформатора, напряжение будет отличаться от ЭДС.

Строим векторы напряжения. Сначала U₁. Для этого из конца вектора E1проводим вектор, параллельный вектору тока I₁ и равный r₁I₁. Из конца этого вектора r₁I₁ перпендикулярно проводим jx₁I₁.

Векторная диаграмма трансформатора при смешанной активно-индуктивной нагрузке.

Векторная диаграмма трансформатора при смешанной активно-ёмкостной нагрузке.

Из векторной диаграммы видно, что напряжение U₁ не зависит от типа нагрузки и всегда опережает ЭДС E₁.

Напряжение U₂ всегда отстает от ЭДС E₂’ и не зависит от типа нагрузки, зато от типа нагрузки зависят угол опережения напряжения U₁ и угол отставания напряжения U₂.

Угол между током I₁ и ЭДС E₁ обозначается ф₁ и называется первичным углом нагрузки.

Ток I₂’ – ток нагрузки – зависит от величины активной и реактивной составляющих.

Если изменить активную составляющую тока нагрузки I₂’, изменяется и по длине и по амплитуде ф₁. При изменении реактивной составляющей тока I₂’ изменяется угол ф₂, а длина вектора остается прежней.

Упрощенная векторная диаграмма трансформатора при смешанной активно-индуктивной нагрузке.

Видео:Векторные диаграммы и коэффициент мощностиСкачать

Конденсатор в цепи синусоидального тока

Видео:Реактивная мощность за 5 минут простыми словами. Четкий #энерголикбезСкачать

Включение в цепи синусоидальной ЭДС

Виды включений

Конденсатор в цепи постоянного тока (без переменной составляющей) работать, как известно, не может.

Обратите внимание! Это утверждение не касается сглаживающих фильтров, где протекает пульсирующий ток, а также специальных блокирующих схем.

Совершенно иная картина наблюдается, если рассматривать включение этого элемента в цепи переменного тока, в которой он начинает вести себя более активно и может выполнять сразу несколько функций. В этом случае конденсатор может использоваться в следующих целях:

Для блокировки постоянной составляющей, всегда присутствующей в любой электронной схеме;
С целью создания сопротивления на пути распространения высокочастотных (ВЧ) компонентов обрабатываемого сигнала;
Как ёмкостной нагрузочный элемент, задающий частотные характеристики схемы;
В качестве элемента колебательных контуров и специальных фильтров (НЧ и ВЧ).

Из всего перечисленного сразу видно, что в подавляющем большинстве случаев конденсатор в цепи переменного тока используется как частотно-зависимый элемент, способный оказывать определённое влияние на протекающие по ней сигналы.

Простейший тип включения

Происходящие при таком включении процессы приведены на размещённом ниже рисунке.

Эпюры переменных процессов

Они могут быть описаны путём введения понятия гармонической (синусоидальной) ЭДС, выражаемой как U = Uo cos ω t, и выглядят следующим образом:

При нарастании переменной ЭДС конденсатор заряжается протекающим по нему электрическим током I, максимальным в начальный момент времени. По мере заряда ёмкости величина зарядного тока постепенно уменьшается и полностью обнуляется в тот момент, когда ЭДС достигает своего максимума;

Важно! Такое разнонаправленное изменение тока и напряжения приводит к образованию между ними характерного для этого элемента сдвига фаз на 90 градусов.

На этом первая четверть периодического колебания заканчивается;
Далее синусоидальная ЭДС постепенно убывает, вследствие чего конденсатор начинает разряжаться, и в это время в цепи протекает нарастающий по амплитуде ток. При этом наблюдается то же отставание его по фазе, что было в первой четверти периода;
По завершении этой стадии конденсатор полностью разряжается (при этом ЭДС равна нулю), а ток в цепи достигает максимума;
По мере нарастания обратного (разрядного) тока ёмкость перезаряжается, вследствие чего ток постепенно снижается до нуля, а ЭДС достигает своего пикового значения (то есть весь процесс возвращается в исходную точку).

Далее все описанные процессы повторяются с периодичностью, задаваемой частотой внешней ЭДС. Сдвиг по фазе между током и ЭДС может рассматриваться как некое сопротивление изменению напряжения на конденсаторе (отставание его от токовых колебаний).

Видео:Коэффициент мощности простыми словамиСкачать

Емкостное сопротивление

Понятие ёмкости

Закон Ома для переменного тока

При исследовании процессов, протекающих в цепях с подключённым в них конденсатором, обнаружено, что время заряда и разряда для различных образцов этого элемента существенно отличается одно от другого. На основании данного факта было введено понятие ёмкости, определяемое как способность конденсатора накапливать заряд под воздействием заданного напряжения:

После этого изменение заряда на его обкладках со временем можно представить как:

Но поскольку Q=CU, то путём несложных вычислений получаем:

I = CxdU/dt = ω C Uo cos ω t = Io sin(ω t+90),

то есть ток течёт через конденсатор таким образом, что он начинает опережать по фазе напряжение на 90 градусов. Такой же результат получается при использовании других математических подходов к этому электрическому процессу.

Векторное представление

Для большей наглядности в электротехнике используется векторное представление рассмотренных процессов, а для количественной оценки замедления реакции вводится понятие ёмкостного сопротивления (смотрите фото ниже).

Векторное представление тока

Из векторной диаграммы также видно, что ток в цепи конденсатора опережает по фазе напряжение на 90 градусов.

Дополнительная информация. При изучении «поведения» катушки в цепи синусоидального тока было обнаружено, что он в ней, напротив, отстаёт по фазе от напряжения.

И в том, и в другом случае наблюдается различие в фазных характеристиках процессов, свидетельствующих о реактивном характере нагрузки в цепи переменной ЭДС.

Упуская из внимания сложные для описания дифференциальные вычисления, для представления сопротивления ёмкостной нагрузки получим:

Из неё следует, что создаваемое конденсатором сопротивление обратно пропорционально частоте переменного сигнала и ёмкости установленного в цепь элемента. Указанная зависимость позволяет строить на основе конденсатора такие частотно-зависимые схемы, как:

Интегрирующие и дифференцирующие цепочки (совместно с пассивным резистором);
НЧ и ВЧ фильтрующие элементы;
Реактивные цепи, используемые для улучшения нагрузочных характеристик силового оборудования;
Резонансные контуры последовательного и параллельного типа.

В первом случае посредством ёмкости удаётся произвольно изменять форму прямоугольных импульсов, увеличивая их длительность (интегрирование) или сокращая её (дифференцирование).

Фильтрующие цепочки и резонансные контура широко используются в линейных схемах самого различного класса (усилители, преобразователи, генераторы и подобные им устройства).

График ёмкостного сопротивления

Доказано, что ток через конденсатор протекает только под воздействием гармонически изменяющегося напряжения. При этом сила тока в цепочке определяется ёмкостью данного элемента, так что чем больше ёмкость конденсатора, тем он значительнее по величине.

Но можно проследить и обратную зависимость, в соответствие с которой сопротивление конденсатора возрастает с понижением частотного параметра. В качестве примера рассмотрим график, приведённый на рисунке ниже.

График зависимости сопротивления ёмкости от частоты

Из приведённой выше зависимости можно сделать следующие важные выводы:

Для тока постоянной величины (частота = 0) Хс равно бесконечности, что означает невозможность его протекания в ней;
При очень высоких частотах сопротивление этого элемента стремится к нулю;
При прочих равных условиях оно определяется ёмкостью установленного в цепи конденсатора.

Определённый интерес представляют вопросы распределения электрической энергии в цепях переменного тока с включённым в них конденсатором.

Работа (мощность) в ёмкостной нагрузке

Подобно случаю с индуктивностью, при исследовании «поведения» конденсатора в цепях переменной ЭДС обнаружено, что расхода мощности в них из-за сдвига фаз U и I не наблюдается. Последнее объясняется тем, что электрическая энергия на начальном этапе процесса (при заряде) запасается между обкладками конденсатора, а на второй его стадии – отдается назад в источник (смотрите рисунок ниже).

Работа в цепи с ёмкостью

Вследствие этого емкостное сопротивление относится к категории реактивных, или безваттных, нагрузок. Однако такой вывод можно считать чисто теоретическим, поскольку в реальных цепях всегда присутствуют обычные пассивные элементы, обладающие не реактивным, а активным или ваттным сопротивлением. К ним относятся:

Сопротивления подводящих проводов;
Проводимости диэлектрических зон в конденсаторе;
Рассеяние на контактах;
Активные сопротивления витков катушек и тому подобное.

В связи с этим в любой реальной электрической цепочке всегда имеются потери активной мощности (её рассеяние), определяемые в каждом случае индивидуально.

Особое внимание следует обратить на внутренние потери, связанные с утечками через диэлектрик и плохим состоянием изоляции между пластинами (обкладками). Обратимся к следующим определениям, учитывающим реальное положение дел. Так, потери, связанные с качественными характеристиками диэлектрика, называются диэлектрическими. Энергетические затраты, относимые на несовершенство находящейся между пластинами изоляции, принято классифицировать как потери из-за утечек в конденсаторном элементе.

В завершении этого обзора интересно проследить за одной аналогией, представляющей процессы, происходящие в конденсаторной цепи с упругой механической пружиной. И, действительно, пружина, подобно этому элементу, в течение одной части периодического колебания накапливает в себе потенциальную энергию, а во второй фазе – отдает её обратно в кинетической форме. На основании такой аналогии может быть представлена вся картина поведения конденсатора в цепях с переменной ЭДС.

Конденсатор – элемент электрической цепи, предназначенный для использования его ёмкости. В конденсаторе накапливается энергия электрического поля. Свойство элемента запасать электрический заряд характеризует ёмкость. Этот параметр является коэффициентом пропорциональности между зарядом q и прикладываемым напряжением u

q = C·u,

где q – выражается в кулонах [Кл], С – в фарадах [Ф], u – в вольтах [B].

При изменении напряжения на конденсаторе изменяется заряд и возникает электрический ток

Идеализированный конденсатор обладает только параметром С.

Рассмотрим электрические процессы в цепи с идеальным ёмкостным элементом, рис. 3.6, а.

Пусть напряжение источника изменяется по закону

u = Um·sinω·t, (ψu = 0).

В цепи возникает ток

Из полученного выражения видно, что начальная фаза тока ψi = π/2. Угол сдвига фаз между напряжением и током составляет

φ = ψu – ψi = 0 – π/2 = — π/2.

Рис 3.6 – Схема замещения цепи с емкостным элементом (а), временная (б) и векторная (в) диаграммы

Следовательно, синусоида напряжения на емкости отстаёт от синусоиды тока на угол π/2, рис. 3.6, б, в. На практике, если в электрической цепи напряжение отстаёт по фазе от тока, говорят об ёмкостном характере нагрузки.

Im = ω·C·Um,

Это выражение представляет закон Ома. Величину 1/ω·C называют ёмкостным сопротивлением конденсатора и измеряют в [Ом]

Ёмкостное сопротивление имеет место только в том случае, когда происходит изменение напряжения на обкладках конденсатора. При постоянном напряжении (f = 0) ёмкостное сопротивление равно бесконечности (т. е. В цепи будет разрыв).

Мгновенная мощность ёмкостного элемента

Амплитуда мгновенной мощности равна реактивной мощности

QC = U·I = XC·I2.

Активная мощность (средняя за период) равна нулю, рис. 3.6, б.

С энергетической точки зрения график мгновенной мощности отражает накопление энергии в электрическом поле конденсатора (когда мощность положительная) и возврат её источнику питания (когда мощность отрицательная). Следовательно, ёмкостной элемент является реактивной нагрузкой.

Выразим электрические величины в комплексной форме. Напряжение и ток (действующие значения) в цепи имеют вид

U = U·ej·ψu, I = I·ej·ψi , ψu = 0, ψi = π/2, φ = — π/2.

Комплексное сопротивление цепи

Ёмкостное сопротивление является отрицательным мнимым числом.

13 цепь синусоидального тока с реальной катушкой индуктивности.

Последовательно соединенные реальная индуктивная катушка и конденсатор в цепи синусоидального тока

Катушка с активным сопротивлением R и индуктивностью L и конденсатор емкостью С включены последовательно(рис.6.8). В схеме протекает синусоидальный ток

Определим напряжение на входе схемы. В соответствии со вторым законом Кирхгофа,

Подставим эти формулы в уравнение (6.15). Получим:

Из выражения (6.16) видно: напряжение в активном сопротивлении совпадает по фазе с током, напряжение на индуктивности опережает по фазе ток на 90o, напряжение по емкости отстает по фазе от тока на 90o. Запишем уравнение (6.16) в комплексной форме:

Поделим левую и правую части уравнения (6.17) на √2. Получим уравнение для комплексов действующих значений токов и напряжений

где — комплексное сопротивление цепи; — модуль комплексного сопротивления, или полное сопротивление цепи; — начальная фаза комплексного сопротивления.

При построении векторных диаграмм цепи рассмотрим три случая.

XL > XC, цепь носит индуктивный характер. Векторы напряжений на индуктивности и емкости направлены в противоположные стороны, частично компенсируют друг друга. Вектор напряжения на входе схемы опережает вектор тока(рис.6.9).
Индуктивное сопротивление меньше емкостного. Вектор напряжения на входе схемы отстает от вектора тока. Цепь носит емкостный характер (рис.6.10).
Индуктивное и емкостное сопротивления одинаковы. Напряжения на индуктивности и емкости полностью компенсируют друг друга. Ток в цепи совпадает по фазе с входным напряжением. В электрической цепи наступает режим резонансного напряжения (рис.6.11).

Ток в резонансном режиме достигает максимума, так как полное сопротивление (z) цепи имеет минимальное значение.

Условие возникновения резонанса: , отсюда резонансная частота равна

Из формулы следует, что режима резонанса можно добиться следующими способами:

изменением частоты;
изменением индуктивности;
изменением емкости.

В резонансном режиме входное напряжение равно падению напряжения в активном сопротивлении. На индуктивности и емкости схемы могут возникнуть напряжения, во много раз превышающие напряжение на входе цепи. Это объясняется тем, что каждое напряжение равно произведению тока I0 (а он наибольший), на соответствующее индуктивное или емкостное сопротивление (а они могут быть большими).

Рис. 6.9 Рис. 6.10 Рис. 6.11

14 цепь синусоидального тока с последовательным соединением активного и емкостного сопротивлений.

15 цепь переменного однофазного тока с последовательным соединением активного, индуктивного и емкостного сопротивлений.