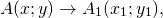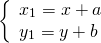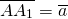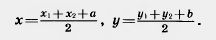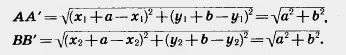Четырехугольник в параллельном переносе (6 видео)

Параллельный перенос

Параллельный перенос — это преобразование плоскости, при котором точки смещаются в одном и том же направлении на одно и то же расстояние.

Строгое определение параллельного переноса даётся либо через декартовы координаты, либо через вектор.

1) Введём на плоскости декартовы координаты x, y.

Параллельный перенос — это такое преобразование фигуры F, при котором её произвольная точка (x;y) переходит в точку (x+a; y+b), где a и b — некоторые числа, одинаковые для всех точек (x;y) фигуры F.

Формулы параллельного переноса

Если при параллельном переносе точка A(x;y) переходит в точку A1(x1;y1)

то параллельный перенос задаётся формулами:

Говорят также, что A1 является образом точки A при параллельном переносе на вектор (a; b). Точка A называется прообразом.

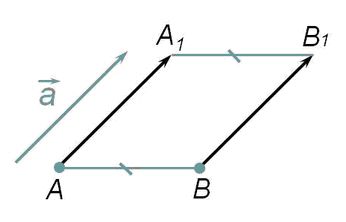
2) Параллельный перенос на данный вектор ā называется отображение плоскости на себя, при котором каждая точка A отображается в такую точку A1, то вектор AA1 равен вектору ā:

Свойства параллельного переноса

1) Параллельный перенос есть движение (то есть параллельный перенос сохраняет расстояние).

2) При параллельном переносе точки смещаются по параллельным (или совпадающим) прямым на одно и то же расстояние.

3) При параллельном переносе каждая прямая переходит в параллельную ей прямую (или в себя).

4) Каковы бы ни были точки A и A1, существует единственный параллельный перенос, при котором точка A переходит в точку A1.

В алгебре параллельный перенос широко используется для построения графиков функций.

Содержание

Четырехугольник в параллельном переносе
Содержание
Общие сведения о параллельном переносе
Свойства параллельного переноса
Повторение темы о параллельном переносе
Свойства, которыми обладает параллельный перенос в пространстве
Истрия и применение в науке
Примеры из жизни
9 класс. Геометрия. Движение. Свойства движения. Параллельный перенос.
9 класс. Геометрия. Движение. Свойства движения. Параллельный перенос.
Вопросы
Поделись с друзьями
Комментарии преподавателя
1. Введение
🌟 Видео

Видео:Геометрия 9 класс (Урок№29 - Параллельный перенос.)Скачать

Четырехугольник в параллельном переносе

Параллельный перенос и его свойства

Видео:Четырехугольник.Параллельный перенос.aviСкачать

Содержание

Видео:8 класс, 3 урок, ЧетырехугольникСкачать

Общие сведения о параллельном переносе

Наглядно параллельный перенос определяется как преобразование, при котором точки смещаются в одном и том же направлении на одно и то же расстояние (рис. 198). Такое определение не является математически строгим, потому что в нем употребляется выражение «в одном и том же направлении», которое само нуждается в точном определении. В связи с этим параллельному переносу мы дадим другое, отвечающее тому же наглядному представлению, но уже строгое определение.

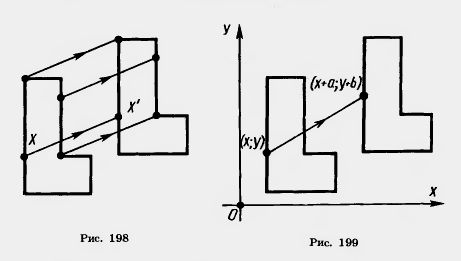
Введем на плоскости декартовы координаты х, у. Преобразование фигуры F, при котором произвольная ее точка (х; у) переходит в точку (х + а; у + b), где а и b одни и те же для всех точек (х; у), называется параллельным переносом (рис. 199). Параллельный перенос задается формулами x’ = x + а, у’ = у + b.

Эти формулы выражают координаты х’, у’ точки, в которую переходит точка (х; у) при параллельном переносе.

Видео:Параллельный перенос точки, отрезка, треугольника, четырехугольника. Геометрия 8 классСкачать

Свойства параллельного переноса

Параллельный перенос есть движение.

Действительно, две произвольные точки А(х₁; у₁) к В (х₂; у₂) переходят при параллельном переносе в точки А’ (х₁ +а; у₁ + b), В'(х₂ + а; y₂+b). Поэтому
АВ 2 =(х₂-х₁) 2 + (у₂-у₁ ) 2

Отсюда АВ=А’В’. Таким образом, параллельный перенос сохраняет расстояния, а значит, является движением, что и требовалось доказать.

Название «параллельный перенос» оправдывается тем, что при параллельном переносе точки смещаются по параллельным (или совпадающим) прямым на одно и то же расстояние.

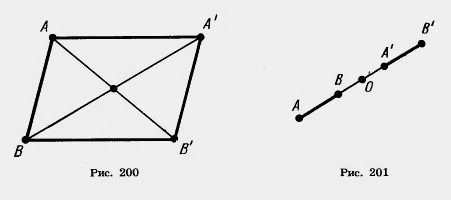
Действительно, пусть точки A (x₁; y₁) и В (x₂; y₂) переходят в точки A'(x₁+а; y₁ + b) и В’ (х₂ + а; y₂ + b) (рис. 200). Середина отрезка АВ’ имеет координаты

Те же координаты имеет и середина отрезка А’В. Отсюда следует, что диагонали четырехугольника АА’В’В пересекаются и точкой пересечения делятся пополам. Значит, этот четырехугольник — параллелограмм. А у параллелограмма противолежащие стороны А А’ и ВВ’ параллельны и равны.

Заметим, что у параллелограмма АА’В’В параллельны и две другие противолежащие стороны — АВ и А ‘В’. Отсюда следует, что при параллельном, переносе прямая переходит в параллельную прямую (или в себя).

Замечание. В предыдущем доказательстве предполагалось, что точка В не лежит на прямой АА’. В случае, когда точка В лежит на прямой АА’, точка В’ тоже лежит на этой прямой, так как середина отрезка АВ’ совпадает с серединой отрезка ВА’ (рис. 201). Значит, все точки А, В, А’, В’ лежат на одной прямой. Далее,

Таким образом, в этом случае точки АиВ смещаются по прямой АВ на одно и то же расстояние 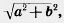а прямая АВ переходит в себя.

Видео:9 класс, 32 урок, Параллельный переносСкачать

Повторение темы о параллельном переносе

Мы с вами уже познакомились с такой темой, как параллельный перенос. На этом уроке вы узнали, что такое преобразование на плоскости, где все точки перемещаются на одно и то же расстояние, считается параллельным переносом.

Из данного урока, каждому из вас стало понятно, что параллельный перенос является движением, так как при таком переносе любая прямая переходит в такую же параллельную ей прямую.

Если мы посмотрим на рисунок, то можем наглядно представить такое движение, как сдвиг площади в направлении данного вектора на его длину.

Видео:11 класс, 12 урок, Параллельный переносСкачать

Свойства, которыми обладает параллельный перенос в пространстве

• Во-первых, параллельный перенос является движением;
• Во-вторых, при выполнении этого действия все точки смещаются по параллельным прямым и притом на одно и то же расстояние;
• В-третьих, при таком переносе прямая имеет свойство переходить в такую же параллельную прямую или в себя саму;
• В-четвертых, независимо от того, какими точками были A и A’, но точка A переходит в точку A’.
• В-пятых, при таком переносе, т.е параллельном переносе в пространстве, в любом случае плоскость имеет свойство переходить в себя саму или же такую же параллельную ей плоскость.

Видео:Параллельный переносСкачать

Истрия и применение в науке

Как правило, в каждого понятия есть свой первооткрыватель, но автор параллельного переноса в пространстве, на жаль, нам неизвестен. А вот применение параллельного переноса в пространстве довольно широко. Как правило, такой перенос используют при преобразовании графической функции в математике, в механике, а также в кристаллографии.

Но если рассматривать трансляция или кристаллографию, то в этом случае перенос приобретает симметричное преобразование, в котором узел пространственной решётки должен совпасть с идентичным ближайшим узлом. В принципе, трансляцию можно отнести к частному случаю параллельного переноса, так как при сдвиге на определенный вектор ее свойства в данной системе не изменяются, а являются вектором трансляции и для нее свойственна трансляционная симметрия.

Видео:Геометрия и группы. Алексей Савватеев. Лекция 2.3. Параллельный переносСкачать

Примеры из жизни

В повседневной жизни мы с вами также постоянно сталкиваемся с примерами параллельного переноса в пространстве. Таким наглядным примером может быть, применяемая в строительной индустрии скользящая опалубка, этот процесс мы можем наблюдать и при перестановке мебели в квартире, да и следы от подошвы нам также напоминают о параллельном переносе в пространстве.

А также, параллельный перенос можно встретить и в таких необычных ситуациях:

А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений

Видео:ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС И ПОВОРОТ 9 класс геометрия АтанасянСкачать

9 класс. Геометрия. Движение. Свойства движения. Параллельный перенос.

Оглавление
Занятия
Обсуждение
О курсе

Вопросы

Задай свой вопрос по этому материалу!

Поделись с друзьями

Комментарии преподавателя

Движение. Свойства движения

Видео:Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

1. Введение

Докажем теорему: при движении отрезок переходит в отрезок.

Расшифруем формулировку теоремы с помощью Рис. 1. Если концы некоторого отрезка MN при движении отобразились в некоторые точки M1 и N1 соответственно, то любая точка Р отрезка MN обязательно перейдет в некоторую точку Р1 отрезка M1N1, и наоборот, в каждую точку Q1 отрезка M1N1 обязательно отобразится некоторая точка Qотрезка MN.

Как видно из рисунка, MN = MР + РN.

Пусть точка Р переходит в некоторую точку Р1′ плоскости. Из определения движения следует равенство длин отрезков MN = M1N1, MР = M1Р1′, РN = Р1’N1. Из этих равенств следует, что M1Р1′, M1Р1’+ Р1’N1 = MР + РN = MN = M1N1, то есть, точка Р1′ принадлежит отрезку M1N1 и совпадает с точкой P1, в противном случае вместо приведенного равенства было бы справедливо неравенство треугольника M1Р1’+ Р1’N1 > M1N1. То есть мы доказали, что при движении любая точка любая точка Р отрезка MN обязательно перейдет в некоторую точку Р1 отрезка M1N1. Вторая часть теоремы (касательно точки Q1) доказывается абсолютно аналогично.

Доказанная теорема справедлива для любых движений!

Теорема: при движении угол переходит в равный ему угол.

Пусть дан ÐАОВ (Рис. 2). И пусть задано некоторое движение, при котором вершина ÐО переходит в точку О1, а точки А и В – соответственно в точки А1 и В1.

Рассмотрим треугольники АОВ и А1О1В1. По условию теоремы, точки А, О и В переходят при движении в точки А1, О1 и В1соответственно. Следовательно, имеет место равенство длин АО = А1О1, ОВ = О1В1 и АВ = А1В1. Таким образом, АОВ = А1О1В1 по трем сторонам. Из равенства треугольников вытекает равенство соответствующих углов О и О1.

Итак, любое движение сохраняет углы.

Из основных свойств движения вытекает масса следствий, в частности то, что любая фигура при движении отображается на равную ей фигуру

Рассмотрим еще один вид движения – параллельный перенос.

Параллельным переносом на некоторый заданный вектор называется такое отображение плоскости на саму себя, при котором каждая точка М плоскости переходит в такую точку М1 той же плоскости, чтобы (Рис. 3).

Докажем, что параллельный перенос является движением.

Рассмотрим произвольный отрезок MN (Рис. 4). Пусть при параллельном переносе точка М перешла в точку М1, а точка N – в точку N1. При этом выполнены условия параллельного переноса: и . Рассмотрим четырехугольник

ММ1N1N. У него две противоположные стороны (MM1 и NN1) равны и параллельны, как это продиктовано условиями параллельного переноса. Следовательно, данный четырехугольник является параллелограммом согласно одному из признаков последнего. Отсюда вытекает, что и другие две стороны (MN и M1N1) параллелограмма имеют равные длины, что и требовалось доказать.

Таким образом, параллельный перенос, действительно, является движением.

Подведем итоги. Мы знакомы уже с тремя видами движений: осевой симметрией, центральной симметрией и параллельным переносом. Мы доказали, что при движении отрезок переходит в отрезок, а угол – в равный ему угол. Кроме того, можно показать, что прямая при движении переходит в прямую и окружность переходит в окружность того же радиуса.