Определение треугольника равных треугольников

Треугольник − это геометрическая фигура, образованная соединением отрезками трех, не лежащих на одной прямой точек .

Эти точки называются вершинами треугольника. Отрезки, соединяющие эти точки называются сторонами треугольника.

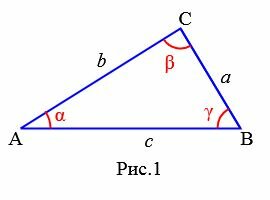Треугольник обозначается знаком ⊿. Например треугольник ABC обозначается так: ⊿ABC. Этот же треугольник можно обозначать так: ⊿BAC, ⊿CBA и т.д.

Углы треугольника обозначают так ∠BAC, ∠ABC, ∠BCA. Эти же углы коротко обозначают также ∠A, ∠B, ∠C, соответственно. Углы треугольника принято также обозначать греческими буквами α, β, γ и т.д. Стороны тркеугольника обозначают так AB, BC, AC. Принято также стороны обозначать одной строчной буквой, причем сторона напротив угла A ,обозначается буквой a, сторона напротив угла B− b, сторона напротив угла C− c. Сумма трех сторон треугольника называется периметром треугольника.

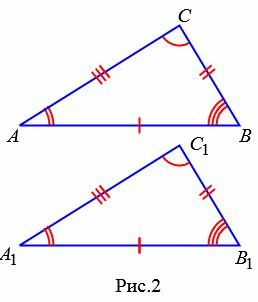
Как известно, две треугольники называются равными, если при наложении друг на друга их можно совместить. На Рис.2 представлены два треугольника ABC и A₁B₁C₁. Треугольник ABC можно наложить на треугольник A₁B₁C₁ так, чтобы вершины и стороны этих треугольников попарно совместились. Очевидно, что при этом совместятся и соответствующие углы.

Вышеизложенное можно сформулировать так:

Если два треугольника равны, то элементы (стороны и углы) одного треугольника соответственно равны элементам другого треугольника. Равенство треугольников ABC и A₁B₁C₁ обозначается так:

Первый признак равенства треугольников

Теорема 1. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то эти треугольники равны.

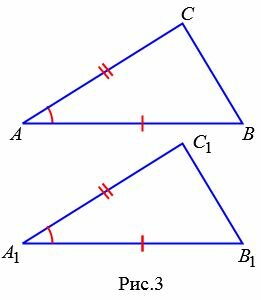Доказательство. Рассмотрим треугольники ABC и A₁B₁C₁ (Рис.3). Пусть AB=A₁B₁, AС=A₁С₁ и ∠A=∠A₁. Докажем, что .

Второй признак равенства треугольников

Теорема 2. Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то эти треугольники равны.

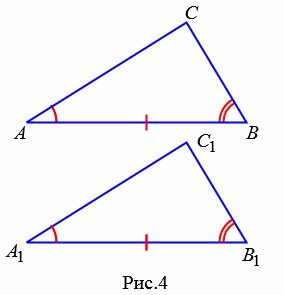Доказательство. Рассмотрим треугольники ABC и A₁B₁С₁ (Рис.4). Пусть AB=A₁B₁, ∠A=∠A₁, ∠B=∠B₁. Докажем, что .

Третий признак равенства треугольников

Теорема 3. Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то эти треугольники равны.

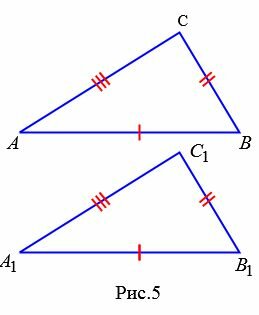Доказательство. Рассмотрим треугольники ABC и A₁B₁С₁. Пусть AB=A₁B₁, AC=A₁C₁ и BC=B₁C₁. Докажем, что . Приложим треугольник ABC к треугольнику A₁B₁С₁ так, чтобы вершина A совмещалась с вершиной A₁, вершина B совмещалась с вершиной B₁, а вершины С и С₁ находились по разные стороны от прямой A₁B₁.

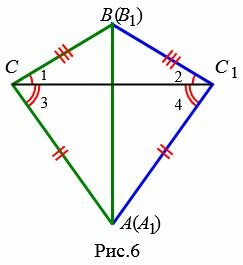Возможны три варианта: луч CC₁ проходит внутри угла ACB(Рис.6); луч CC₁ совпадает с одной из сторон угла ACB (Рис.7); луч CC₁ проходит вне угла ACB(Рис.8). Рассмотрим эти три случая по отдельности.

.

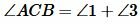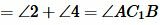Имеем AC=A₁C₁, BC=B₁C₁ ∠ACB=∠A₁C₁B₁ и по первому признаку равенства треугольников . Теорема доказана.

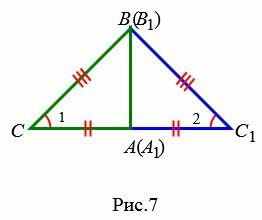Вариант 2 (Рис.7). Так как по условию теоремы AC=A₁C₁ и BC=B₁C₁, то треугольник BСС₁ равнобедренный. Тогда ∠1=∠2. Имеем: AC=A₁C₁, BC=B₁C₁, ∠1=∠2 и по первому признаку равенства треугольников . Теорема доказана.

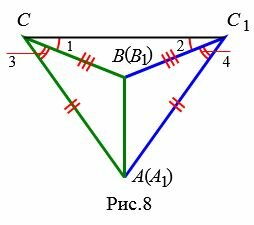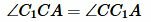
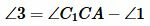Вариант 3 (Рис.8). Так как по условию теоремы AC=A₁C₁ и BC=B₁C₁, то треугольники AСС₁ и BСС₁ равнобедренные. Тогда ∠1=∠2 и и, следовательно:

.

Имеем AC=A₁C₁, BC=B₁C₁ и по первому признаку равенства треугольников . Теорема доказана.

Задачи и решения

Задача 1. На сторонах угла CAD отмечены точки B и E так, что точка B лежит на отрезке AC, а точка E − на отрезке AD, причем AC=AD и AB=AE. Докажите, что ∠CBD=∠DEC (Рис.9).

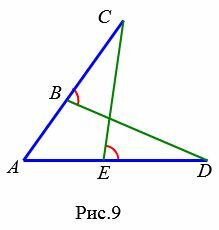Доказательство. AC=AD, AE=AB, ∠CAD общий для треугольников CAE и DAB. Тогда, по первому признаку равенства треугольников (теорема 1) ⊿ACE=⊿ADB. Следовательно ∠DBA=∠AEC. Поскольку углы CBD и DBA смежные, то CBD=180°−∠DBA. Аналогично CED=180°-∠AEC. То есть ∠CBD=∠DEC. Конец доказательства .

Задача 2. По данным рисунка рис.10 докажите, что OP=OT, ∠P=∠T

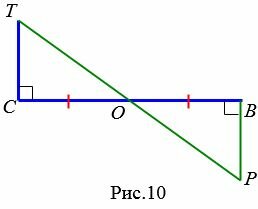Доказательство. OC=OB, ∠TCO=∠PBO=90°. Углы TOC и POB вертикальные (следовательно равны) тогда, повторому признаку равенства треугольников (теорема 2), ⊿TCO=⊿PBO. Конец доказательства .

Равные треугольники

Средняя оценка: 4.5

Всего получено оценок: 312.

Средняя оценка: 4.5

Всего получено оценок: 312.

Изучая тему треугольников, стоит обратить внимание на признаки равенства двух фигур. Их можно использовать во время решений различных заданий. О том, как определить признаки и свойства равенства треугольников – поговорим в этой статье.

Определение

Треугольники ABC и $A_1B_1C_1$ считаются равными в том случае, если их можно совместить наложением. При этом, все стороны и вершины фигур полностью наложатся друг на друга, а все соответствующие углы совместятся.

Исходя из определения равных треугольников, в равных треугольниках все соотвествующие стороны равны и все соответствующие углы равны. Используем это свойство для доказательства признаков равенства треугольников способом наложения.

Для обозначения равенства фигур используют знак “равно”, к примеру, $Δ ABC = Δ А_1В_1С_1$

Математик Фалес, чтобы вычесть расстояние от корабля до суши построил треугольник на суше равный треугольнику на «море». Он, таким образом, узнал точное расстояние.

Признаки равенства

Выделяют три признака равенства треугольников:

1. Если две стороны и угол между ними одного треугольника равны соответствующим двум сторонам и углу между ними другого треугольника, то такие фигуры равны.

Рис. 1. Первый признак равенства

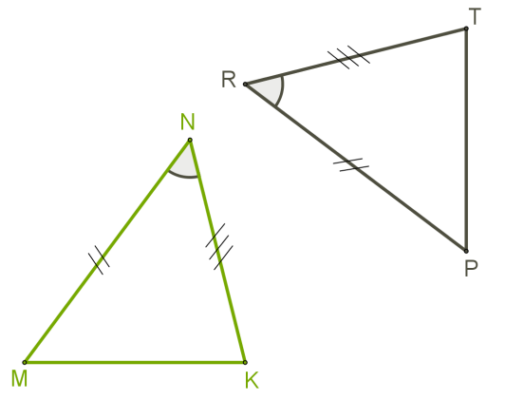
2. Если сторона и два прилегающих к ней угла одного треугольника равны соответствующей стороне и двум прилегающим к ней углам другого треугольника, то такие фигуры равны.

Рис. 2. Второй признак равенства

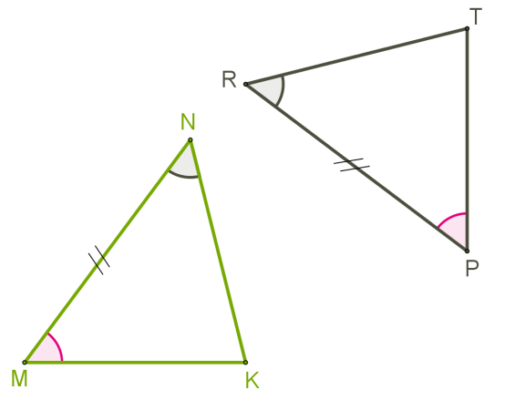
3. Если три стороны в одном треугольнике равны трем сторонам в другом треугольнике, то такие треугольники равны.

Кроме того, стоит выделить некоторые свойства:

• Сумма двух внутренних углов треугольника будет всегда меньше 180 0 .
• Внешний угол треугольника всегда больше внутреннего, при условии, если угол не смежный с ним.
• Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.

Алгоритм доказательства равенства фигур

• Необходимо сориентироваться, для каких треугольников необходимо доказать равенство. Для удобства можно выделить их разными цветами.
• На рисунке отметить, все необходимые данные в условии задания.
• Проверить есть ли у двух треугольников общая сторона либо угол.
• Далее необходимо проанализировать, имеют ли треугольники по две пары равных сторон либо углов. А также необходимо поразмышлять, как можно доказать равенство третьей стороны, либо угла между ними.
• При недостатке данных необходимо выяснить: можно ли использовать равенство других треугольников, чтобы доказать равенство нужных по условию.
• При необходимости, можно сделать дополнительное построение.

Порядок названия вершин одного треугольника должен быть одинаковым с порядком названия вершин другого треугольника.

Стойки стремянки могут свободно раздвигаться, до того момента, когда их не зафиксировали перемычкой. Жесткость такой конструкции основывается на третьем признаке равенства фигур.

Пример

Задание:
Два отрезка пересекаются в точке О и делятся этой точкой пополам. Доказать, что $Δ ABO = Δ CDO$.

Решение:
Стоит обратить внимание на рисунок

Рис. 3. Два треугольника

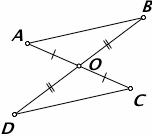
В условии задания сказано, что $BO=OD$, $AO = OС$. А углы $AOB$ и $COD$ равны, так как они вертикальные. Поэтому $Δ ABO = Δ CDO$ по первому признаку равенства треугольников.

Что мы узнали?

Для того, чтобы доказать равенство фигур необходимо использовать один из трех признаков равенства треугольников. Треугольники могут быть равными по двум сторонами и углу между ними, по стороне и двум прилегающим к ней углам, а также по трем сторонам.

math4school.ru

Треугольники

Основные свойства

Треугольник – это геометрическая фигура, которая состоит из трёх точек, не лежащих на одной прямой (вершин треугольника) и трёх отрезков с концами в этих точках (сторон треугольника).

Углами (внутренними углами) треугольника называются три угла, каждый из которых образован тремя лучами, выходящими из вершин треугольника и проходящими через две другие вершины.

Внешним углом треугольника называется угол, смежный внутреннему углы треугольника.

Сумма углов треугольника равна 180°:

Внешний угол равен сумме двух внутренних углов, не смежных с ним, и больше любого внутреннего, с ним не смежного:

Длина каждой стороны треугольника больше разности и меньше суммы длин двух других сторон:

В треугольнике против большего угла лежит большая сторона, против большей стороны лежит больший угол:

Средней линией треугольника называется отрезок, который соединяет середины двух его сторон.

Средняя линия треугольника параллельна одной из его сторон и равна её половине:

Равенство треугольников

Треугольники называются равными, если у них соответствующие стороны равны и соответствующие углы равны:

У равных треугольников все соответствующие элементы равны (стороны, углы, высоты, медианы, биссектрисы, средние линии и т.д.)

В равных треугольниках против равных сторон лежат равные углы, а против равных углов – равные стороны.

Первый признак равенства треугольников.

Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны:

Второй признак равенства треугольников.

Если сторона и прилежащие к ней углы одного треугольника равны соответственно стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны:

Третий признак равенства треугольников.

Если три стороны одного треугольника равны соответственно трём сторонам другого треугольника, то такие треугольники равны:

Подобие треугольников

Подобными называются треугольники, у которых соответствующие стороны пропорциональны.

Коэффициент пропорциональности называется коэффициентом подобия:

Два треугольника подобны, если:

• Два угла одного треугольника равны двум углам другого треугольника.
• Две стороны одного треугольника пропорциональны двум сторонам другого, и углы, образованные этими сторонами, равны.
• Стороны одного треугольника пропорциональны сторонам другого.

У подобных треугольников соответствующие углы равны, а соответствующие отрезки пропорциональны:

Отношение периметров подобных треугольников равно коэффициенту подобия.

Отношение площадей подобных треугольников равно квадрату коэффициента подобия.

Прямая, пересекающая две стороны треугольника, и параллельная третьей, отсекает треугольник, подобный данному:

Три средние линии треугольника делят его на четыре равных треугольника, подобные данному, с коэффициентом подобия ½:

Медианы треугольника

Медианой треугольника называется отрезок, который соединяет вершину треугольника с серединой противолежащей стороны.

Три медианы треугольника пересекаются в одной точке, делящей медианы в отношении 2:1, считая от вершины:

• Медиана делит треугольник на два равновеликих (с равными площадями) треугольника.
• Три медианы треугольника делят его на шесть равновеликих треугольников:

Длины медиан, проведённых к соответствующим сторонам треугольника, равны:

Биссектрисы треугольника

Биссектрисой треугольника, проведённой из данной вершины, называется отрезок биссектрисы угла треугольника, соединяющий эту вершину с точкой на противолежащей стороне.

Биссектрисы внутренних углов треугольника пересекаются в одной точке, находящейся внутри треугольника, равноудалённой от трёх его сторон, которая является центром окружности, вписанной в данный треугольник.

Биссектриса внутреннего угла треугольника делит противолежащую углу сторону на отрезки, пропорциональные двум другим сторонам:

Длина биссектрисы угла А :

Биссектрисы внутреннего и смежного с ним внешнего угла перпендикулярны.

Биссектриса внешнего угла треугольника делит (внешне) противолежащую сторону на отрезки, пропорциональные двум другим сторонам.

BL – биссектриса угла В ;

ВЕ – биссектриса внешнего угла СВК :

Высоты треугольника

Высотой треугольника называется перпендикуляр, опущенный из любой вершины треугольника на противолежащую сторону или на продолжение стороны.

Высоты треугольника пересекаются в одной точке, которая называется ортоцентром треугольника.

Высоты треугольника обратно пропорциональны его сторонам:

Длина высоты, проведённой к стороне а :

Серединные перпендикуляры

Серединный перпендикуляр – это прямая, которая проходит через середину стороны треугольника перпендикулярно к ней.

Три серединных перпендикуляра треугольника пересекаются в одной точке, которая является центром окружности, описанной около данного треугольника.

Точка пересечения биссектрисы угла треугольника с серединным перпендикуляром противолежащей стороны лежит на окружности, описанной около данного треугольника.

Окружность, вписанная в треугольник

Окружность называется вписанной в треугольник, если она касается всех его сторон.

Точки касания вписанной окружности сторон треугольника отсекают от его сторон три пары равных между собой отрезков:

Радиус вписанной в треугольник окружности – расстояние от её центра до сторон треугольника:

Окружность, описанная около треугольника

Окружность называется описанной около треугольника, если она проходит через все его вершины.

Радиус описанной окружности:

Расположение центра описанной окружности

Центр описанной окружности остроугольного треугольника расположен внутри треугольника.Центр описанной окружности прямоугольного треугольника совпадает с серединой его гипотенузы.Центр описанной окружности тупоугольного треугольника расположен вне треугольника.

Равнобедренный треугольник

Треугольник называется равнобедренным, если у него две стороны равны. Равные стороны называют боковыми сторонами, а третью – основанием равнобедренного треугольника.

В равнобедренном треугольнике углы при основании равны: ∠ A = ∠ C.

В равнобедренном треугольнике медиана, проведённая к основанию, является и биссектрисой, и высотой: BL – медиана, биссектриса, высота.

Основные формулы для равнобедренного треугольника:

Равносторонний треугольник

Треугольник у которого все стороны равны называется равносторонним или правильным треугольником.

Центры вписанной и описанной окружностей правильного треугольника совпадают.

Все углы равностороннего треугольника равны:

Каждая медиана равностороннего треугольника совпадает с биссектрисой и высотой, которые проведены из той же вершины:

Основные соотношения для элементов равностороннего треугольника

Прямоугольный треугольник

Треугольник называется прямоугольным, если у него есть прямой угол.

Стороны, прилежащие к прямому углу, называются катетами, противолежащая прямому углу – гипотенузой.

Прямоугольные треугольники равны если у них равны:

• два катета;
• катет и гипотенуза;
• катет и прилежащий острый угол;
• катет и противолежащий острый угол;
• гипотенуза и острый угол.

• одному острому углу;
• из пропорциональности двух катетов;
• из пропорциональности катета и гипотенузы.

Катет прямоугольного треугольника есть среднее пропорциональное между гипотенузой и проекцией этого катета на гипотенузу:

Высота прямоугольного треугольника, проведённая из вершины прямого угла, есть среднее пропорциональное между проекциями катетов на гипотенузу:

Высота прямоугольного треугольника, проведённая из вершины прямого угла, может быть определена через катеты и их проекции на гипотенузу:

Медиана, проведённая из вершины прямого угла, равна половине гипотенузы:

Высота прямоугольного треугольника, проведённая из вершины прямого угла, делит данный треугольник на два треугольника, подобные данному:

Площадь прямоугольного треугольника можно определить

через катеты:

через катет и острый угол:

через гипотенузу и острый угол:

Центр описанной окружности совпадает с серединой гипотенузы.

Радиус описанной окружности:

Радиус вписанной окружности:

Вневписанные окружности

Три окружности, каждая из которых касается одной стороны (снаружи) и продолжений двух других сторон треугольника, называются вневписанными.

Центр вневписанной окружности лежит не пересечении биссектрисы одного внутреннего угла и биссектрис внешних углов при двух других вершинах.

Так точка О₁ , центр одной из вневписанных окружностей Δ ABC , лежит на пересечении биссектрисы ∠ A треугольника ABC и биссектрис BО₁ и C О₁ внешних углов Δ ABC при вершинах B и C .

Таким образом, шесть биссектрис треугольника – три внутренние и три внешние – пересекаются по три в четырёх точках – центрах вписанной и трёх вневписанных окружностей.

Δ ABC является ортоцентричным в Δ О₁О₂О₃ (точки A , B и C – основания высот в Δ О₁О₂О₃ ).

В Δ ABC углы равны 180°–2 О₁ , 180°–2 О₂ , 180°–2 О₃ .

Радиус окружности, описанной около Δ О₁О₂О₃ , равен 2 R , где R – радиус окружности, описанной около Δ ABC .

Δ ABC имеет наименьший периметр среди всех треугольников, вписанных в Δ О₁О₂О₃ .

Если r_a , r_b , r_с – радиусы вневписанных окружностей в Δ ABC , то в Δ ABC верно:

для r –

для R –

для S –

для самих r_a , r_b , r_с –

Теоремы синусов, косинусов, тангенсов; формулы Мольвейде

Теорема косинусов. Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними:

• если c 2 > a 2 +b 2 , то угол γ – тупой ( cos γ
• если c 2 2 +b 2 , то угол γ – острый ( cos γ > 0 );
• если c 2 = a 2 +b 2 , то угол γ – прямой ( cos γ = 0 ).

Теорема синусов. Стороны треугольника пропорциональны синусам противолежащих углов. Коэффициент пропорциональности равен диаметру описанной окружности:

Теорема тангенсов (формула Региомонтана):