Главная > Документ
| Информация о документе | |
| Дата добавления: | |
| Размер: | |
| Доступные форматы для скачивания: |
Разложение вектора по двум неколлинеарным векторам .
При решении задач часто возникает необходимость выразить какой-либо вектор через уже заданные векторы. Такая операция называется разложением вектора по неколлинеарным векторам.
Лемма о коллинеарных векторах.
Лемма — это вспомогательное утверждение, с помощью которого доказывается следующая теорема или несколько теорем.
2) Пусть a и b — два данных вектора. Если вектор р представлен в виде p=xa+yb, где х и у -некоторые числа, то говорят, что вектор р разложен по векторам a и b. Числа х и у называются коэффициентами разложения.
Пример:
пусть надо разложить вектор с(19;-9) по векторам а(-2;3) и в(5;-1)
с=ха+ув
<-2х+5у=19
<3х-у=-9
решив эту систему,получаем х=-2 и у=3
Т.о.,с=-2а+3в
3) 1-Любой вектор р можно разложить,и притом единственным образом,по двум данным неколлинеарным векторам
2-вот как это делается:
1. Каждая координата суммы векторов равна сумме соответствующих координат.
2. Каждая координата разности векторов равна разности соответствующих координат.
3. Каждая координата произведения вектора на число равна произведению соответствующей координаты вектора на это число.
4. Каждая координата вектора равна разности соответствующих координат его конца и начала.
5) Отложим от точки О два единичных вектора, направление которых совпадает с направлениями координатных осей. Эти векторы обозначаются i и j и называются координатными векторами. Так как координатные вектора не коллинеарны, то любой вектор р можно представить в виде p=xi+yj. Числа х и у называются координатами вектора в данной системе координат.
Для координат векторов справедливы следующие свойства:
1. Каждая координата суммы векторов равна сумме соответствующих координат.
2. Каждая координата разности векторов равна разности соответствующих координат.
3. Каждая координата произведения вектора на число равна произведению соответствующей координаты вектора на это число.
4. Каждая координата вектора равна разности соответствующих координат его конца и начала.
6) координаты вектора — э то построение вектора с помщью вспомогательных вектров i и j равными 1, располагаются на координатной плоскости, могут строится от лбо йточки плоскости
Задачи на разложение вектора по двум неколлинеарным векторам задачи
Глава I. Векторы на плоскости и в пространстве
§ 8. Разложение вектора на плоскости по двум неколлинеарным векторам.
Пусть векторы а и b неколлинеарны. Тогда, если числа х и у удовлетворяют условию
В самом деле, если, например, х =/= 0, то из (1) слeдует, что
А это противоречит тому, что векторы а и b неколлинеарны. Таким образом, х = 0.
Аналогично доказывается, что и у = 0.
Теорема. Любой вектор m на плоскости может быть представлен, и притом единственным образом, в виде линейной комбинации двух любых неколлинеарных векторов а и b:
Если вектор т коллинеарен одному из векторов а и b (например, вектору а), то для некоторого числа х имеем
Тем самым вектор т представлен в виде (2).
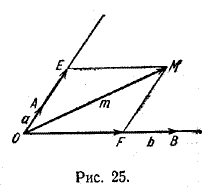
Если же вектор т не коллинеарен ни вектору а, ни вектору b (рис. 25), то, проведя через точку М прямые, параллельные [ОВ) и [ОА), имеем
Но тогда по признаку коллинеарности векторов существуют такие числа х и у, что OE > = ха, OF > = yb, откуда и вытекает равенство (2).
Докажем единственность такого представления. Пусть
Если вектор представлен в виде линейной комбинации каких-то векторов, то говорят, что вектор разложен по этим векторам.
Базисом на плоскости называются два любых неколлинеарных вектора этой плоскости, взятые в определенном порядке.
Пусть e1 и e2 — некоторый базис и а — произвольный вектор, тогда по доказанной теореме существуют два числа х и у такие, что
Числа х и у называются координатами вектора а в данном базисе. В этом случае пишут а = (х; у).
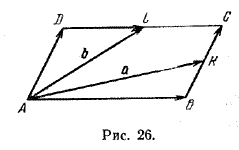
Задача 1. Точки К и L—середины сторон ВС и CD параллелограмма ABCD. Разложить вектор ВС по векторам а = AK > и b = AL > .
Из / АКВ (рис. 26) имеем
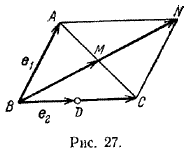
Задача 2. Дан / АВС, D 
[ВС], |BD| = |DC|, [ВМ] — медиана / АВС. Найти координаты вектора ВМ, если направленные отрезки BA > и BD > определяют базисные векторы.
Достроим / АВС до параллелограмма ABCN (рис. 27).
Итак, в данном базисе BM > = ( 1 /2; 1).
Другой вариант решения задачи авторами не рассматривается, хотя он, возможно, проще и нагляднее. Достаточно лишь провести вектор DM > . При этом |DM| — средняя линия / АВС, (что вытекает из условия задачи) и, следовательно, DM > = 1 /2 • BA >
Разложение вектора по двум неколлинеарным векторам
Просмотр содержимого документа
«Разложение вектора по двум неколлинеарным векторам»
ПОВТОРИМ 1. Дайте определение вектора
Длина или модуль ненулевого вектора АB- это .
Ненулевые вектора называются коллинеарными, если…….
Сколько векторов равных данному можно отложить от точки…..
Два коллинеарных вектора направленные одинаково называются ……
Векторы называются равными ,если…..
Разложение вектора по двум неколлинеарным векторам
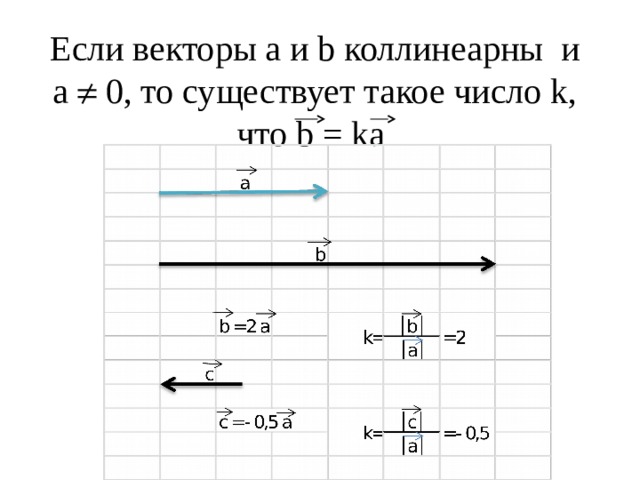
Если векторы а и b коллинеарны и а 0, то существует такое число k, что b = ka
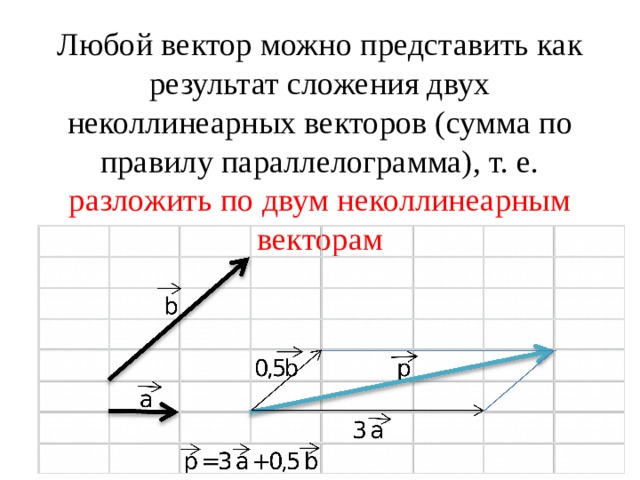
Любой вектор можно представить как результат сложения двух неколлинеарных векторов (сумма по правилу параллелограмма), т. е. разложить по двум неколлинеарным векторам
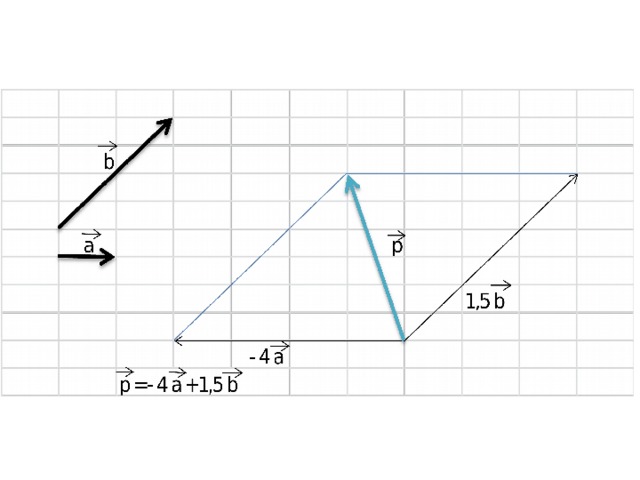
Чтобы разложить вектор по двум векторам надо: 1) отложить все три вектора от одной точки; 2) достроить до параллелограмма; 3) вычислить значения k для каждого вектора
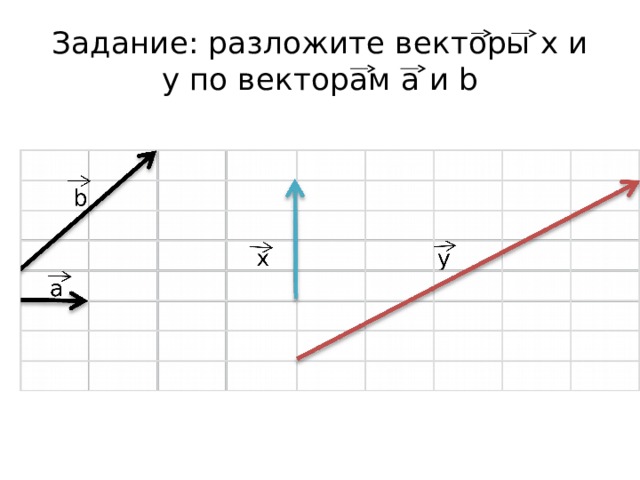
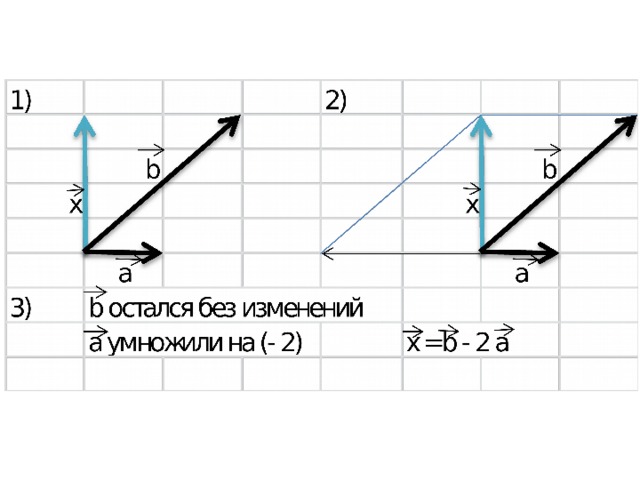
Задание: разложите векторы x и y по векторам a и b
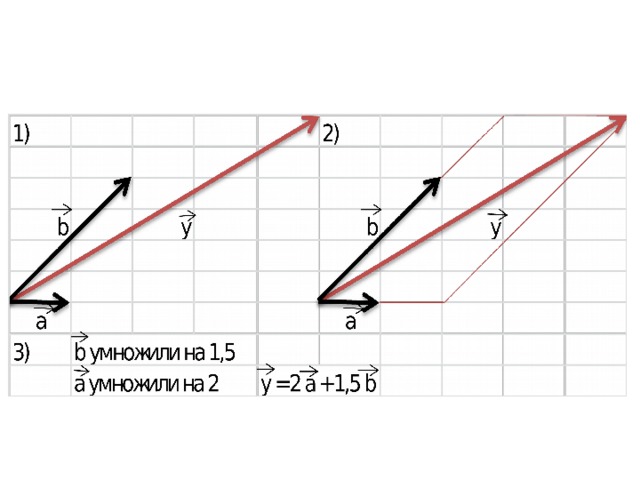
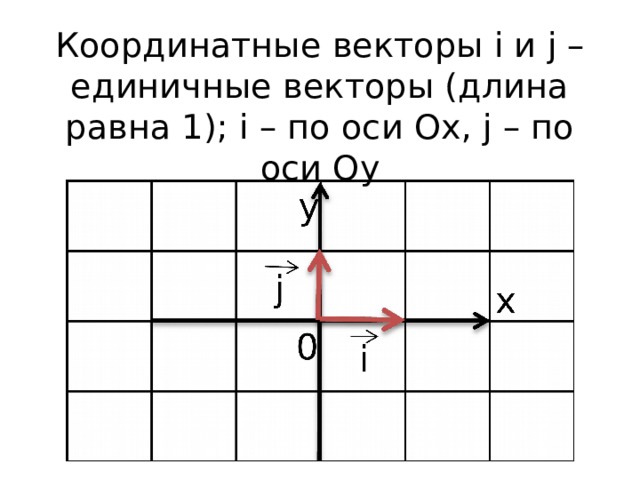
Координатные векторы i и j – единичные векторы (длина равна 1); i – по оси Ox, j – по оси Oy
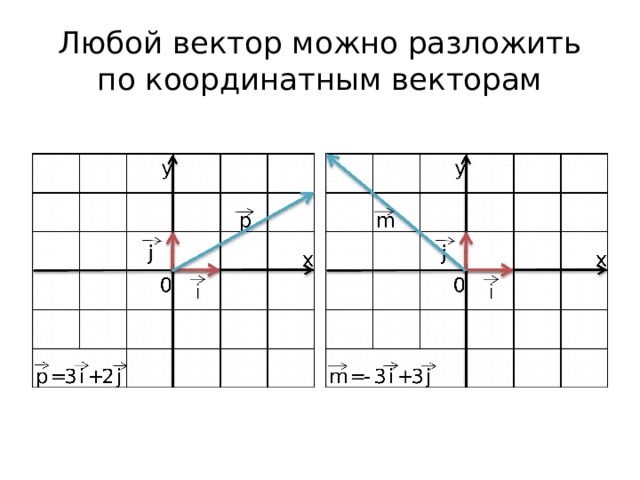
Любой вектор можно разложить по координатным векторам
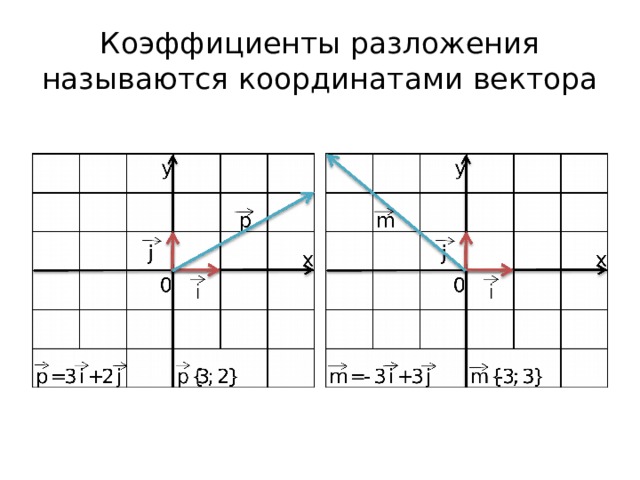
Коэффициенты разложения называются координатами вектора
1. Каждая координата суммы векторов равна сумме соответствующих координат a + b = c 2. Каждая координата разности векторов равна разности соответствующих координат a — b = c
3. Каждая координата произведения вектора на число равна произведению соответствующей координаты на это число если a , то -4 a
Задание: найти координаты вектора p = 2 a – 1/3 b + c , если a , b , c 1) 2a , 2a 2) – 1/3b , — 1/3 b 3) c 4) p , p