Хорда — отрезок соединяющий любые две точки окружности. Диаметр окружности, самая большая хорда.
L — хорда
R — радиус окружности
O — центр окружности
α — центральный угол
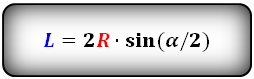
Формула длины хорды, ( L ):
Калькулятор для расчета длины хорды окружности :
Дополнительные формулы для окружности:
- Как найти хорду окружности в цилиндре
- Определение хорды
- Свойства хорды к окружности
- Свойства хорды и вписанного угла
- Свойства хорды и центрального угла
- Формулы нахождения хорды
- Решение задач
- Как найти хорду окружности в цилиндре
- Как найти хорду окружности?
- Окружность. Длина окружности. Касательная, дуга
- Касательная к окружности
- Углы в окружности
- Вписанная окружность
- Описанная окружность
- Теорема Птолемея
- Отрезки и прямые, связанные с окружностью. Теорема о бабочке
- Отрезки и прямые, связанные с окружностью
- Свойства хорд и дуг окружности
- Теоремы о длинах хорд, касательных и секущих
- Доказательства теорем о длинах хорд, касательных и секущих
- Теорема о бабочке
- 💥 Видео
Видео:ОГЭ ЗАДАНИЕ 16 НАЙДИТЕ ДЛИНУ ХОРДЫ ОКРУЖНОСТИ ЕСЛИ РАДИУС 13 РАССТОЯНИЕ ДО ХОРДЫ 5Скачать

Как найти хорду окружности в цилиндре
| Учебный курс | Решаем задачи по геометрии |
Видео:Окружность, диаметр, хорда геометрия 7 классСкачать  Определение хорды
Часть кривой, заключенной между двумя точками хорды, называется дугой. Плоская фигура, заключенная между дугой и ее хордой называется сегментом. Хорда, проходящая через центр окружности, называется диаметром окружности. Диаметр окружности — самая длинная хорда окружности. Видео:ЕГЭ-2022 ||Задание №6 || Найти длину хордыСкачать  Свойства хорды к окружности
Видео:Геометрия 8 класс (Урок№28 - Свойства хорд окружности.)Скачать  Свойства хорды и вписанного углаВидео:Длина хорды окружности равна 72 ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать  Свойства хорды и центрального углаВидео:Длина окружности. Площадь круга - математика 6 классСкачать  Формулы нахождения хорды
Длина хорды окружности равна удвоенному радиусу данной окружности, умноженному на синус половины центрального угла. Видео:Радиус и диаметрСкачать  Решение задачПримечание. Если Вы не нашли решение подходящей задачи, пишите об этом в форуме. Наверняка, курс геометрии будет дополнен.
Решение. Согласно свойству хорд AS x SB = CS x SD, тогда 2х * 3х = 5 * 12 Откуда
Решение. 3,5х + 5,5х + 3х = 360 Откуда градусные величины центральных углов равны: 90 / 2 = 45 Ответ: Величина углов треугольника равна 45 ; 52,5 ; 82,5 ; Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать  Как найти хорду окружности в цилиндреВидео:Демо ОГЭ по математике. Задание 17. Хорда окружности.Скачать  Как найти хорду окружности?Окружность — это множество точек, которое располагается на одинаковом расстоянии от ее центра, представленного точкой. Для любой точки L, лежащей на окружности, действует равенство OL=R. (Длина отрезка OL равняется радиусу окружности). Видео:Круг. Окружность | Математика 3 класс #21 | ИнфоурокСкачать  Окружность. Длина окружности. Касательная, дугаОтрезок, который соединяет две точки окружности, является ее хордой. Хорда, проходящая прямо через центр окружности, является диаметром этой окружности (D). Диаметр можно вычислить по формуле: D=2R Длина окружности вычисляется по формуле: C=2pi R Площадь круга: S=pi R^ Дугой окружности называется та ее часть, которая располагается между двух ее точек. Эти две точки и определяют две дуги окружности. Хорда CD стягивает две дуги: CMD и CLD. Одинаковые хорды стягивают одинаковые дуги. Центральным углом называется такой угол, который находится между двух радиусов. Длину дуги можно найти по формуле:
> > Диаметр, что перпендикулярен хорде, делит хорду и стянутые ею дуги пополам. В случае, если хорды AB и CD окружности имеют пересечение в точке N, то произведения отрезков хорд, разделенные точкой N, равны между собой. Касательная к окружностиКасательной к окружности принято называть прямую, у которой имеется одна общая точка с окружностью. Если же у прямой есть две общие точки, ее называют секущей. Если провести радиус в точку касания, он будет перпендикулярен касательной к окружности. Проведем две касательные из этой точки к нашей окружности. Получится, что отрезки касательных сравняются один с другим, а центр окружности расположится на биссектрисе угла с вершиной в этой точке. Теперь к окружности из нашей точки проведем касательную и секущую. Получим, что квадрат длины отрезка касательной будет равен произведению всего отрезка секущей на его внешнюю часть. Можно сделать вывод: произведение целого отрезка первой секущей на его внешнюю часть равняется произведению целого отрезка второй секущей на его внешнюю часть. Углы в окружностиГрадусные меры центрального угла и дуги, на которую тот опирается, равны. Вписанный угол — это угол, вершина которого находится на окружности, а стороны содержат хорды. Вычислить его можно, узнав величину дуги, так как он равен половине этой дуги. Опирающийся на диаметр, вписанный угол, прямой. angle CBD = angle CED = angle CAD = 90^ Вписанные углы, которые опираются на одну дугу, тождественны. angle ADB = angle AEB = angle AFB Опирающиеся на одну хорду вписанные углы тождественны или их сумма равняется 180^ . angle ADB + angle AKB = 180^ angle ADB = angle AEB = angle AFB На одной окружности находятся вершины треугольников с тождественными углами и заданным основанием. Угол с вершиной внутри окружности и расположенный между двумя хордами тождественен половине суммы угловых величин дуг окружности, которые заключаются внутри данного и вертикального углов. angle DMC = angle ADM + angle DAM = frac left ( cup DmC + cup AlB ight ) Угол с вершиной вне окружности и расположенный между двумя секущими тождественен половине разности угловых величин дуг окружности, которые заключаются внутри угла. angle M = angle CBD — angle ACB = frac left ( cup DmC — cup AlB ight ) Вписанная окружностьВписанная окружность — это окружность, касающаяся сторон многоугольника. В точке, где пересекаются биссектрисы углов многоугольника, располагается ее центр. Окружность может быть вписанной не в каждый многоугольник. Площадь многоугольника с вписанной окружностью находится по формуле: p — полупериметр многоугольника, r — радиус вписанной окружности. Отсюда следует, что радиус вписанной окружности равен: Суммы длин противоположных сторон будут тождественны, если окружность вписана в выпуклый четырехугольник. И наоборот: в выпуклый четырехугольник вписывается окружность, если в нем суммы длин противоположных сторон тождественны. В любой из треугольников возможно вписать окружность. Только одну единственную. В точке, где пересекаются биссектрисы внутренних углов фигуры, будет лежать центр этой вписанной окружности. Радиус вписанной окружности вычисляется по формуле: Описанная окружностьЕсли окружность проходит через каждую вершину многоугольника, то такую окружность принято называть описанной около многоугольника. В точке пересечения серединных перпендикуляров сторон этой фигуры будет находиться центр описанной окружности. Радиус можно найти, вычислив его как радиус окружности, которая описана около треугольника, определенного любыми 3-мя вершинами многоугольника. Есть следующее условие: окружность возможно описать около четырехугольника только, если сумма его противоположных углов равна 180^ . angle A + angle C = angle B + angle D = 180^ Около любого треугольника можно описать окружность, причем одну-единственную. Центр такой окружности будет расположен в точке, где пересекаются серединные перпендикуляры сторон треугольника. Радиус описанной окружности можно вычислить по формулам:
Теорема ПтолемеяПод конец, рассмотрим теорему Птолемея. Теорема Птолемея гласит, что произведение диагоналей тождественно сумме произведений противоположных сторон вписанного четырехугольника. Видео:Расчет сегмента окружности по хорде и длине цилиндрической поверхности (трансцендентное уравнение)Скачать  Отрезки и прямые, связанные с окружностью. Теорема о бабочке
Видео:Окружность и круг, 6 классСкачать  Отрезки и прямые, связанные с окружностьюМножество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности Конечная часть плоскости, ограниченная окружностью Отрезок, соединяющий центр окружности с любой точкой окружности Отрезок, соединяющий две любые точки окружности Хорда, проходящая через центр окружности. Диаметр является самой длинной хордой окружности Прямая, имеющая с окружностью только одну общую точку. Касательная перпендикулярна к радиусу окружности, проведённому в точку касания Прямая, пересекающая окружность в двух точках Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности | ||||||||||||||||||||||
| Круг | ||||||||||||||||||||||
 Конечная часть плоскости, ограниченная окружностью | ||||||||||||||||||||||
| Радиус | ||||||||||||||||||||||
 Отрезок, соединяющий центр окружности с любой точкой окружности | ||||||||||||||||||||||
| Хорда | ||||||||||||||||||||||
 Отрезок, соединяющий две любые точки окружности | ||||||||||||||||||||||
| Диаметр | ||||||||||||||||||||||
 Хорда, проходящая через центр окружности. Диаметр является самой длинной хордой окружности | ||||||||||||||||||||||
| Касательная | ||||||||||||||||||||||
 Прямая, имеющая с окружностью только одну общую точку. Касательная перпендикулярна к радиусу окружности, проведённому в точку касания | ||||||||||||||||||||||
| Секущая | ||||||||||||||||||||||
 Прямая, пересекающая окружность в двух точках Видео:Окружность. Длина хорды. Теорема синусов.Скачать  Свойства хорд и дуг окружности
Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам. | ||||||||||||||||||||||
| Диаметр, проходящий через середину хорды | ||||||||||||||||||||||
 Диаметр, проходящий через середину хорды, перпендикулярен к этой хорде и делит стягиваемые ею две дуги пополам. | ||||||||||||||||||||||
| Равные хорды | ||||||||||||||||||||||
 Если хорды равны, то они находятся на одном и том же расстоянии от центра окружности. | ||||||||||||||||||||||
| Хорды, равноудалённые от центра окружности | ||||||||||||||||||||||
 Если хорды равноудалены (находятся на одном и том же расстоянии) от центра окружности, то они равны. | ||||||||||||||||||||||
| Две хорды разной длины | ||||||||||||||||||||||
 Большая из двух хорд расположена ближе к центру окружности. | ||||||||||||||||||||||
| Равные дуги | ||||||||||||||||||||||
 У равных дуг равны и хорды. | ||||||||||||||||||||||
| Параллельные хорды | ||||||||||||||||||||||
 Дуги, заключённые между параллельными хордами, равны. Видео:Радиус Хорда ДиаметрСкачать  Теоремы о длинах хорд, касательных и секущихПроизведения длин отрезков, на которые разбита каждая из хорд, равны: Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны. Произведения длин отрезков, на которые разбита каждая из хорд, равны: Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны. Произведения длин отрезков, на которые разбита каждая из хорд, равны: Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны. Видео:Длина окружности. Математика 6 класс.Скачать  Доказательства теорем о длинах хорд, касательных и секущихТеорема 1 . Предположим, что хорды окружности AB и CD пересекаются в точке E (рис.1). Тогда справедливо равенство Доказательство . Заметим, что углы BCD и BAD равны как вписанные углы, опирающиеся на одну и ту же дугу. Углы BEC и AED равны как вертикальные. Поэтому треугольники BEC и AED подобны. Следовательно, справедливо равенство откуда и вытекает требуемое утверждение. Теорема 2 . Предположим, что из точки A , лежащей вне круга, к окружности проведены касательная AB и секущая AD (рис.2). Точка B – точка касания с окружностью, точка C – вторая точка пересечения прямой AD с окружностью. Тогда справедливо равенство Доказательство . Заметим, что угол ABC образован касательной AB и хордой BC , проходящей через точку касания B . Поэтому величина угла ABC равна половине угловой величины дуги BC . Поскольку угол BDC является вписанным углом, то величина угла BDC также равна половине угловой величины дуги BC . Следовательно, треугольники ABC и ABD подобны (угол A является общим, углы ABC и BDA равны). Поэтому справедливо равенство откуда и вытекает требуемое утверждение. Теорема 3 . Предположим, что из точки A , лежащей вне круга, к окружности проведены секущие AD и AF (рис.3). Точки C и E – вторые точки пересечения секущих с окружностью. Тогда справедливо равенство Доказательство . Проведём из точки A касательную AB к окружности (рис. 4). Точка B – точка касания. В силу теоремы 2 справедливы равенства откуда и вытекает требуемое утверждение. Видео:Как найти координаты точек на тригонометрической окружностиСкачать  Теорема о бабочкеТеорема о бабочке . Через середину G хорды EF некоторой окружности проведены две произвольные хорды AB и CD этой окружности. Точки K и L – точки пересечения хорд AC и BD с хордой EF соответственно (рис.5). Тогда отрезки GK и GL равны. Доказательство . Существует много доказательств этой теоремы. Изложим доказательство, основанное на теореме синусов, которое, на наш взгляд, является наиболее наглядным. Для этого заметим сначала, что вписанные углы A и D равны, поскольку опираются на одну и ту же дугу. По той же причине равны и вписанные углы C и B . Теперь введём следующие обозначения: Воспользовавшись теоремой синусов, применённой к треугольнику CKG , получим Воспользовавшись теоремой синусов, применённой к треугольнику AKG , получим Воспользовавшись теоремой 1, получим Воспользовавшись равенствами (1) и (2), получим Проводя совершенно аналогичные рассуждения для треугольников BGL и DGL , получим равенство откуда вытекает равенство что и завершает доказательство теоремы о бабочке. 💥 ВидеоОкружность. Круг. 5 класс.Скачать  ВАЖНЫЕ УГЛЫ в Геометрии — Центральный и Вписанный УголСкачать  Задача на нахождение длины хорды окружностиСкачать  Деление окружности на 3; 6; 12 равных частейСкачать  |

















 Отрезки и прямые, связанные с окружностью
Отрезки и прямые, связанные с окружностью

































