Если в четырехугольнике две стороны параллельны то это параллелограмм верно (7 видео)

Если стороны четырехугольника параллельны и равны

Теорема (2-й признак параллелограмма).

Если две стороны четырехугольника параллельны и равны, то этот четырехугольник — параллелограмм.

Дано: ABCD — четырехугольник,

Доказать: ABCD — параллелограмм.

1. Проведем диагональ AC.

2. Рассмотрим треугольники ABC и CDA (важно правильно назвать треугольники!)

1) AD=BC (по условию)

2) сторона AC — общая

3)∠CAD=∠ACB (как внутренние накрест лежащие углы при AD ∥ BC и секущей AC)

Следовательно, треугольники ABC и CDA равны (по двум сторонам и углу между ними).

3. Из равенства треугольников следует равенство соответствующих углов: ∠ACD=∠CAB.

А так как эти углы — внутренние накрест лежащие при прямых AB и CD и секущей AC, то эти прямые параллельны:

4. В четырехугольнике ABCD:

1) AD ∥ BC (по условию)

2) AB ∥ CD (по доказанному).

Следовательно, ABCD — параллелограмм (по определению).

Содержание

Параллелограмм: свойства и признаки
Определение параллелограмма
Свойства параллелограмма
Признаки параллелограмма
Признаки параллелограмма
Доказательство:
Доказательство:
Доказательство:
💥 Видео

Видео:Геометрия Признак параллелограмма: Если в четырех угольнике каждые две противолежащие стороны равныСкачать

Параллелограмм: свойства и признаки

О чем эта статья:

Видео:Геометрия Признак параллелограмма: Если в четырехугольнике противолежащие стороны равныСкачать

Определение параллелограмма

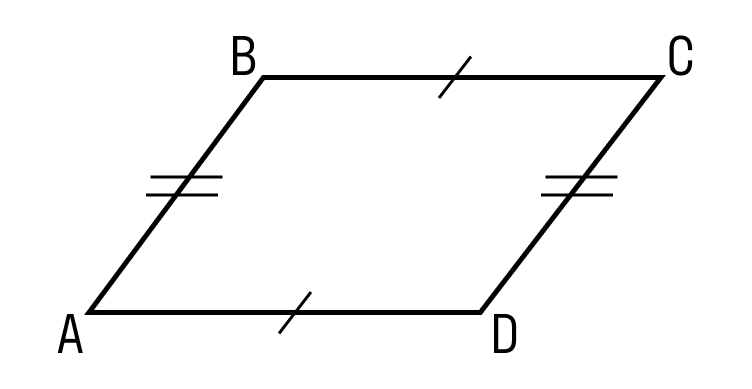
Параллелограмм — это четырехугольник, у которого противоположные стороны попарно параллельны и равны. Как выглядит параллелограмм:

Частные случаи параллелограмма: ромб, прямоугольник, квадрат.

Диагонали — отрезки, которые соединяют противоположные вершины.

Свойства диагоналей параллелограмма:

В параллелограмме точка пересечения диагоналей делит их пополам.
Любая диагональ параллелограмма делит его на два равных треугольника.
Сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его двух смежных сторон.

Биссектриса угла параллелограмма — это отрезок, который соединяет вершину с точкой на одной из двух противоположных сторон и делит угол при вершине пополам.

Свойства биссектрисы параллелограмма:

Биссектриса параллелограмма отсекает от него равнобедренный треугольник.
Биссектрисы углов, прилежащих к одной стороне параллелограмма пересекаются под прямым углом.
Отрезки биссектрис противоположных углов равны и параллельны.

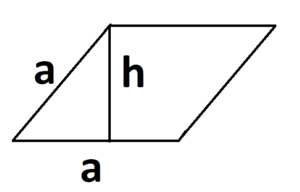
Как найти площадь параллелограмма:

S = a × h, где a — сторона, h — высота.
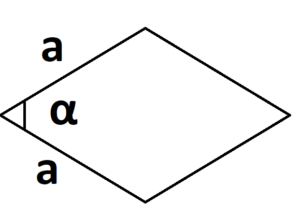
S = a × b × sinα, где a и b — две стороны, sinα — синус угла между ними. Для ромба формула примет вид S = a 2 × sinα.
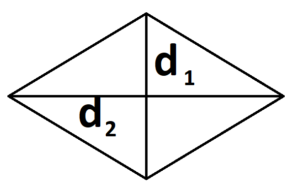
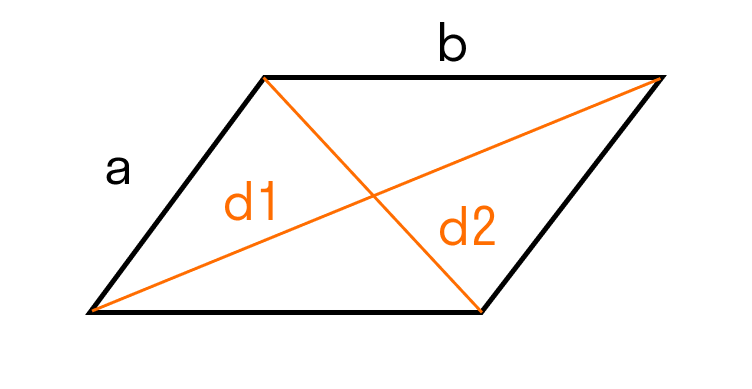
Для ромба: S = 0,5 × (d1 × d2), где d1 и d2 — две диагонали.
Для параллелограмма: S = 0,5 × (d1 × d2) × sinβ, где β — угол между диагоналями.

Периметр параллелограмма — сумма длины и ширины, умноженная на два.

P = 2 × (a + b), где a — ширина, b — высота.

У нас есть отличные дополнительные курсы по математике для учеников с 1 по 11 классы!

Видео:Все про ПАРАЛЛЕЛОГРАММ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // ГеометрияСкачать

Свойства параллелограмма

Геометрическая фигура — это любое множество точек. У каждой фигуры есть свои свойства, которые отличают их между собой и помогают решать задачи по геометрии в 8 классе.

Рассмотрим основные свойства диагоналей и углов параллелограмма, узнаем чему равна сумма углов параллелограмма и другие особенности этой фигуры. Вот они:

Противоположные стороны параллелограмма равны.
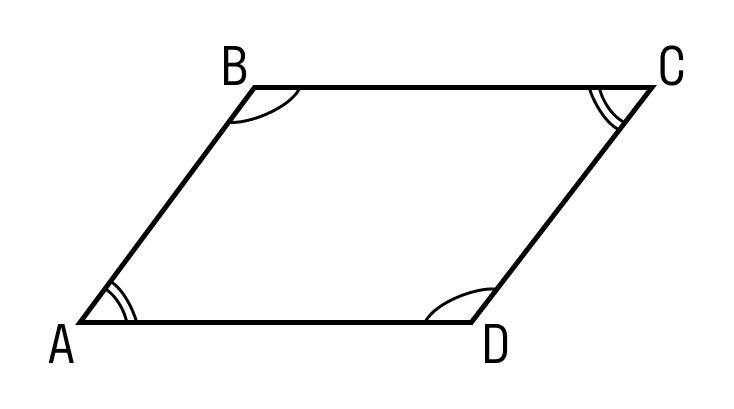
ABCD — параллелограмм, значит, AB = DC, BC = AD.
Противоположные углы параллелограмма равны.
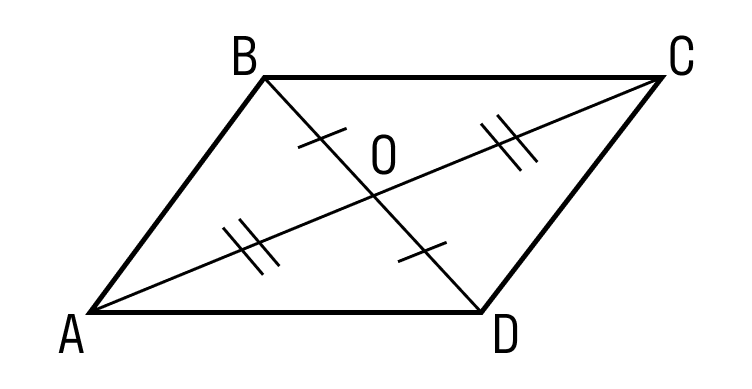
ABCD — параллелограмм, значит, ∠A = ∠C, ∠B = ∠D.
Диагонали параллелограмма точкой пересечения делятся пополам.
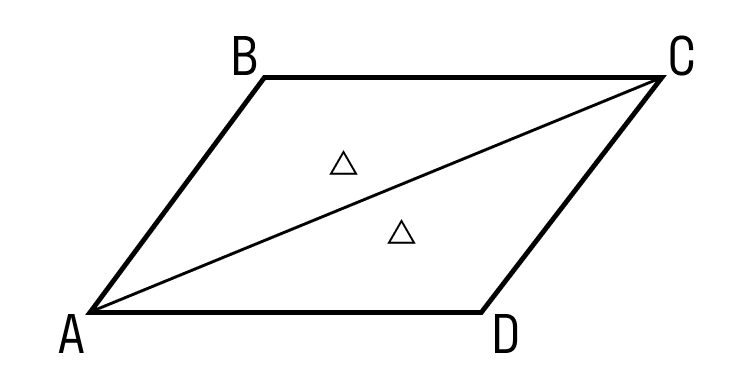
ABCD — параллелограмм, AC и BD — диагонали, AC∩BD=O, значит, BO = OD, AO = OC.
Диагональ делит параллелограмм на два равных треугольника.
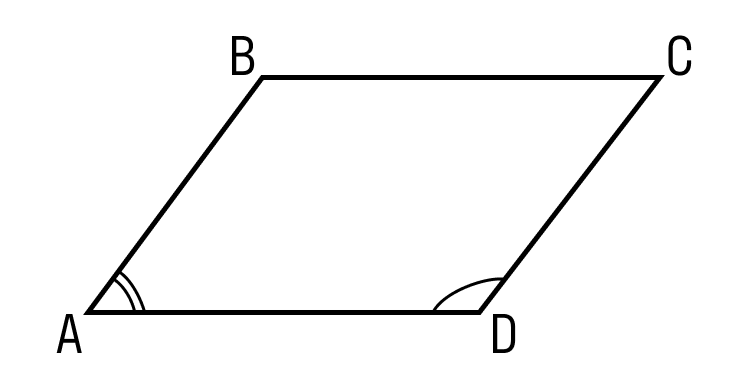
ABCD — параллелограмм, AC — диагональ, значит, △ABC = △CDA.
Сумма углов в параллелограмме, прилежащих к одной стороне, равна 180 градусам.
ABCD — параллелограмм, значит, ∠A + ∠D = 180°.
В параллелограмме диагонали d1, d2 и стороны a, b связаны следующим соотношением: d1 2 + d2 2 = 2 × (a 2 + b 2 ).

А сейчас докажем теорему, которая основана на первых двух свойствах.

Теорема 1. В параллелограмме противоположные стороны и противоположные углы равны.

В любом выпуклом четырехугольнике диагонали пересекаются. Все, что мы знаем о точке их пересечения — это то, что она лежит внутри четырехугольника.

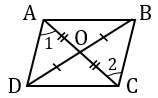
Если мы проведем обе диагонали в параллелограмме, точка пересечения разделит их пополам. Убедимся, так ли это:

AB = CD как противоположные стороны параллелограмма.
∠1 = ∠2 как накрест лежащие углы при пересечении секущей AC параллельных прямых AB и CD; ∠3 = ∠4 как накрест лежащие углы при пересечении секущей BD параллельных прямых AB и CD.
Следовательно, треугольник AOB равен треугольнику COD по второму признаку равенства треугольников, то есть по стороне и прилежащим к ней углам, из чего следует:
- CO = AO
- BO = DO

Теорема доказана. Наше предположение верно.

Видео:Геометрия Признак параллелограмма: Если в четырехугольнике диагонали точкой пересечения делятсяСкачать

Признаки параллелограмма

Признаки параллелограмма помогают распознать эту фигуру среди других четырехугольников. Сформулируем три основных признака.

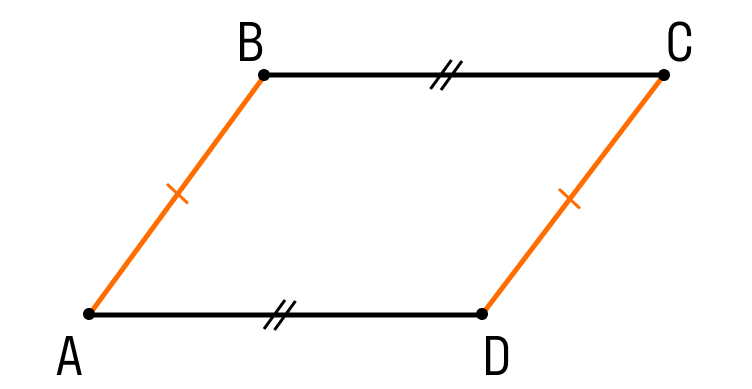
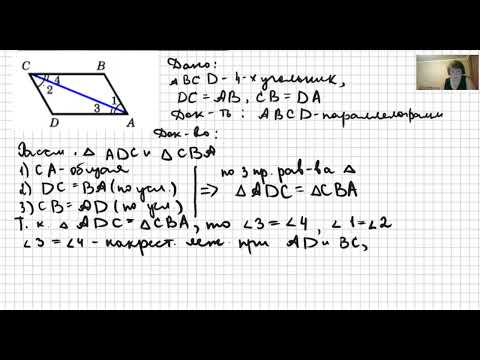
Первый признак параллелограмма. Если в четырехугольнике две противолежащие стороны равны и параллельны, то этот четырехугольник — параллелограмм.

Докажем 1 признак параллелограмма:

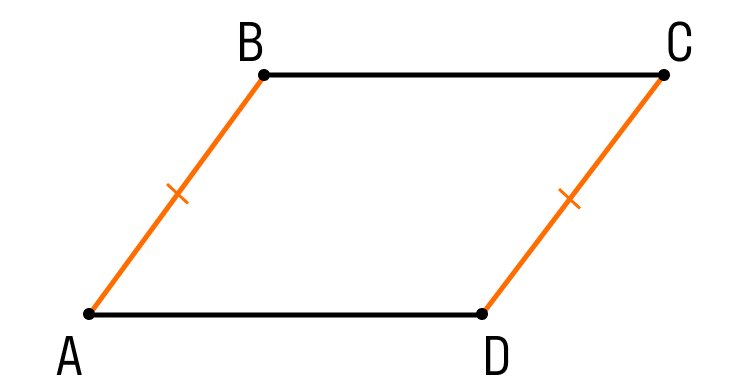
Шаг 1. Пусть в четырехугольнике ABCD:

AB || CD
AB = CD

Чтобы назвать этот четырехугольник параллелограммом, нужно внимательно рассмотреть его стороны.

Сейчас мы видим одну пару параллельных сторон. Нужно доказать, что вторая пара сторон тоже параллельна.

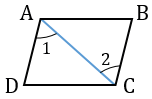
Шаг 2. Проведем диагональ. Получились два треугольника ABC и CDA, которые равны по первому признаку равенства, то есть по по двум сторонам и углу между ними:

AC — общая сторона;
По условию AB = CD;
∠1 = ∠2 как внутренние накрест лежащие углы при пересечении параллельных прямых AB и CD секущей АС.

Шаг 3. Из равенства треугольников также следует:

Эти углы тоже являются внутренними накрест лежащими для прямых CB и AD. А это как раз и есть признак параллельности прямых. Значит, CB || AD и ABCD — параллелограмм.

Вот так быстро мы доказали первый признак.

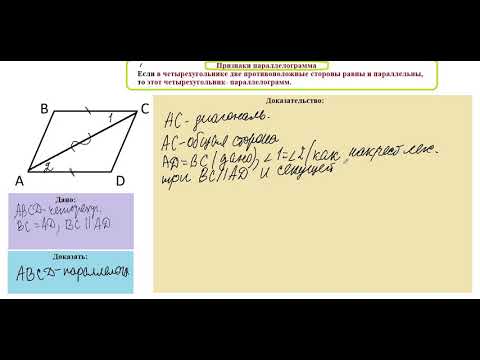
Второй признак параллелограмма. Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник — параллелограмм.

Докажем 2 признак параллелограмма:

Шаг 1. Пусть в четырехугольнике ABCD:

AB = CD
BC = AD

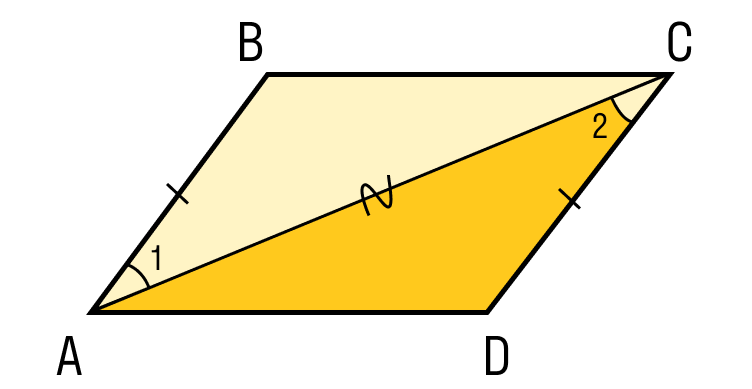
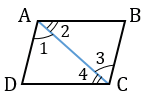
Шаг 2. Проведем диагональ AC и рассмотрим треугольники ABC и CDA:

AC — общая сторона;
AB = CD по условию;
BC = AD по условию.

Из этого следует, что треугольники ABC и CDA равны по третьему признаку, а именно по трем сторонам.

Шаг 3. Из равенства треугольников следует:

А так как эти углы — накрест лежащие при сторонах BC и AD и диагонали AC, значит, стороны BC и AD параллельны.

Эти углы — накрест лежащие при сторонах AB и CD и секущей AC. Поэтому стороны AB и CD тоже параллельны. Значит, четырехугольник ABCD — параллелограмм, ЧТД.

Доказали второй признак.

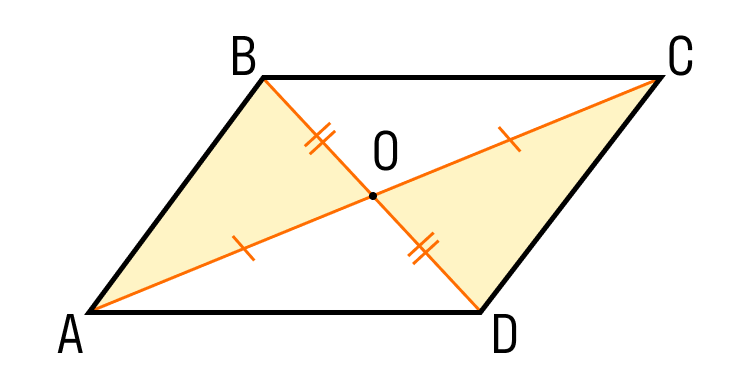
Третий признак параллелограмма. Если в четырехугольнике диагонали точкой пересечения делятся пополам, то этот четырехугольник — параллелограмм.

Докажем 3 признак параллелограмма:

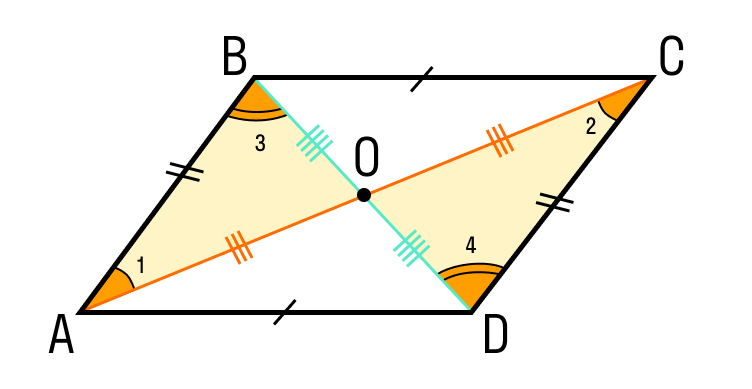
Шаг 1. Если диагонали четырехугольника ABCD делятся пополам точкой O, то треугольник AOB равен треугольнику COD по двум сторонам и углу между ними:

CO = OA;
DO = BO;
углы между ними равны, как вертикальные, то есть угол AOB равен углу COD.

Шаг 2. Из равенства треугольников следует, что CD = AB.

Эти стороны параллельны CD || AB, по равенству накрест лежащих углов: ∠1 = ∠2 (следует из равенства треугольников AOB и COD).

Значит, ABCD является параллелограммом по первому признаку, который мы доказали ранее. Что и требовалось доказать.

Теперь мы знаем свойства параллелограмма и то, что выделяет его среди других четырехугольников — признаки. Так как они совпадают, эти формулировки можно использовать для определения параллелограмма. Но самое распространенное определение все-таки связано с параллельностью противоположных сторон.

Видео:8 класс, 5 урок, Признаки параллелограммаСкачать

Признаки параллелограмма

1 0 . Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник — параллелограмм.

Доказательство:

Дано: АВСD — четырехугольник, АD = ВС, АDВС.

Доказать: АВСD — параллелограмм.

Доказательство:

1. Проведем диагональ АС четырехугольника АВСD.

2. Рассмотрим АВС и АDС: АС — общая, 1 =3 (т.к. по условию АDВС, 1 и 3 накрест лежащие углы при пересечении параллельных прямых АD и BC секущей АС), АВС =АDС (по 1 признаку равенства треугольников), АВ = DC и 2 = 4. Но 2 и 4 накрест лежащие углы при пересечении прямых АВ и DС секущей АС, АВDС.

3. Итак, АDВС и АВDС, т.е. в четырехугольнике АВСD противоположные стороны попарно параллельны, четырехугольник АВСD — параллелограмм. Что и требовалось доказать.

2 0 . Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник — параллелограмм.

Доказательство:

Дано: АВСD — четырехугольник, АВ = DС, АD = ВC.

Доказать: АВСD — параллелограмм.

Доказательство:

1. Проведем диагональ АС четырехугольника АВСD.

2. Рассмотрим АВС и АDС: АС — общая, по условию АВ = DС, АD = ВC, АВС =АDС (по 3 признаку равенства треугольников), 1 = 2, при этом 1 и 2 накрест лежащие при пересечении прямых АD и ВC секущей АС, по признаку параллельности двух прямых АDВС.

3. Итак, АD = ВC, АDВС, по 1 0 признаку параллелограмма, четырехугольник АВСD — параллелограмм. Что и требовалось доказать.

3 0 . Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник параллелограмм.

Доказательство:

Дано: АВСD — четырехугольник, АС и DВ диагонали, АС ∩ DВ = О, АО = ОС, DО = ОВ.

Доказать: АВСD — параллелограмм.

Доказательство:

1. Рассмотрим АОD и ВОС: по условию АО = ОС, DО = ОВ, АОD и ВОС (как вертикальные углы), АОD =ВОС (по 1 признаку равенства треугольников), АD = ВC и 1 = 2.