Точка пересечения высот произвольного треугольника центр окружности описанной около треугольника

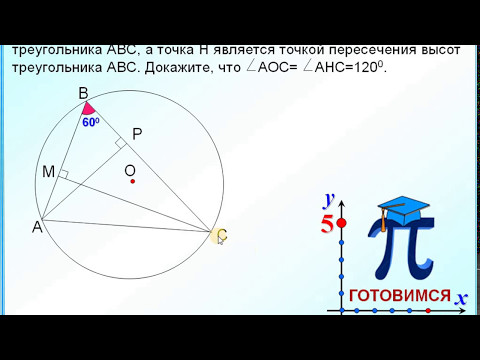
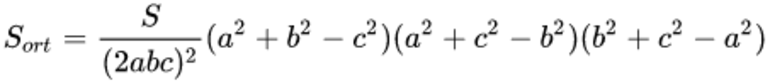Видео:Точка O центр окружности описанной около остроугольного треугольникаСкачать

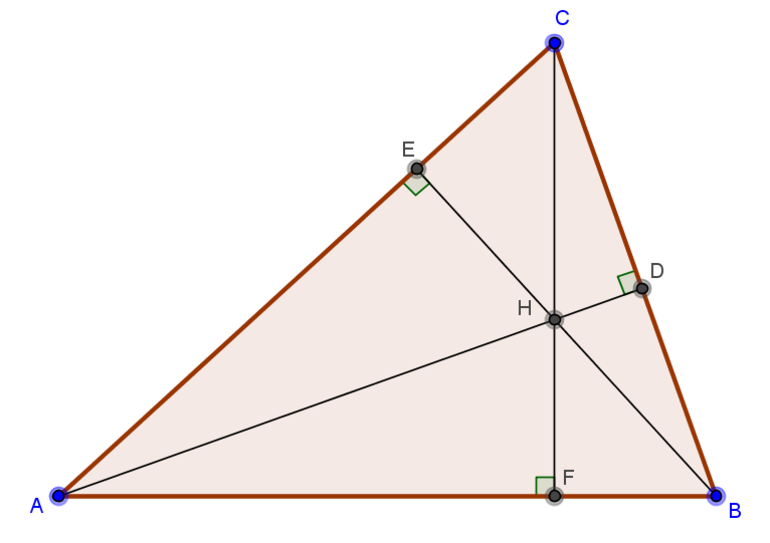
Что такое высота

Если из вершины опустить перпендикуляр на противоположную сторону, получится отрезок, который именуется высотой. В равнобедренном треугольнике 2 отрезка равны, а в равностороннем равны все 3.

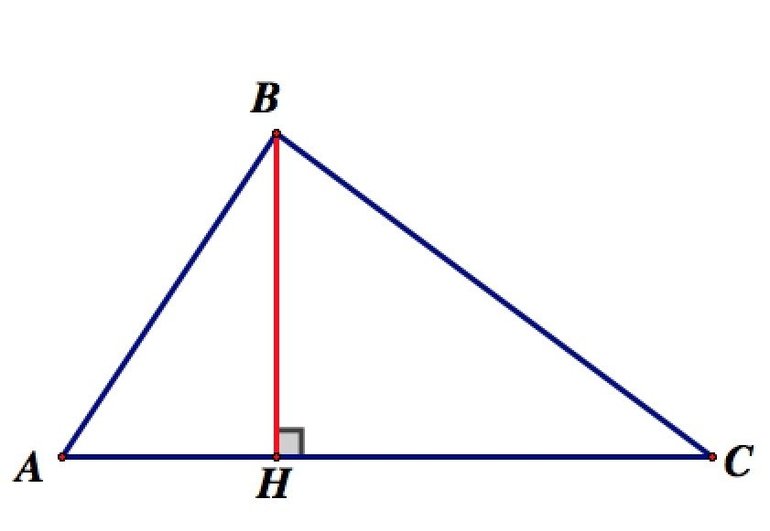
У фигур с углами 90 и более градусов высота попадает на противоположную сторону. В случае острого угла дело обстоит иначе. Прямая попадет только на продолжение противоположной стороны и будет находиться вне самой фигуры. Таким образом, если все углы острые, отрезки будут находиться внутри, как и ортоцентр. В тупоугольной фигуре два из трех отрезков будут проходить за его пределами — ортоцентр окажется вне фигуры.

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Свойства ортоцентра

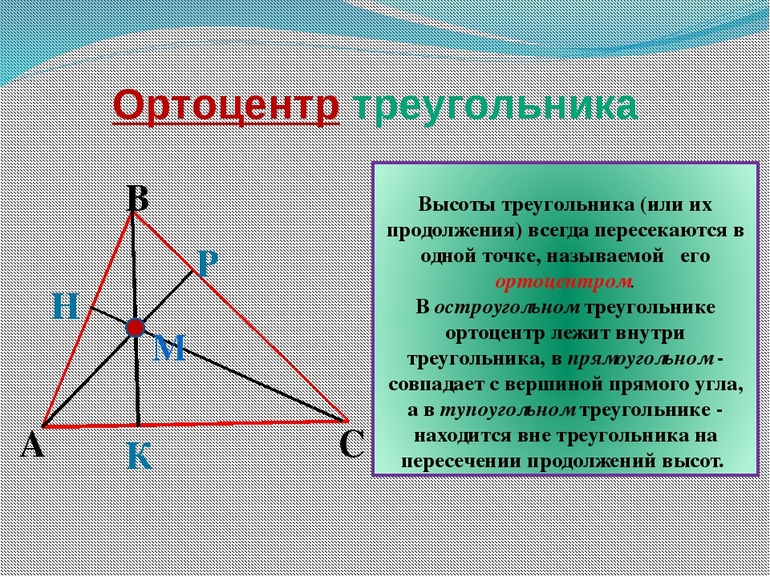
Свойства высот треугольника, пересекающихся в одной точке, давно изучены и описаны. Согласно основному из них, все 3 высоты всегда пересекаются в одном месте. Иногда, чтобы найти это место, отрезки нужно продлить, превратив в ортогональные прямые.

Ортоцентр по отношению к фигуре может быть расположен:

• внутри;
• снаружи;
• в вершине (у прямоугольных треугольников)

Ортоцентр — важная в геометрии характеристика, влияющая на нахождение золотого сечения.

Так называется маленький треугольник, расположенный внутри основного, находящийся на пересечении его трех параметров:

Золотое сечение может представлять собой не только треугольную фигуру, но и отрезок. В правильном треугольнике медианы, биссектрисы и высоты совпадают, значит, золотое сечение превращается в точку.

Полезные факты

Местонахождение ортоцентра имеет некоторые закономерности. Их знание принесет пользу при решении задач.

Пусть:

• H — ортоцентр в ABC;
• О — центр описанной окружности.

Тогда:

• окружности, описанные вокруг АБС, АНВ, CHB, HCA, равны:
• отрезок BH вдвое длиннее отрезка АС;
• середины отрезков AC и BH разделены расстоянием, равным радиусу описанной окружности.

Задача Фаньяно

Это классическая теорема. Она возникла в процессе поиска фигур с наименьшим периметром. Теорему доказал Фаньяно — итальянский математик и инженер. Это произошло еще в начале XVIII века.

Формулировка: ортотреугольник, то есть фигура, полученная соединением трех оснований треугольника, проведенный внутри остроугольного треугольника, имеет самый маленький периметр изо всех возможных, вписанных в данную фигуру.

Площадь ортотреугольника рассчитывается по формуле:

Здесь S — площадь, а, b, c — стороны.

Существует понятие ортоцентрической системы. Оно включает в себя 3 вершины и место пересечения их высот. Любая из данных четырех точек будет являться ортоцентром треугольника, образованного тремя остальными.

Видео:Центр окружности описанной вокруг треугольникаСкачать

История изучения

Важное значение имеет место пересечения медиан или центр тяжести. Вместе с ортоцентром это еще одна «замечательная точка», которая была известна еще древним грекам. Так их стали называть начиная с 18 века, другое название «особенные».

Исследование этих точек стало началом для создания геометрии треугольника, основателем которой считается Леонард Эйлер. Ученый показал, что в любом треугольнике точки соединения высот, медиан и центр описанного круга находятся на одной линии, которую позже назвали прямой Эйлера.

В позапрошлом веке была обнаружена окружность 9 точек или Фейербаха. Она состоит из оснований медиан, высот и центров высот. Оказалось, что все эти точки лежат на общей окружности, центр которой находится на линии Эйлера.

Каждый отрезок, прочерченный из ортоцентра до соединения с описанной окружностью, всегда будет делиться линией Эйлера на 2 равные части.

Треугольник — удивительная фигура, изучением которой занимается целый раздел геометрии. Ортоцентр и его свойства имеют широкое применение в практической жизни, например, в строительстве. Этот показатель настолько важен и распространен, что существуют калькуляторы, позволяющие определить местонахождение точки по координатам вершин.

Видео:Построить описанную окружность (Задача 1)Скачать

Свойства высот треугольника. Ортоцентр

Схема 1. В треугольнике АВС проведены высоты АМ и СК.
Н – точка пересечения высот треугольника (ортоцентр), Н=АМ∩СК

Запомните этот рисунок. Перед вами – схема, из которой можно получить сразу несколько полезных фактов.

1. Треугольники МВК и △АВС, подобны, причем коэффициент подобия
, если , и , если

1. Четырехугольник АКМС можно вписать в окружность. Эта вспомогательная окружность поможет решить множество задач.
2. Четырехугольник ВКМН также можно вписать в окружность.
3. Радиусы окружностей, описанных вокруг треугольников АВС, АНС, ВНС и АВН, равны.
4. ,где R – радиус описанной окружности .

Докажем эти факты по порядку.

1) Заметим, что на рисунке есть подобные треугольники. Это АВМ и СВК, прямоугольные треугольники с общим углом В, и они подобны по двум углам

Мы получили, что в треугольниках МВК и АВС стороны, прилежащие к углу В, пропорциональны. Получаем, что по углу и двум сторонам.

2) Докажем, что вокруг четырехугольника АКМС можно описать окружность. Для этого необходимо и достаточно, чтобы суммы противоположных углов четырехугольника АКМС были равны .

Пусть ∠ACB=∠BKM=γ (поскольку треугольники МВК и АВС подобны), тогда
– как смежный с углом ВКМ. Получили, что , и это значит, что четырехугольник AKMC можно вписать в окружность.

3) Рассмотрим четырехугольник KBMH. Его противоположные углы ВКН и ВМН — прямые, их сумма равна , и значит, четырехугольник КВМН можно вписать в окружность.

4) По теореме синусов, радиус окружности, описанной вокруг треугольника АВС,

Радиус окружности, описанной вокруг треугольника АНС,
Мы помним, что . Значит, синусы углов АВС и АНС равны, и радиусы окружностей, описанных вокруг треугольников АВС и АНС равны.

5) Докажем, что ,где R – радиус описанной окружности . Поскольку четырехугольник КВМН можно вписать в окружность и углы ВКН и ВМН – прямые, отрезок ВН является диаметром этой окружности. Треугольник МВК также вписан в эту окружность, и по теореме синусов, .

Диаметр окружности, описанной вокруг треугольника АВС, равен Поскольку треугольники МВК и АВС подобны, отношение диаметров описанных вокруг них окружностей равно . Получили, что

Задача ЕГЭ по теме «Высоты треугольника» (Профильный уровень, №16)

2. В остроугольном треугольнике KMN проведены высоты KB и NA.

а) Докажите, что угол ABK равен углу ANK.

б) Найдите радиус окружности, описанной около треугольника ABM, если известно, что и

а) Докажем, что
(по двум углам). Запишем отношение сходственных сторон:
Но это значит, что (по углу и двум сторонам), причем .

— смежный с углом ,
,
,четырехугольник ABNK можно вписать в окружность.
(опираются на одну дугу).

Видео:Задание 16 ЕГЭ по математикеСкачать

Входная контрольная работа 9 класс

Просмотр содержимого документа
«Входная контрольная работа 9 класс»

Тестовая контрольная работа по геометрии составлена в форме ГИА. Контрольная работа состоит из двух частей. 1 часть – 7 заданий, 2 часть – 2 задания.

Задания 1 части оцениваются в 1 балл, задания 2 части – 2 балла.

Задания, оцениваемые одним баллом, считаются выполненными верно, если указан верный ответ.

Задания, оцениваемые двумя баллами, считаются выполненными верно, если учащийся выбрал правильный путь решения, из письменной записи решения понятен ход его рассуждений, получен верный ответ. В этом случае ему выставляется 2 балла. Если в решении допущена ошибка, не носящая принципиального характера и не влияющая на общую правильность хода решения, то учащемуся засчитывается 1 балл.

Контрольная работа рассчитана на 45 минут.

При составлении контрольной работы использовались задания открытого банка заданий по математике. ( http://mathgia.ru/or/gia12/Main.html )

Входная контрольная работа по геометрии

Площадь прямоугольника АВСD равна 15. Найдите сторону ВС прямоугольника, если известно, что АВ = 3.

Найдите медиану прямоугольного треугольника, проведенную к гипотенузе, равной 14.

Два острых угла прямоугольного треугольника относятся как 4:5. Найдите больший острый угол треугольника. Ответ дайте в градусах.

В ромбе АВСD проведена диагональ АС. Найдите ÐАВС, если известно, что

В 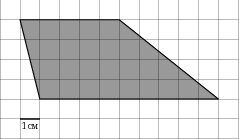прямоугольном треугольнике АВК гипотенуза АВ равна 13, катет АК равен 12, катет ВК равен 8. Найдите тангенс угла А.

На клетчатой бумаге с клетками размером 1 см х 1 см изображена фигура (см. рисунок). Найдите ее площадь в квадратных сантиметрах

Укажите в ответе номера верных утверждений в порядке возрастания:

в прямоугольном треугольнике высота может совпадать с одной из его сторон.

точка пересечения высот произвольного треугольника – центр окружности, описанной около этого треугольника.

высота может лежать и вне треугольника.

треугольник со сторонами 6,8,10 — прямоугольный.

существует треугольник со сторонами 6, 8, 15.

Человек ростом 1,7 м стоит на расстоянии 12 шагов от столба, на котором висит фонарь. Тень человека равна двум шагам. На какой высоте (в метрах) расположен фонарь?

Пря­мая ка­са­ет­ся окруж­но­сти в точке K. Точка O — центр окруж­но­сти. Хорда KM об­ра­зу­ет с ка­са­тель­ной угол, рав­ный 83°. Най­ди­те ве­ли­чи­ну угла OMK. Ответ дайте в гра­ду­сах.

Входная контрольная работа по геометрии

Площадь параллелограмма АВСD равна 35. Найдите сторону ВС параллелограмма, если известно, что высота, проведенная к этой стороне, равна 7.

Найдите гипотенузу прямоугольного треугольника, если медиана, проведенная к этой гипотенузе, равна 4.

Один из двух острых угла прямоугольного треугольника на 20 о больше другого. Найдите больший острый угол. Ответ дайте в градусах.

В ромбе АВСD проведена диагональ АС. Найдите ÐАВС, если известно,

В 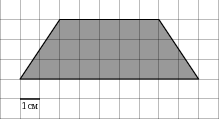прямоугольном треугольнике АВК гипотенуза АВ равна 16, катет АК равен 12, катет ВК равен 8. Найдите синус угла А.

На клетчатой бумаге с клетками размером 1 см х 1 см изображена фигура (см. рисунок). Найдите ее площадь в квадратных сантиметрах

Укажите в ответе номера верных утверждений в порядке возрастания:

в равностороннем треугольнике все высоты равны.

точка пересечения медиан произвольного треугольника – это центр окружности, описанной около этого треугольника.

медиана – это отрезок, соединяющий середины двух сторон треугольника.

треугольник со сторонами 6,8,9 — не существует.

треугольник со сторонами 3, 4, 5 — прямоугольный.

Найдите длину солнечной тени от здания высотой 16 м, если солнечная тень от человека ростом 1 м 80 см равна 2 м 70 см.

Ка­са­тель­ные в точ­ках A и B к окруж­но­сти с цен­тром O пе­ре­се­ка­ют­ся под углом 72°. Най­ди­те угол ABO. Ответ дайте в гра­ду­сах.

Входная контрольная работа по геометрии

Площадь прямоугольника АВСD равна 45. Найдите сторону ВС прямоугольника, если известно, что АВ = 9.

Найдите гипотенузу прямоугольного треугольника, если радиус описанной окружности равен 11.

Один из острых углов прямоугольного треугольника на 24 0 больше другого. Найдите больший острый угол. Ответ дайте в градусах.

В ромбе АВСD проведена диагональ АС. Найдите ÐАВС, если известно, что ÐАСD = 10°.

В 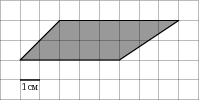прямоугольном треугольнике АВК гипотенуза АВ равна 13, катет АК равен 12, катет ВК равен 8. Найдите косинус угла А.

На клетчатой бумаге с клетками размером 1 см х1 см изображена фигура (см. рисунок). Найдите ее площадь в квадратных сантиметрах

Укажите в ответе номера верных утверждений в порядке возрастания:

точка пересечения биссектрис является центром вписанной окружности любого треугольника.

отношение периметров подобных многоугольников равно квадрату коэффициента подобия.

в прямоугольнике диагонали перпендикулярны.

в равнобокой трапеции диагонали равны

треугольник со сторонами 5, 12, 13 – прямоугольный.

Человек ростом 1,6 м стоит на расстоянии 10 шагов от столба, на котором висит фонарь. Тень человека равна пяти шагам. На какой высоте (в метрах) расположен фонарь?

Из точки А про­ве­де­ны две ка­са­тель­ные к окруж­но­сти с цен­тром в точке О. Най­ди­те ра­ди­ус окруж­но­сти, если угол между ка­са­тель­ны­ми равен 60°, а рас­сто­я­ние от точки А до точки О равно 8.

Входная контрольная работа по геометрии

Площадь параллелограмма АВСD равна 45. Найдите сторону ВС параллелограмма, если известно, что высота, проведенная к этой стороне, равна 5.

Найдите медиану прямоугольного треугольника, проведенную к гипотенузе, если гипотенуза равна 14.

Два острых угла прямоугольного треугольника относятся как 1:9. Найдите больший острый угол. Ответ дайте в градусах.

В ромбе АВСD проведена диагональ АС. Найдите ÐАВС, если известно, что ÐАСD = 20°.

В 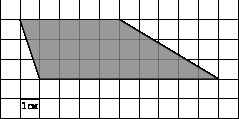прямоугольном треугольнике АВК гипотенуза АВ равна 17, катет АК равен 15, катет ВК равен 8. Найдите тангенс угла А.

На клетчатой бумаге с клетками размером 1 см х 1 см изображена фигура (см. рисунок). Найдите ее площадь в квадратных сантиметрах

Укажите в ответе номера верных утверждений в порядке возрастания:

у прямоугольника диагонали равны.

медиана всегда делит пополам один из углов треугольника.

радиус описанной около прямоугольного треугольника окружности равен одной из его медиан.

отношение площадей подобных треугольников равно квадрату коэффициента подобия.

треугольник со сторонами 3, 4, 6 – не существует.

Длина солнечной тени от дерева равна 24 м. Вертикальный шест высотой 1 м 50 см в тот же момент отбрасывает тень длиной 1 м 60 см. Вычислите высоту дерева.

На от­рез­ке AB вы­бра­на точка C так, что AC = 75 и BC = 10. По­стро­е­на окруж­ность с цен­тром A, про­хо­дя­щая через C. Най­ди­те длину от­рез­ка ка­са­тель­ной, про­ведённой из точки B к этой окруж­но­сти.

🎥 Видео

Точка пересечения высот | ЕГЭ-2018. Задание 16. Математика. Профильный уровень | Борис ТрушинСкачать

2038 центр окружности описанной около треугольника ABC лежит на стороне ABСкачать

ОГЭ 2019. Задание 17. Разбор задач. Геометрия. Окружность.Скачать

Свойство окружности, описанной около равнобедренного треугольникаСкачать

Точка пересечения высот треугольника.Скачать

Центром окружности, описанной около треугольника ... | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать

Геометрия Радиус окружности описанной около треугольника ABC равен 6 см Найдите радиус окружностиСкачать

Через центр О окружности, описанной около остроугольного треугольника ДВИ МГУСкачать

ОГЭ 2021 Задание 24Скачать

2031 окружность центром в точке О описана около равнобедренного треугольника ABCСкачать

Досрочный ЕГЭ 2020. Задание №16Скачать

#30. Регион ВсОШ 2023, 10.5Скачать

Диагностическая работа-1 в формате ОГЭ. Задача-25Скачать

✓ Расстояние от вершины треугольника до точки пересечения высот | Ботай со мной #113 | Борис ТрушинСкачать

Задание 25 Вписанный треугольникСкачать