Нахождение сторон в равностороннем треугольнике (2 видео)

Стороны равностороннего треугольника

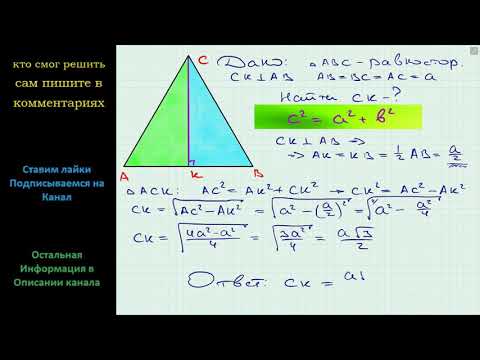
Треугольник, у которого все три стороны равны, называется равносторонним. Периметр такого треугольника равен стороне (а) умноженной на 3 (количество сторон): : P = 3a.
Кроме сторон, у такого треугольника одинаковы и все углы, по 60 градусов каждый, т.к. сумма всех углов треугольника равна 180 градусам. Перпендикуляр, опущенный из вершины треугольника на его противоположную сторону, является его высотой. Она делит треугольник на 2 одинаковых прямоугольных треугольника, у которых гипотенузой будет сторона равностороннего треугольника (а), одним из катетов — высота (h), а другим катетом — половина его основания или (а/2), т.к в треугольнике все стороны равны.
По теореме Пифагора в прямоугольном треугольнике квадрат гипотенузы (в нашем случае она является и стороной равностороннего треугольника) равен сумме квадрата высоты h и квадрата половины основания (половины стороны а):

a 2 = h 2 + a 2 /2 2 ,

где а — сторона, h — высота равностороннего треугольника.
После проведенных преобразований, выводим формулу для расчета стороны равностороннего треугольника по его высоте:

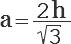
Т.е. сторона равностороннего треугольника (а) равна удвоенной высоте (2h) на корень квадратный из трех.

Содержание

Все формулы для треугольника
1. Как найти неизвестную сторону треугольника
2. Как узнать сторону прямоугольного треугольника
3. Формулы сторон равнобедренного треугольника
4. Найти длину высоты треугольника
Свойства равностороннего треугольника: теория и пример задачи
Определение равностороннего треугольника
Свойства равностороннего треугольника
Свойство 1
Свойство 2
Свойство 3
Свойство 4
Свойство 5
Свойство 6
Пример задачи
🎦 Видео

Видео:НАЙДИТЕ ВЫСОТУ РАВНОСТОРОННЕГО ТРЕУГОЛЬНИКАСкачать

Все формулы для треугольника

Видео:Задание 15 ОГЭ. Медиана равностороннего треугольникаСкачать

1. Как найти неизвестную сторону треугольника

Вычислить длину стороны треугольника: по стороне и двум углам или по двум сторонам и углу.

a , b , c — стороны произвольного треугольника

α , β , γ — противоположные углы

Формула длины через две стороны и угол (по теореме косинусов), ( a ):

* Внимательно , при подстановке в формулу, для тупого угла ( α >90), cos α принимает отрицательное значение

Формула длины через сторону и два угла (по теореме синусов), ( a):

Видео:Известна биссектриса равностороннего треугольника. Найти сторону этого треугольника. ОГЭ №16Скачать

2. Как узнать сторону прямоугольного треугольника

Есть следующие формулы для определения катета или гипотенузы

a , b — катеты

c — гипотенуза

α , β — острые углы

Формулы для катета, ( a ):

Формулы для катета, ( b ):

Формулы для гипотенузы, ( c ):

Формулы сторон по теореме Пифагора, ( a , b ):

Видео:Геометрия Равносторонний треугольникСкачать

3. Формулы сторон равнобедренного треугольника

Вычислить длину неизвестной стороны через любые стороны и углы

b — сторона (основание)

a — равные стороны

α — углы при основании

β — угол образованный равными сторонами

Формулы длины стороны (основания), (b ):

Формулы длины равных сторон , (a):

Видео:ОГЭ 16🔴Скачать

4. Найти длину высоты треугольника

Высота— перпендикуляр выходящий из любой вершины треугольника, к противоположной стороне (или ее продолжению, для треугольника с тупым углом).

Высоты треугольника пересекаются в одной точке, которая называется — ортоцентр.

H — высота треугольника

a — сторона, основание

b, c — стороны

β , γ — углы при основании

p — полупериметр, p=(a+b+c)/2

R — радиус описанной окружности

S — площадь треугольника

Формула длины высоты через стороны, ( H ):

Формула длины высоты через сторону и угол, ( H ):

Формула длины высоты через сторону и площадь, ( H ):

Формула длины высоты через стороны и радиус, ( H ):

Видео:Высота равностороннего треугольника равна 13√3 ... | ОГЭ 2017 | ЗАДАНИЕ 9 | ШКОЛА ПИФАГОРАСкачать

Свойства равностороннего треугольника: теория и пример задачи

В данной статье мы рассмотрим определение и свойства равностороннего (правильного) треугольника. Также разберем пример решения задачи для закрепления теоретического материала.

Видео:Площадь равностороннего треугольникаСкачать

Определение равностороннего треугольника

Равносторонним (или правильным) называется треугольник, в котором все стороны имеют одинаковую длину. Т.е. AB = BC = AC.

Примечание: правильный многоугольник – это выпуклый многоугольник, имеющий равные стороны и углы между ними.

Видео:№488. Найдите: а) высоту равностороннего треугольника, если его сторона равна 6 см;Скачать

Свойства равностороннего треугольника

Свойство 1

В равностороннем треугольнике все углы равны 60°. Т.е. α = β = γ = 60°.

Свойство 2

В равностороннем треугольнике высота, проведенная к любой из сторон, одновременно является биссектрисой угла, из которого она проведена, а также медианой и серединным перпендикуляром.

CD – медиана, высота и серединный перпендикуляр к стороне AB, а также биссектриса угла ACB.

Свойство 3

В равностороннем треугольнике биссектрисы, медианы, высоты и серединные перпендикуляры, проведенные ко всем сторонам, пересекаются в одной точке.

Свойство 4

Центры вписанной и описанной вокруг равностороннего треугольника окружностей совпадают и находятся на пересечении медиан, высот, биссектрис и серединных перпендикуляров.