Определение и свойство смежных углов определение параллельных прямых

Определение 1. Смежными называются два угла, у которых одна сторона общая, а другие стороны являются продолжениями друг друга.

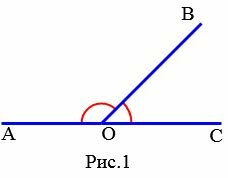На Рис.1 углы AOB и BOC смежные, так как сторона OB общая для этих углов, а стороны OA и OC являются продолжениями друг друга. Поскольку угол AOC является развернутым углом, то сумма смежных углов равна 180°:

.

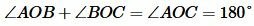(1)

Видео:Смежные углы. 7 класс.Скачать

Свойства смежных углов

1. Сумма смежных углов равна 180°

2. Если оба смежных угла равны между собой, то они являются прямыми.

3. В паре смежных углов всегда один острый, а другой тупой, или оба угла прямые.

4. Синусы смежных углов равны.

5. Косинусы, тангенсы и котангенсы смежгых углов равны, но имеют противоположный знак.

Справедливость пунктов 2 и 3 очевидны и следуют из (1).

Доказательство пункта 4. Обозначим через α один из смежных углов. Тогда величина другого угла будет равна 180°−α. Но (см. статью Формулы приведения тригонометрических функций онлайн)

.

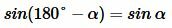То есть синусы смежных углов равны.

Доказательство пункта 5. Обозначим через α один из смежных углов. Тогда величина другого угла будет равна 180°−α. Но

,

,

.

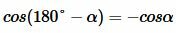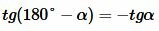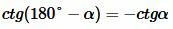То есть косинусы, тангенсы и котангенсы смежных углов равны, но имеют противоположный знак.

Видео:7 класс, 11 урок, Смежные и вертикальные углыСкачать

Геометрия. Урок 2. Углы

Смотрите бесплатные видео-уроки на канале Ёжику Понятно.

Видео-уроки на канале Ёжику Понятно. Подпишись!

Содержание страницы:

• Углы

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Понятие угла

Угол – геометрическая фигура, образованная двумя лучами, выходящими из одной точки.

Стороны угла – лучи, которые образуют угол.

Вершина угла – точка, из которой выходят лучи.

Угол называют тремя заглавными латинскими буквами, которыми обозначены вершина и две точки, расположенные на сторонах угла.

Важно: в названии буква, обозначающая вершину угла, стоит между двумя буквами, обозначающими точки на сторонах угла. Так, угол, изображенный на рисунке, можно назвать: ∠ A O B или ∠ B O A , но ни в коем случае не ∠ O A B , ∠ O B A , ∠ A B O , ∠ B A O .

Величину угла измеряют в градусах. ∠ A O B = 24 ° .

Видео:7 класс, 25 урок, Признаки параллельности двух прямыхСкачать

Виды углов:

Видео:Геометрия 7 класс (Урок№19 - Признаки параллельности прямых.)Скачать

Биссектриса угла

Биссектриса угла – это луч с началом в вершине угла, делящий его на два равных угла.

Биссектриса угла – это геометрическое место точек, равноудаленных от сторон угла.

O D – биссектриса угла ∠ A O B . Она делит этот угол на два равных угла.

∠ A O D = ∠ B O D = ∠ A O B 2

Точка D – произвольная точка на биссектрисе. Она равноудалена от сторон O A и O B угла ∠ A O B .

Видео:Геометрия 7 класс (Урок№18 - Параллельные прямые.)Скачать

Углы, образованные при пересечении двух прямых

Вертикальные углы – пара углов, у которых стороны одного угла являются продолжением сторон второго.

Свойство: вертикальные углы равны.

Смежные углы – пара углов, у которых одна сторона общая, а две другие стороны расположены на одной прямой.

Свойство: сумма смежных углов равна 180 ° .

( 1 ) и ( 3 )
( 2 ) и ( 4 )

называются вертикальными .

По свойству вертикальных углов:

∠ C O D = ∠ A O B
∠ B O D = ∠ A O C

( 1 ) и ( 2 )
( 2 ) и ( 3 )
( 3 ) и ( 4 )
( 4 ) и ( 1 )

называются смежными .

По свойству смежных углов:

∠ C O D + ∠ D O B = 180 ° ∠ D O B + ∠ B O A = 180 ° ∠ B O A + ∠ A O C = 180 ° ∠ A O C + ∠ C O D = 180 °

Видео:Геометрия 7 класс (Урок№21 - Свойства параллельных прямых.)Скачать

Углы, образованные при пересечении двух прямых секущей

Прямая, пересекающая две заданные прямые, называется секущей этих прямых.

Существует пять видов углов, которые образуются при пересечении двух прямых секущей.

( 1 ) и ( 5 )
( 2 ) и ( 6 )
( 3 ) и ( 7 )
( 4 ) и ( 8 )

называются соответственными .
(Легко запомнить: они соответствуют друг другу, похожи друг на друга).

( 3 ) и ( 5 )
( 4 ) и ( 6 )

называются внутренними односторонними .
(Легко запомнить: лежат по одну сторону от секущей, между двумя прямыми).

( 1 ) и ( 7 )
( 2 ) и ( 8 )

называются внешними односторонними .
(Легко запомнить: лежат по одну сторону от секущей по разные стороны от двух прямых).

( 3 ) и ( 6 )
( 4 ) и ( 5 )

называются внутренними накрест лежащими .
(Легко запомнить: лежат между двумя прямыми, расположены наискосок друг относительно друга).

( 1 ) и ( 8 )
( 2 ) и ( 7 )

называются внешними накрест лежащими .
(Легко запомнить: лежат по разные стороны от двух прямых, расположены наискосок друг относительно друга).

Если прямые, которые пересекает секущая, параллельны , то углы имеют следующие свойства:

• Соответственные углы равны.
• Внутренние накрест лежащие углы равны.
• Внешние накрест лежащие углы равны.
• Сумма внутренних односторонних углов равна 180 ° .
• Сумма внешних односторонних углов равна 180 ° .

Видео:SOS-ГЕОМЕТРИЯ! Отрезки и углы, смежные и вертикальные углы | Математика TutorOnlineСкачать

Сумма углов многоугольника

Сумма углов произвольного n -угольника вычисляется по формуле:

S n = 180 ° ⋅ ( n − 2 )

где n – это количество углов в n -угольнике.

Пользуясь этой формулой, можно вычислить сумму углов для произвольного n -угольника.

Сумма углов треугольника: S 3 = 180 ° ⋅ ( 3 − 2 ) = 180 °

Сумма углов четырехугольника: S 4 = 180 ° ⋅ ( 4 − 2 ) = 360 °

Сумма углов пятиугольника: S 5 = 180 ° ⋅ ( 5 − 2 ) = 540 °

Так можно продолжать до бесконечности.

Правильный многоугольник – это выпуклый многоугольник, у которого все стороны равны и все углы равны.

На рисунках изображены примеры правильных многоугольников:

Чтобы найти величину угла правильного n -угольника , необходимо сумму углов этого многоугольника разделить на количество углов.

α n = 180 ° ⋅ ( n − 2 ) n

Видео:Геометрия 7 класс | Вертикальные, смежные, накрест лежащие и другие углы (теория) | МАТЕМАТИКА 2021Скачать

Примеры решений заданий из ОГЭ

Модуль геометрия: задания, связанные с углами

Видео:СВОЙСТВА ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ. §15 геометрия 7 классСкачать

Признаки и свойства параллельных прямых

Видео:Параллельные прямые — Признак Параллельности Прямых и Свойства УгловСкачать

Признаки параллельных прямых

1. Если две прямые параллельны третьей прямой, то они являются параллельными:

2. Если две прямые перпендикулярны третьей прямой, то они параллельны:

Остальные признаки параллельности прямых основаны на углах, образующихся при пересечении двух прямых третьей.

3. Если сумма внутренних односторонних углов равна 180°, то прямые параллельны:

Если ∠1 + ∠2 = 180°, то a || b.

4. Если соответственные углы равны, то прямые параллельны:

5. Если внутренние накрест лежащие углы равны, то прямые параллельны:

Видео:Смежные и вертикальные углы. Практическая часть - решение задачи. 7 класс.Скачать

Свойства параллельных прямых

Утверждения, обратные признакам параллельности прямых, являются их свойствами. Они основаны на свойствах углов, образованных пересечением двух параллельных прямых третьей прямой.

1. При пересечении двух параллельных прямых третьей прямой, сумма образованных ими внутренних односторонних углов равна 180°:

Если a || b, то ∠1 + ∠2 = 180°.

2. При пересечении двух параллельных прямых третьей прямой, образованные ими соответственные углы равны:

3. При пересечении двух параллельных прямых третьей прямой, образованные ими накрест лежащие углы равны:

Следующее свойство является частным случаем для каждого предыдущего:

4. Если прямая на плоскости перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой:

Пятое свойство — это аксиома параллельности прямых:

5. Через точку, не лежащую на данной прямой, можно провести только одну прямую, параллельную данной прямой:

📽️ Видео

7 класс, 24 урок, Определение параллельных прямыхСкачать

7 класс, 28 урок, Аксиома параллельных прямыхСкачать

Определение параллельных прямых | Геометрия 7-9 класс #25 | ИнфоурокСкачать

Свойства параллельных прямых - 7 класс геометрияСкачать

Геометрия 7 класс (Урок№6 - Смежные и вертикальные углы. Аксиомы и теоремы.)Скачать

Пары углов в геометрииСкачать

7 класс - Геометрия - Определение параллельных прямых. Признаки параллельности прямыхСкачать

Свойство смежных угловСкачать