Можно ли провести через точку не лежащую на прямой параллельную этой прямой

Укажите номера верных утверждений.

1) Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.

2) Треугольник со сторонами 1, 2, 4 существует.

3) Если в ромбе один из углов равен 90°, то такой ромб — квадрат.

4) Центр описанной около треугольника окружности всегда лежит внутри этого треугольника.

Если утверждений несколько, запишите их номера в порядке возрастания.

Проверим каждое из утверждений.

1) «Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой» — верно, это аксиома планиметрии.

2) «Треугольник со сторонами 1, 2, 4 существует» — неверно: для того, чтобы существовал треугольник, сумма любых его двух сторон должна быть больше третьей стороны.

3) «Если в ромбе один из углов равен 90°, то такой ромб — квадрат.» — верно, в этом случае противоположный угол тоже будет равен 90°, а значит и два других (равных) угла будут равны по 90°.

4) «Центр описанной около треугольника окружности всегда лежит внутри этого треугольника.» — неверно, центр описанной вокруг прямоугольного треугольника окружности, лежит на его стороне.

Аналоги к заданию № 93: 171 197 311684 357582 Все

Видео:Через точку, не лежащую на данной прямой, можно ... | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать

Аксиома параллельных прямых

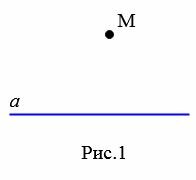
Рассмотрим прямую a и точку M, не лежащую на этой прямой (Рис.1). Докажем, что через точку M можно провести прямую, параллельную прямой a.

Проведем через точку M прямую c, перпендикулярно прямой a, и прямую b, перпендикулярно прямой c (Рис.2).

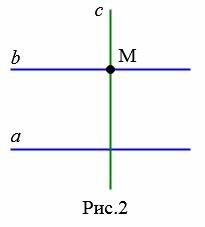Поскольку a и b перпендикулярны прямой с, то они параллельны (статья Перпендикулярные прямые Теорема 1 и статья Параллельные прямые. Признаки параллельности прямых Определение 1). Таким образом через точку M проходит прямая, параллельная прямой a.

Возникает вопрос, существует ли другая прямая, проходящая через точку M параллельно прямой a. Интуитивно ясно, что если немного повернуть прямую b вокруг оси M, то прямые b и a пересекутся. Но доказать это утверждение до сих пор не удалось. основываясь на стальных аксиомах геометрии.

Таким образом имеем это утверждение в виде аксиомы:

Аксиома 1. Через точку, не лежащую на данной прямой проходит только одна прямая, параллельная данной.

Следствие 1. Если прямая пересекает одну из параллельных прямых, то она пересекает и другую.

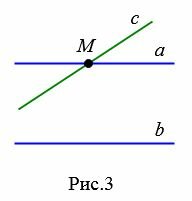Доказательство. Пусть заданы параллельные прямые a и b и пусть прямая c пересекает a в точке M (Рис.3). Докажем, что прямая c пересекает и прямую b.

Предположим обратное, т.е. c не пересекает b. Тогда получается, что через точку M проходят две прямые a и c параллельно прямой b, что невозможно (Аксиома 1). Следовательно прямая с пересекает и прямую b.

Следствие 2. Если две прямые параллельны третьей прямой, то они параллельны.

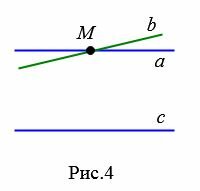Действительно. Предположим, что прямые a и b параллельны прямой c. Докажем, что прямая a параллельна прямой b. Предположим обратное, т.е. прямые a и b пересекаются в точке M (Рис.4). Тогда получается, что через точку M проходят две прямые, параллельные прямой c. Но это невозможно (Аксиома 1). Значит прямые a и b параллельны.

Видео:Геометрия 10 класс (Урок№4 - Параллельность прямых, прямой и плоскости.)Скачать

Стереометрия. Страница 2

Видео:№11. Даны прямая и точка, не лежащая на этой прямой. Докажите, что все прямые, проходящие черезСкачать

1. Параллельность прямых в пространстве

Теорема. Через точку, не лежащую на данной прямой, можно провести только одну прямую, параллельную данной.

Доказательство. Пусть b данная прямая и точка А, не лежащая на данной прямой. Проведем через точку А и прямую b плоскость α. А через точку А прямую a, параллельную прямой b. (Рис.1)

Допустим, что существует другая прямая а’, параллельная прямой b и проходящая через точку А. Тогда через них можно провести плоскость β. Отсюда следует, что через точку А и прямую b можно провести две плоскости. А это невозможно согласно теореме о единственности существования плоскости, проведеной через прямую и не лежащую на ней точку. Таким образом, плоскости α и β совпадают. А следовательно, согласно аксиоме, прямые а и a’ совпадают также.

5. Пример 1

Докажите, что если прямые АВ и CD скрещивающиеся, то прямые АС и BD тоже скрещиваются.

Доказательство:

Пусть даны две скрещивающиеся прямые АВ и CD. Проведем через прямую АВ и точку С плоскость α (Рис.5). Так как прямые АВ и CD скрещивающиеся, то прямая CD не лежит в плоскости α, а пересекает ее в одной точке С.

Отсюда следует, что точка D не принадлежит плоскости α. Она лежит вне ее.

Таким образом, если мы проведем прямую АС, то она полностью будет принадлежать плоскости α, так как две ее точки А и С принадлежат плоскости α.

А прямая BD не будет принадлежать плоскости α, так как точка D не принадлежит плоскости α. Прямая BD будет пересекать плоскость α в одной точке В.

Отсюда можно сделать вывод, что прямая АС не может пересекать прямую BD, так как прямая АС полностью принадлежит плоскости α. А прямая BD имеет только одну общую точку с плоскостью α, точку В. Но так как точка В не лежит на прямой АС, следовательно, прямые АС и BD не пересекаются. Они являются скрещивающимися.

Рис.5 Задача. Докажите, что если прямые АВ и CD скрещивающиеся.

Пример 2

Точки А, В, С, D не лежат в одной плоскости. Докажите, что прямая, проходящая через середины отрезков АВ и ВС, параллельна прямой, проходящей через середины отрезков AD и CD.

Доказательство:

Пусть даны четыре точки А, В, С, D, которые не лежат в одной плоскости. Проведем плоскость α через точки A, D, C и плосксоть α’ через точки А, В, С (Рис.6). Точки P, S, F, E являются серединами отрезков AB, BC, AD и CD соответственно. Необходимо доказать, что прямая PS параллельна прямой FE.

Рассмотрим треугольник АВС. Он полностью лежит в плоскости α’, так как три его вершины лежат в данной плоскости по построению. Отрезок PS представляет собой среднюю линию треугольника, которая параллельна АС.

Теперь рассмотрим треугольник АСD. Он полностью лежит в плоскости α, так как три его вершины лежат в данной плоскости по построению. Отрезок FE представляет собой среднюю линию треугольника, которая также параллельна АС.

Отсюда можно сделать вывод: если две прямые PS и FE параллельны третьей прямой АС, то они параллельны и между собой. И равны половине основанию АС. Таким образом, PSEF представляет собой параллелограмм.

Рис.6 Задача. Точки А, В, С, D не лежат в одной плоскости.

Пример 3

Даны четыре точки А, В, С, D, не лежащие в одной плоскости. Докажите, что прямые, соединяющие середины отрезков АВ и ВС, АС и BD, AD и BC пересекаются в одной точке.

Доказательство:

Пусть даны четыре точки А, В, С, D, которые не лежат в одной плоскости. Проведем отрезки EP, VS, FT, которые соединят середины сторон AB и CD, BC и AD, AC и BD соответственно (Рис.7).

Из предыдущей задачи нам известно, что четырехугольник EVPS, вершины которого являются серединами отрезков АВ, ВС, СD и AD, есть параллелограмм, у которого EP и VS диагонали. Эти диагонали пересекаются в точке О и делятся этой точкой пополам.

Теперь рассмотрим четырехугольник VTSF. Данный четырехугольник также является параллелограммом, так как его вершины — это середины отрезков BC, BD, AC и AD. А его диагонали VS и FT пересекаются в точке О и делятся этой точкой пополам.

Так как у отрезка VS середина одна, т.е. точка О, то все три диагонали EP, VS и FT пересекаются в этой точке.

Рис.7 Задача. Даны четыре точки А, В, С, D, не лежащие в одной плоскости.

Пример 4

Докажите, что если две плоскости, пересекающиеся по прямой а, пересекают плоскость α по параллельным прямым, то прямая а параллельна плоскости α.

Доказательство:

Пусть даны две плоскости β и γ, пересекающиеся по прямой а (Рис.8). Эти плоскости пересекают плоскость α по параллельным прямым b и с. Необходимо доказать, что прямая а параллельна плоскости α.

Прямая b — это множество точек, которые одновременно принадлежат плоскостям α и γ. Прямая с — это множество точек, которые одновременно принадлежат плоскостям α и β. Так как прямые b и с параллельны, то на этих прямых нет ни одной точки, которая одновременно принадлежала бы трем плоскостям.

Прямая а — это множество точек, которые принадлежат двум плоскостям β и γ. Допустим, что она пересекает плоскость α. Тогда на ней должна быть точка, которая принадлежала бы одновременно трем плоскостям. А следовательно, она одновременно лежала бы на прямых b и с. Но это противоречит условию задачи, так как прямые b и с не пересекаются. Следовательно, прямая а параллельна прямым b и с. А отсюда следует, что она параллельна плоскости α.

Рис.8 Задача. Докажите, что если две плоскости, пересекающиеся по прямой а.

Пример 5

Докажите, что если четыре прямые, проходящие через точку О, пересекают плоскость α в вершинах параллелограмма, то они пересекают любую плоскость, параллельную α и не проходящую через точку О, тоже в вершинах параллелограмма.

Доказательство:

Пусть даны четыре прямые, проходящие через точку О, ОА, ОВ, ОС и OD (Рис.9). Они пересекают плоскость α в точках А, В, С и D соответственно. Проведем плоскость α’, параллельную плоскости α. Тогда прямые ОА, ОВ, ОС и OD пересекут плоскость α’ в точках A’B’C’D’.

Проведем плоскость β через точки А, В, A’, B’. Тогда прямые АВ и A’B’ не пересекаются, так как это прямые пересечения двух параллельных плоскостей α и α’ с секущей плоскостью β.

Отсюда следует, что прямые ВС и В’С’, CD и C’D’, AD и A’D’ параллельны. А так как АВ параллельна CD, а ВС параллельна AD, то следовательно, А’В’ параллельна C’D’, а В’С’ параллельна A’D’.

Таким образом, A’B’C’D’ также является параллелограммом.

Рис.9 Задача. Докажите, что если четыре прямые, проходящие через точку А.

📺 Видео

Построение прямой, параллельной даннойСкачать

Через точку, не лежащую на данной прямой, можно ... | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать

Построить перпендикуляр к прямой из точки не принадлежащей этой прямой.Скачать

Как построить прямую, перпендикулярную данной прямой через точку, которая лежит на данной прямойСкачать

№35. Через точку М, не лежащую на прямой а, проведены две прямые, не имеющие общих точек с прямой а.Скачать

Перпендикуляр к прямой через заданную точку.Скачать

6 и 7 кл.Провести через точки не лежащие на прямой а.,прямые параллельные данной прямойСкачать

Построение перпендикуляра к прямойСкачать

7 класс, 16 урок, Перпендикуляр к прямойСкачать

Геометрия. 7 класс. Теоремы. Т4. Перпендикуляр к прямой.Скачать

10 класс, 4 урок, Параллельные прямые в пространствеСкачать

Параллельность прямых. 10 класс.Скачать

Построение прямой, параллельной даннойСкачать

Параллельные прямые | Математика | TutorOnlineСкачать

Главная > Учебные материалы > Математика: Стереометрия. Страница 2 1.Параллельность прямых в пространстве. 2.Признак параллельности прямых. 3.Признак параллельности плоскостей. 4.Свойства параллельных плоскостей. 5.Примеры.

1 2 3 4 5 6 7 8

Рис. 1 Параллельность прямых в пространстве. Видео:Параллельность прямой и плоскости. 10 класс.Скачать 2.Признак параллельности прямых Теорема. Две прямые, параллельные третьей прямой, параллельны. Доказательство. Пусть прямые а и b лежат в разных плоскостях и параллельны прямой с. Доказать, что прямые а и b параллельны между собой. (Рис.2) Проведем через прямую a и c плоскость α. Через прямые b и c плоскость β. Прямая с — прямая пересечения плоскостей α и β. Отметим на прямой а точку А. Проведем через точку А и прямую b плоскость γ. Тогда плоскость γ будет пересекать плоскость α по прямой а’. Прямая a’ либо паралельна прямой c, либо ее пересекает. Допустим прямая а’ пересекает прямую с. Тогда эта точка пересечения принадлежит плоскости β, т.к. прямая с принадлежит двум плоскостям α и β. А т.к. прямая а’ полностью принадлежит плоскости γ, а прямая b есть прямая пересечения плоскостей γ и β, то это означает, что она пересекает и прямую b. А это означает, что прямые b и c пересекаются, т.к. прямая a’ пересекает плоскость β только в одной точке, которая должна принадлежать двум прямым b и с. А это противоречит условию. Следовательно прямая a’ не пересекает прямую с. Она ей параллельна. Согласно аксиоме, на плоскости α, через точку, не лежащую на данной прямой, можно провести только одну прямую, параллельную данной. И эта прямая а. Т.е. прямые а и а’ совпадают. Это значит, что прямые а и b параллельны. Рис.2 Признак параллельности прямых Видео:Параллельные прямые циркулемСкачать 3. Признак параллельности плоскостей Теорема: если две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны. Доказательство. Пусть α и β данные плоскости. Прямая а параллельна прямой а 1 . Прямая b параллельна b 1 (Рис.3). Допустим, что плоскости α и β пересекаются по прямой с. Тогда прямая с должна пересекать, как минимум, одну из прямых на каждой плоскости. Пусть это будут прямые а и а 1 . Т.к. прямые а и а 1 параллельны, следовательно они пересекают прямую с в разных точках Е и Е 1 . Проведем через две параллельные прямые а и а 1 плоскость γ. Тогда точки Е и Е 1 , которые лежат на прямой с, будут принадлежать плоскости γ. Следовательно, прямая с полностью принадлежит плоскости γ. Отсюда следует, что: а ∈ α, γ. а 1 ∈ β, γ. с ∈ α, β,γ т.е. плоскости α и γ пересекаются по двум прямым а и с, а плоскости β и γ пересекаются по прямым а 1 и с. Рис. 3 Признак параллельности плоскостей. Согласно аксиоме стереометрии, это невозможно, т.к. две плоскости могут пересекаться только по одной прямой. И следовательно, наше предположение неверно. Плоскости α и β не пересекаются, они параллельны. Видео:№197. Через точку, не лежащую на прямой р, проведены четыре прямые. Сколько из этих прямыхСкачать 4. Свойства параллельных плоскостей Теорема: Если две параллельные плоскости пересекаются третьей, то прямые пересечения параллельны. Доказательство. Пусть даны две параллельные плоскости α и β (Рис.4). Плоскость γ пересекает их по прямым а и b. Допустим, что прямые пересечения плоскостей пересекаются. Это прямые а и b’. Прямая а — это множество точек, принадлежащих плоскостям α и γ. А так как прямая b’ представляет собой множество точек, пренадлежащих двум плоскостям β и γ, то отсюда следует, что существует точка пересечения прямых а и b’, которая принадлежит плоскости α. И следовательно, плоскости α и β имеют общую точку. А это противоречит условию, т.к. плоскости α и β не пересекаются, они параллельны. Следовательно, прямые а и b лежат в одной плоскости и не пересекаются. Т.е. они тоже параллельны. Рис. 4 Свойства параллельных плоскостей.