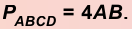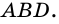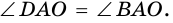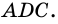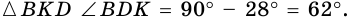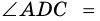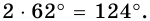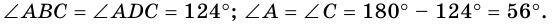Если в четырехугольнике диагонали взаимно перпендикулярны то он ромб

ОБРАТНАЯ ТЕОРЕМА для данной теоремы (или к данной теореме) — теорема. в которой условием является заключение, а заключением — условие данной теоремы. Данная теорема по отношению к обратной теореме называется прямой (исходной). В то же время обратная теорема к обратной теореме будет данной теоремой; поэтому прямая и обратная теоремы называются взаимно обратными. Если прямая (данная) теорема верна, то обратная теорема не всегда верна. Например, если четырехугольник — ромб, то его диагонали взаимно перпендикулярны (прямая теорема). Если в четырехугольнике диагонали взаимно перпендикулярны, то четырехугольник есть ромб — это неверно, т. е. обратная теорема неверна. Взаимно обратные теоремы тесно связаны с необходимым и достаточным условиями (признаками).

Видео:Все про РОМБ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // Геометрия 8 классСкачать

Если в четырехугольнике диагонали взаимно перпендикулярны то он ромб

Какие из данных утверждений верны? Запишите их номера.

1) Если две стороны одного треугольника соответственно равны двум сторонам другого треугольника, то такие треугольники равны.

2) Площадь круга меньше квадрата длины его диаметра.

3) Если в четырёхугольнике диагонали перпендикулярны, то этот четырёхугольник — ромб.

Проверим каждое из утверждений.

1) «Если две стороны одного треугольника соответственно равны двум сторонам другого треугольника, то такие треугольники равны» — неверно; верным будет утверждение: «Если две стороны одного треугольника и угол между ними соответственно равны двум сторонам и углу другого треугольника, то такие треугольники равны».

2) «Площадь круга меньше квадрата длины его диаметра» — верно, поскольку площадь круга равна , а .

3) «Если в четырёхугольнике диагонали перпендикулярны, то этот четырёхугольник — ромб» — неверно; верным являлось бы утверждение «Если в параллелограмме диагонали перпендикулярны, то такой параллелограмм — ромб», но не любой четырёхугольник — параллелограмм.

Видео:Геометрия Признак ромба Если диагонали параллелограмма перпендикулярны, то этот параллелограмм ромбСкачать

Ромб и его свойства, определение и примеры с решением

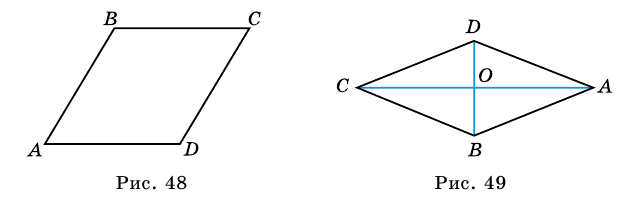
Ромбом называют параллелограмм, у которого все стороны равны (рис. 48).

Так как ромб является параллелограммом, то он имеет все свойства параллелограмма.

1. Сумма любых двух соседних углов ромба равна 180°.

2. У ромба противолежащие углы равны.

3. Диагонали ромба точкой пересечения делятся пополам.

4. Периметр ромба

Кроме того, ромб имеет еще и такое свойство.

5. Диагонали ромба взаимно перпендикулярны и делят его углы пополам.

Доказательство:

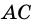
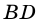
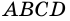
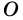
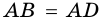
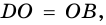
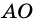
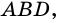
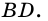
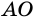
Пусть и — диагонали ромба (рис. 49), — точка их пересечения. Поскольку и то — медиана равнобедренного треугольника проведенная к основанию Поэтому является также высотой и биссектрисой треугольника

Следовательно, 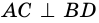и

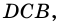
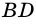
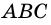
Аналогично можно доказать, что диагональ АС делит пополам угол а диагональ делит пополам углы и

Пример:

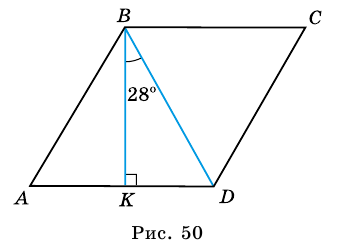
Угол между высотой и диагональю ромба проведенными из одной вершины, равен 28°. Найдите углы ромба.

Решение:

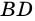
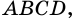
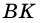
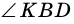
Пусть — диагональ ромба а — его высота (рис. 50), = 28°.

1) В

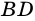
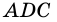
2) Так как делит угол пополам, то

3) Тогда

Ответ. 124°, 56°, 124°, 56°.

Рассмотрим признаки ромба.

Теорема (признаки ромба). Если в параллелограмме: 1) две соседние стороны равны, или 2) диагонали пересекаются под прямым углом, или 3) диагональ делит пополам углы параллелограмма, — то параллелограмм является ромбом.

Доказательство:

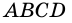
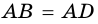
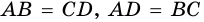
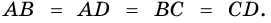
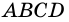
1) Пусть — параллелограмм (рис. 48). Так как (по условию) и (по свойству параллелограмма), то Следовательно, — ромб.

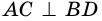
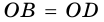
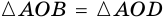
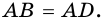
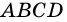
2) Пусть (рис. 49). Поскольку (по свойству параллелограмма), то (по двум катетам). Следовательно, По п. 1 этой теоремы — ромб.

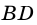
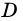
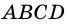
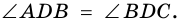
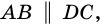
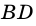
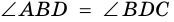
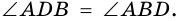
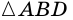
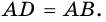
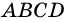
3) Диагональ делит пополам угол параллелограмма (рис. 49), то есть Так как — секущая, то (как внутренние накрест лежащие). Следовательно, Поэтому по признаку равнобедренного треугольника — равнобедренный и По п. 1 этой теоремы — ромб.

Пример:

Докажите, что если в четырехугольнике все стороны равны, то этот четырехугольник — ромб.

Доказательство:

Пусть 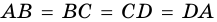(рис. 48).

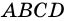
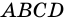
1) Так как противолежащие стороны четырехугольника попарно равны, то — параллелограмм по признаку параллелограмма.

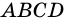
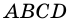
2) У параллелограмма соседние стороны равны. Поэтому — ромб (по признаку ромба).

Слово «ромб» греческого происхождения, которое в древние времена означало вращающееся тело, веретено, волчок. Ромб тогда связывали с сечением веретена, на которое намотаны нити.

В «Началах» Евклида термин «ромб» встречается единожды, а свойства ромба Евклид вообще не рассматривал.

• Квадрат и его свойства
• Трапеция и ее свойства
• Площадь трапеции
• Центральные и вписанные углы
• Четырехугольники и окружность
• Параллелограмм, его свойства и признаки
• Площадь параллелограмма
• Прямоугольник и его свойства

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

🎦 Видео

Если в четырёхугольнике диагонали перпендикулярны ... | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать

№408. Докажите, что параллелограмм является ромбом, если: а) его диагонали взаимноСкачать

Геометрия Доказательство Диагонали ромба перпендикулярны и являются биссектрисами его угловСкачать

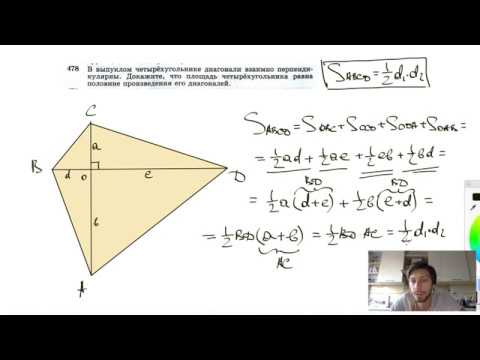
№478. В выпуклом четырехугольнике диагонали взаимно перпендикулярны. Докажите, что площадьСкачать

Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

Если диагонали параллелограмма перпендикулярны, то это ... | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать

№410. Является ли четырехугольник квадратом, если его диагонали: а) равны и взаимноСкачать

Геометрия Признак ромба Если диагональ параллелограмма является биссектрисой его угла, то этотСкачать

№521. Докажите, что если диагонали четырехугольника ABCD взаимно перпендикулярны, то AD2 +ВС2 =AB2+CСкачать

8 класс, 8 урок, Ромб и квадратСкачать

Если диагонали выпуклого четырёхугольника равны ... | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать

Геометрия 8. Урок 4 - Прямоугольник, ромб, квадрат - свойства и признаки.Скачать

РОМБ . §5 геометрия 8 классСкачать

Ромб. 8 класс.Скачать

Все про ПАРАЛЛЕЛОГРАММ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // ГеометрияСкачать

Геометрия Доказать, что если в четырехугольнике диагонали лежат на биссектрисах его углов, то такойСкачать

ПЕРВАЯ ЗАДАЧА 2024 ГОДА!!!Скачать

Ромб, признаки. 8 класс.Скачать