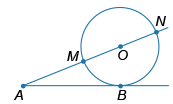
К окружности проведена касательная ab и секущая пересекающая

К окружности с центром O проведены касательная AB и секущая AO. Секущая AO пересекает окружность в точках M и N (см. рис.). Найдите длину AB (в см), если AM и AN равны 9 см и 25 см соответственно.

По теореме о касательной и секущей AB 2 =AM•AN=9•25=225

AB 2 =AM•AN=9•25=225

Ответ: 15
2 1 8 0 8 4 7

Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

К окружности проведена касательная AB и секущая пересекающая окружность в точках C и D?

Геометрия | 5 — 9 классы

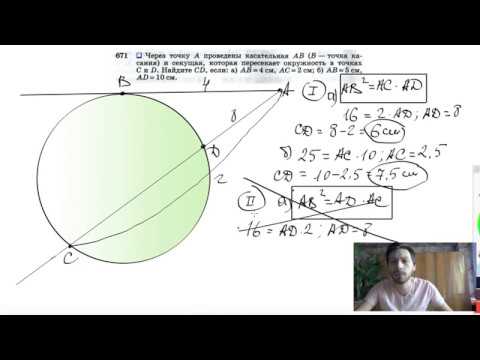
К окружности проведена касательная AB и секущая пересекающая окружность в точках C и D.

Известно, что AC = 4 CD = 5.

АД = АС + СД = 4 + 5 = 9, АВ в квадрате = АС * СД = 4 * 9 = 36, АВ = 6.

Видео:Секущая и касательная. 9 класс.Скачать

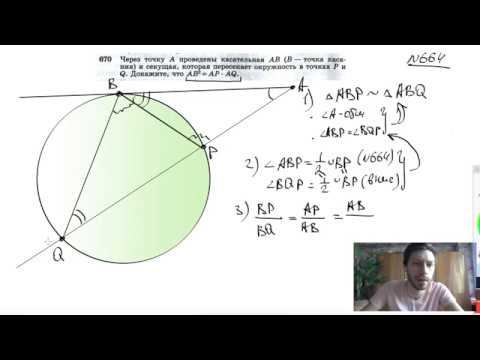
Через точку А к окружности проведены касательная АВ (точка В лежит на окружности) и секущая, которая пересекает окружность в точках Е и F и проходит через центр окружности?

Через точку А к окружности проведены касательная АВ (точка В лежит на окружности) и секущая, которая пересекает окружность в точках Е и F и проходит через центр окружности.

Найти радиус окружности, если АВ = 12 , а АF = 18.

Видео:№671. Через точку А проведены касательная АВ (В — точка касания) и секущая, которая пересекаетСкачать

Из точки Е к окружности проведены касательная АЕ и секущая ВЕ?

Из точки Е к окружности проведены касательная АЕ и секущая ВЕ.

Эта секущая пересекает окружность в точках В и С.

Найдите длину АЕ, если ВС 5 см, ВЕ 4 см.

Видео:ОГЭ за одну минуту | ОГЭ, математика, задание 16 (окружность и касательная)Скачать

Из точки E к окружности проведены касательная AE и секущая BE?

Из точки E к окружности проведены касательная AE и секущая BE.

Эта секущая пересекает окружность в точках B и C.

Найдите длину AE, если BC = 5 см, BE = 4 см.

Видео:Окружность, касательная, секущая и хорда | МатематикаСкачать

К окружности проведены касательная и секущая из одной точки m?

К окружности проведены касательная и секущая из одной точки m.

Касательная касается окружности в точке N, секущая пересекает окружность в точках P и Q.

Известно что MP = 4, PQ = 5 Найдите MN.

Видео:№670. Через точку А проведены касательные АВ (В — точка касания) и секущая, которая пересекаетСкачать

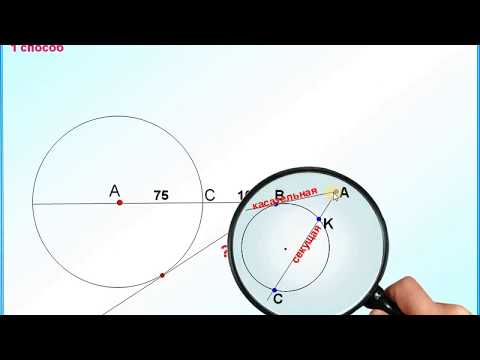
Из точки М к окружности, радиус которой равен 4 см, проведены касательная, касающаяся окружности в точке С, и секущая, проходящая через центр О окружности и пересекающая ее в точках А и В так, что МА ?

Из точки М к окружности, радиус которой равен 4 см, проведены касательная, касающаяся окружности в точке С, и секущая, проходящая через центр О окружности и пересекающая ее в точках А и В так, что МА = АО.

Точка N — середина дуги АС окружности, заключенной между секущей и касательной.

Найдите площадь треугольника МON.

Видео:Пойми Этот Урок Геометрии и получай 5-ки — Касательная и ОкружностьСкачать

Из точки Е к окружности проведены касательная АЕ и секущая ВЕ?

Из точки Е к окружности проведены касательная АЕ и секущая ВЕ.

Эта секущая пересекает окружность в точках В и С.

Найдите длину АЕ, еслм ВС = 5 см, ВЕ = 4 см.

Видео:Геометрия Докажите, что если через точку A к окружности проведены касательная AM (M – точка касания)Скачать

Из одной точки проведены к окружности касательная и секущая?

Из одной точки проведены к окружности касательная и секущая.

Найти касательную, если известно, что она меньше внутреннего отрезка секущей на 4 и больше внешнего отрезка на 4.

Видео:Теорема о секущей и касательной, о секущих, о пересекающихся хордах | Теоремы об окружностях - 1Скачать

ПОМОГИТЕ?

Через конец В диаметра АВ проведена секущая, которая пересекается в точке D с касательной, проведённой через другой конец диаметра А ; радиус окружности равен 3 см.

Найдите длину отрезка касательной AD, если известно, что секущая BD в точке пересечения с окружностью делится пополам.

Видео:Касательная и секущая к окружности.Скачать

Очень нужна ваша помощь?

Очень нужна ваша помощь!

Из точки А вне окружности проведены касательная АВ и секущая АД, пересекающая окружность в точке С.

Видео:Геометрия Через точку A проведены к окружности касательная AM (M – точка касания) и секущаяСкачать

ИЗ ТОЧКИ А К ОКРУЖНОСТИ ПРОВЕДЕНЫ КАСАТЕЛЬНАЯ АВ И СЕКУЩАЯ АС?

ИЗ ТОЧКИ А К ОКРУЖНОСТИ ПРОВЕДЕНЫ КАСАТЕЛЬНАЯ АВ И СЕКУЩАЯ АС.

Перед вами страница с вопросом К окружности проведена касательная AB и секущая пересекающая окружность в точках C и D?, который относится к категории Геометрия. Уровень сложности соответствует учебной программе для учащихся 5 — 9 классов. Здесь вы найдете не только правильный ответ, но и сможете ознакомиться с вариантами пользователей, а также обсудить тему и выбрать подходящую версию. Если среди найденных ответов не окажется варианта, полностью раскрывающего тему, воспользуйтесь «умным поиском», который откроет все похожие ответы, или создайте собственный вопрос, нажав кнопку в верхней части страницы.

Видео:8 класс, 32 урок, Касательная к окружностиСкачать

Касательная к окружности

О чем эта статья:

Видео:#59. Олимпиадная задача о касательной к окружности!Скачать

Касательная к окружности, секущая и хорда — в чем разница

В самом названии касательной отражается суть понятия — это прямая, которая не пересекает окружность, а лишь касается ее в одной точке. Взглянув на рисунок окружности ниже, несложно догадаться, что точку касания от центра отделяет расстояние, в точности равное радиусу.

Касательная к окружности — это прямая, имеющая с ней всего одну общую точку.

Если мы проведем прямую поближе к центру окружности — так, чтобы расстояние до него было меньше радиуса — неизбежно получится две точки пересечения. Такая прямая называется секущей, а отрезок, расположенный между точками пересечения, будет хордой (на рисунке ниже это ВС ).

Секущая к окружности — это прямая, которая пересекает ее в двух местах, т. е. имеет с ней две общие точки. Часть секущей, расположенная внутри окружности, будет называться хордой.

Видео:Секретная теорема из учебника геометрииСкачать

Свойства касательной к окружности

Выделяют четыре свойства касательной, которые необходимо знать для решения задач. Два из них достаточно просты и легко доказуемы, а вот еще над двумя придется немного подумать. Рассмотрим все по порядку.

Касательная к окружности и радиус, проведенный в точку касания, взаимно перпендикулярны.

Не будем принимать это на веру, попробуем доказать. Итак, у нас даны:

• окружность с центральной точкой А;
• прямая а — касательная к ней;
• радиус АВ, проведенный к касательной.

Докажем, что касательная и радиус АВ взаимно перпендикулярны, т.е. а ⟂ АВ.

Пойдем от противного — предположим, что между прямой а и радиусом АВ нет прямого угла и проведем настоящий перпендикуляр к касательной, назвав его АС.

В таком случае наш радиус АВ будет считаться наклонной, а наклонная, как известно, всегда длиннее перпендикуляра. Получается, что АВ > АС. Но если бы это было на самом деле так, наша прямая а пересекалась бы с окружностью два раза, ведь расстояние от центра А до нее — меньше радиуса. Но по условию задачи а — это касательная, а значит, она может иметь лишь одну точку касания.

Итак, мы получили противоречие. Делаем вывод, что настоящим перпендикуляром к прямой а будет вовсе не АС, а АВ.

Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.

Задача

У нас есть окружность, центр которой обозначен О. Из точки С проведена прямая, и она касается этой окружности в точке А. Известно, что ∠АСО = 28°. Найдите величину дуги АВ.

Мы знаем, что касательная АС ⟂ АО, следовательно ∠САО = 90°.

Поскольку нам известны величины двух углов треугольника ОАС, не составит труда найти величину и третьего угла.

∠АОС = 180° — ∠САО — ∠АСО = 180° — 90° — 28° = 62°

Поскольку вершина угла АОС лежит в центре окружности, можно вспомнить свойство центрального угла — как известно, он равен дуге, на которую опирается. Следовательно, АВ = 62°.

Если провести две касательных к окружности из одной точки, лежащей вне этой окружности, то их отрезки от этой начальной точки до точки касания будут равны.

Докажем и это свойство на примере. Итак, у нас есть окружность с центром А, давайте проведем к ней две касательные из точки D. Обозначим эти прямые как ВD и CD . А теперь выясним, на самом ли деле BD = CD.

Для начала дополним наш рисунок, проведем еще одну прямую из точки D в центр окружности. Как видите, у нас получилось два треугольника: ABD и ACD . Поскольку мы уже знаем, что касательная и радиус к ней перпендикулярны, углы ABD и ACD должны быть равны 90°.

Итак, у нас есть два прямоугольных треугольника с общей гипотенузой AD. Учитывая, что радиусы окружности всегда равны, мы понимаем, что катеты AB и AC у этих треугольников тоже одинаковой длины. Следовательно, ΔABD = ΔACD (по катету и гипотенузе).. Значит, оставшиеся катеты, а это как раз наши BD и CD (отрезки касательных к окружности), аналогично равны.

Важно: прямая, проложенная из стартовой точки до центра окружности (в нашем примере это AD), делит угол между касательными пополам.

Задача 1

У нас есть окружность с радиусом 4,5 см. К ней из точки D, удаленной от центра на 9 см, провели две прямые, которые касаются окружности в точках B и C. Определите градусную меру угла, под которым пересекаются касательные.

Решение

Для этой задачи вполне подойдет уже рассмотренный выше рисунок окружности с радиусами АВ и АC. Поскольку касательная ВD перпендикулярна радиусу АВ , у нас есть прямоугольный треугольник АВD. Зная длину его катета и гипотенузы, определим величину ∠BDA.

∠BDA = 30° (по свойству прямоугольного треугольника: угол, лежащий напротив катета, равного половине гипотенузы, составляет 30°).

Мы знаем, что прямая, проведенная из точки до центра окружности, делит угол между касательными, проведенными из этой же точки, пополам. Другими словами:

∠BDC = ∠BDA × 2 = 30° × 2 = 60°

Итак, угол между касательными составляет 60°.

Задача 2

К окружности с центром О провели две касательные КМ и КN. Известно, что ∠МКN равен 50°. Требуется определить величину угла ∠NМК.

Решение

Согласно вышеуказанному свойству мы знаем, что КМ = КN. Следовательно, треугольник МNК является равнобедренным.

Углы при его основании будут равны, т.е. ∠МNК = ∠NМК.

∠МNК = (180° — ∠МКN) : 2 = (180° — 50°) : 2 = 65°

Соотношение между касательной и секущей: если они проведены к окружности из одной точки, лежащей вне окружности, то квадрат расстояния до точки касания равен произведению длины всей секущей на ее внешнюю часть.

Данное свойство намного сложнее предыдущих, и его лучше записать в виде уравнения.

Начертим окружность и проведем из точки А за ее пределами касательную и секущую. Точку касания обозначим В, а точки пересечения — С и D. Тогда CD будет хордой, а отрезок AC — внешней частью секущей.

Задача 1

Из точки М к окружности проведены две прямые, пусть одна из них будет касательной МA, а вторая — секущей МB. Известно, что хорда ВС = 12 см, а длина всей секущей МB составляет 16 см. Найдите длину касательной к окружности МA.

Решение

Исходя из соотношения касательной и секущей МА 2 = МВ × МС.

Найдем длину внешней части секущей:

МС = МВ — ВС = 16 — 12 = 4 (см)

МА 2 = МВ × МС = 16 х 4 = 64

Задача 2

Дана окружность с радиусом 6 см. Из некой точки М к ней проведены две прямые — касательная МA и секущая МB . Известно, что прямая МB пересекает центр окружности O. При этом МB в 2 раза длиннее касательной МA . Требуется определить длину отрезка МO.

Решение

Допустим, что МО = у, а радиус окружности обозначим как R.

В таком случае МВ = у + R, а МС = у – R.

Поскольку МВ = 2 МА, значит:

МА = МВ : 2 = (у + R) : 2

Согласно теореме о касательной и секущей, МА 2 = МВ × МС.

(у + R) 2 : 4 = (у + R) × (у — R)

Сократим уравнение на (у + R), так как эта величина не равна нулю, и получим:

Поскольку R = 6, у = 5R : 3 = 30 : 3 = 10 (см).

Ответ: MO = 10 см.

Угол между хордой и касательной, проходящей через конец хорды, равен половине дуги, расположенной между ними.

Это свойство тоже стоит проиллюстрировать на примере: допустим, у нас есть касательная к окружности, точка касания В и проведенная из нее хорда AВ. Отметим на касательной прямой точку C, чтобы получился угол AВC.

Задача 1

Угол АВС между хордой АВ и касательной ВС составляет 32°. Найдите градусную величину дуги между касательной и хордой.

Решение

Согласно свойствам угла между касательной и хордой, ∠АВС = ½ АВ.

АВ = ∠АВС × 2 = 32° × 2 = 64°

Задача 2

У нас есть окружность с центром О, к которой идет прямая, касаясь окружности в точке K. Из этой точки проводим хорду KM, и она образует с касательной угол MKB, равный 84°. Давайте найдем величину угла ОMK.

Решение

Поскольку ∠МКВ равен половине дуги между KM и КВ, следовательно:

КМ = 2 ∠МКВ = 2 х 84° = 168°

Обратите внимание, что ОМ и ОK по сути являются радиусами, а значит, ОМ = ОК. Из этого следует, что треугольник ОMK равнобедренный.

∠ОКМ = ∠ОМК = (180° — ∠КОМ) : 2

Так как центральный угол окружности равен угловой величине дуги, на которую он опирается, то:

∠ОМК = (180° — ∠КОМ) : 2 = (180° — 168°) : 2 = 6°

🎬 Видео

ОГЭ Задание 16 Свойство касательной и секущей. Теорема ПифагораСкачать

касательная и секущая в окружностиСкачать

Задание 25 Свойство касательной и хордыСкачать

ЕГЭ по математике. Задание №16 #11Скачать

Окружность №16 из ОГЭ. Свойства хорд, касательных, секущих.Скачать

Касательная к окружности и её свойстваСкачать