Если диагональ вписанного четырехугольника биссектриса

Вписанные четырехугольники и их свойства

Теорема Птолемея

Вписанные четырёхугольники и их свойства

Определение 1 . Окружностью, описанной около четырёхугольника, называют окружность, проходящую через все вершины четырёхугольника (рис.1). В этом случае четырёхугольник называют четырёхугольником, вписанным в окружность, или вписанным четырёхугольником .

Теорема 1 . Если четырёхугольник вписан в окружность, то суммы величин его противоположных углов равны 180° .

Доказательство . Угол ABC является вписанным углом, опирающимся на дугу ADC (рис.1). Поэтому величина угла ABC равна половине угловой величины дуги ADC . Угол ADC является вписанным углом, опирающимся на дугу ABC . Поэтому величина угла ADC равна половине угловой величины дуги ABC . Отсюда вытекает, что сумма величин углов ABC и ADC равна половине угловой величины дуги, совпадающей со всей окружностью, т.е. равна 180° .

Если рассмотреть углы BCD и BAD , то рассуждение будет аналогичным.

Теорема 1 доказана.

Теорема 2 (Обратная к теореме 1) . Если у четырёхугольника суммы величин его противоположных углов равны 180°, то около этого четырёхугольника можно описать окружность.

Доказательство . Докажем теорему 2 методом «от противного». С этой целью рассмотрим окружность, проходящую через вершины A , B и С четырёхугольника, и предположим, что эта окружность не проходит через вершину D . Приведём это предположение к противоречию. Рассмотрим сначала случай, когда точка D лежит внутри круга (рис.2).

Продолжим отрезок CD за точку D до пересечения с окружностью в точке E , и соединим отрезком точку E с точкой A (рис.2). Поскольку четырёхугольник ABCE вписан в окружность, то в силу теоремы 1 сумма величин углов ABC и AEC равна 180° . При этом сумма величин углов ABC и ADC так же равна 180° по условию теоремы 2. Отсюда вытекает, что угол ADC равен углу AEC . Возникает противоречие, поскольку угол ADC является внешним углом треугольника ADE и, конечно же, его величина больше, чем величина угла AEC , не смежного с ним.

Случай, когда точка D оказывается лежащей вне круга, рассматривается аналогично.

Теорема 2 доказана.

Перечисленные в следующей таблице свойства вписанных четырёхугольников непосредственно вытекают из теорем 1 и 2.

Площадь произвольного вписанного четырёхугольника можно найти по формуле Брахмагупты:

где a, b, c, d – длины сторон четырёхугольника,
а p – полупериметр, т.е.

Фигура	Рисунок	Свойство
Окружность, описанная около параллелограмма		Окружность можно описать около параллелограмма тогда и только тогда, когда параллелограмм является прямоугольником.
Окружность, описанная около ромба		Окружность можно описать около ромба тогда и только тогда, когда ромб является квадратом.
Окружность, описанная около трапеции		Окружность можно описать около трапеции тогда и только тогда, когда трапеция является равнобедренной трапецией.
Окружность, описанная около дельтоида		Окружность можно описать около дельтоида тогда и только тогда, когда дельтоид состоит из двух одинаковых прямоугольных треугольников.
Произвольный вписанный четырёхугольник

Площадь произвольного вписанного четырёхугольника можно найти по формуле Брахмагупты:

где a, b, c, d – длины сторон четырёхугольника,
а p – полупериметр, т.е.

Окружность, описанная около параллелограмма
	Окружность можно описать около параллелограмма тогда и только тогда, когда параллелограмм является прямоугольником.
Окружность, описанная около ромба
	Окружность можно описать около ромба тогда и только тогда, когда ромб является квадратом.
Окружность, описанная около трапеции
	Окружность можно описать около трапеции тогда и только тогда, когда трапеция является равнобедренной трапецией.
Окружность, описанная около дельтоида
	Окружность можно описать около дельтоида тогда и только тогда, когда дельтоид состоит из двух одинаковых прямоугольных треугольников.
Произвольный вписанный четырёхугольник

Окружность, описанная около параллелограмма

Окружность можно описать около параллелограмма тогда и только тогда, когда параллелограмм является прямоугольником.

Окружность, описанная около ромба

Окружность можно описать около ромба тогда и только тогда, когда ромб является квадратом.

Окружность, описанная около трапеции

Окружность можно описать около трапеции тогда и только тогда, когда трапеция является равнобедренной трапецией.

Окружность, описанная около дельтоида

Окружность можно описать около дельтоида тогда и только тогда, когда дельтоид состоит из двух одинаковых прямоугольных треугольников.

Произвольный вписанный четырёхугольник

Площадь произвольного вписанного четырёхугольника можно найти по формуле Брахмагупты:

где a, b, c, d – длины сторон четырёхугольника,
а p – полупериметр, т.е.

Теорема Птолемея

Теорема Птолемея . Произведение диагоналей вписанного четырёхугольника равно сумме произведений противоположных сторон.

Доказательство . Рассмотрим произвольный четырёхугольник ABCD , вписанный в окружность (рис.3).

Докажем, что справедливо равенство:

Для этого выберем на диагонали AC точку E так, чтобы угол ABD был равен углу CBE (рис. 4).

Заметим, что треугольник ABD подобен треугольнику BCE . Действительно, у этих треугольников по два равных угла: угол ABD равен углу CBE (по построению точки E ), угол ADB равен углу ACB (эти углы являются вписанными углами, опирающимися на одну и ту же дугу). Следовательно, справедлива пропорция:

откуда вытекает равенство:

(1)

Заметим, что треугольник ABE подобен треугольнику BCD . Действительно, у этих треугольников по два равных угла: угол ABE равен углу DBC (углы ABD и EBC равны по построению, угол DBE – общий), угол BAC равен углу BDC (эти углы являются вписанными углами, пирающимися на одну и ту же дугу). Следовательно, справедлива пропорция:

math4school.ru

Четырёхугольники

Основные определения и свойства

Четырёхугольником называется фигура, которая состоит из четырёх точек (вершин) и четырёх отрезков (сторон), которые последовательно соединяют вершины. При этом никакие три из данных точек не должны лежать на одной прямой, а соединяющие их отрезки не должны пересекаться.

Четырёхугольник называется выпуклым, если он расположен в одной полуплоскости относительно прямой, которая содержит любую из его сторон.

Сумма углов выпуклого четырёхугольника равна 360°:

Не существует четырёхугольников, у которых все углы острые или все углы тупые.

Каждый угол четырёхугольника всегда меньше суммы трёх остальных углов:

Каждая сторона четырёхугольника всегда меньше суммы трёх остальных сторон:

Площадь произвольного выпуклого четырёхугольника равна:

Диагоналями четырёхугольника называются отрезки, соединяющие его противолежащие вершины.

Диагонали выпуклого четырёхугольника пересекаются, а невыпуклого – нет.

Площадь произвольного выпуклого четырёхугольника:

Если M , N , P , Q – середины сторон выпуклого четырёхугольника ABCD , а R , S – середины его диагоналей, то четырёхугольники MNPQ , MRPS , NSQR являются параллелограммами и называются параллелограммами Вариньона.

Форма и размеры параллелограммов Вариньона связаны с формой и размерами данного четырёхугольника ABCD . Так MNPQ – прямоугольник, если диагонали четырёхугольника ABCD перпендикулярны; MNPQ – ромб, если диагонали четырёхугольника ABCD равны; MNPQ – квадрат, если диагонали четырёхугольника ABCD перпендикулярны и равны;

Отрезки MP , NQ и RS называются первой, второй и третьей средними линиями выпуклого четырёхугольника.

В параллелограмме, и только в нём, середины диагоналей совпадают, и потому третья средняя линия вырождается в точку. Для других четырёхугольников средние линии – отрезки.

Все средние линии четырёхугольника пересекаются в одной точке и делятся ею пополам:

MG=GP , NG=GQ , RG=GS .

Сумма квадратов средних линий четырёхугольника равна четверти суммы квадратов всех его сторон и диагоналей:

MP 2 + NQ 2 + RS 2 = ¼ (AB 2 +BC 2 +CD 2 +AD 2 +AC 2 +BD 2 ).

Если β – угол между первой и второй средними линиями четырёхугольника, то его площадь:

Равными плитками, которые имеют форму произвольного, не обязательно выпуклого, четырёхугольника можно замостить плоскость так, чтобы не было наложений плиток друг на друга и не осталось непокрытых участков плоскости.

Описанные четырёхугольники

Четырёхугольник называется описанным около окружности (описанным), если существует такая окружность, которая касается всех его сторон, тогда сама окружность называется вписанной.

Четырёхугольник является описанным тогда и только тогда, кода суммы его противолежащих сторон равны:

Для сторон описанного четырёхугольника и радиуса вписанной в него окружности верно:

Площадь описанного четырёхугольника:

где r – радиус вписанной окружности, p – полупериметр четырёхугольника.

Площадь описанного четырёхугольника:

Центр вписанной в четырёхугольник окружности является точкой пересечения биссектрис всех четырёх углов этого четырёхугольника.

Точки касания вписанной окружности отсекают равные отрезки от углов четырёхугольника:

AK = AN , BK = BL , CL = CM , DM = DN .

Если O – центр окружности, вписанной в четырёхугольник ABCD, то

∠AOB+∠COD = ∠BOC+∠AOD =180°.

Для описанного четырёхугольника ABCD со сторонами AB = a , BC = b , CD = c и AD = d верны соотношения:

Вписанные четырёхугольники

Четырёхугольник называется вписанным в окружность (вписанным), если существует окружность, проходящая через все его вершины, тогда сама окружность называется описанной около четырёхугольника.

Выпуклый четырёхугольник является описанным тогда и только тогда, когда сумма его противолежащих углов равна 180°:

Центр описанной около четырёхугольника окружности является точкой пересечения всех четырёх серединных перпендикуляров сторон этого четырёхугольника.

Первая теорема Птолемея. Выпуклый четырёхугольник тогда и только тогда является вписанным, когда выполняется равенство:

Вторая теорема Птолемея. Выпуклый четырёхугольник тогда и только тогда является вписанным, когда выполняется равенство:

Радиус окружности, описанной около четырёхугольника:

Площадь вписанного четырёхугольника:

Диагонали выпуклого четырёхугольника разбивают каждый его угол на два угла. Углы, опирающиеся на одну сторону, называются связанными углами.

Выпуклый четырёхугольник является вписанным тогда и только тогда, когда у него есть хотя бы одна пара равных связанных углов.

У вписанного четырёхугольника любые два связанных угла равны.

Если четырёхугольник одновременно является описанным и вписанным, то его площадь:

Для радиусов описанной и вписанной окружностей данного четырёхугольника и расстояния между центрами этих окружностей выполняется соотношение:

Параллелограмм

Параллелограммом называется четырёхугольник, противолежащие стороны которого попарно параллельны:

У параллелограмма противолежащие стороны равны и противолежащие углы равны:

Сумма любых двух соседних углов параллелограмма равна 180°:

∠A +∠ B =∠ B +∠ C =∠ C +∠ D =∠ A +∠ D =180°.

Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам:

Каждая диагональ делит параллелограмм на два равных треугольника:

∠ ABC =∠ CDA ; ∠ ABD =∠ CDB .

Две диагонали параллелограмма делят его на четыре равновеликих треугольника:

Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон:

e 2 +f 2 = a 2 +b 2 +a 2 +b 2 = 2(a 2 +b 2 ).

• Если у четырёхугольника противолежащие стороны попарно равны, то этот четырёхугольник – параллелограмм.
• Если у четырёхугольника две противолежащие стороны равны и параллельны, то этот четырёхугольник – параллелограмм.
• Четырёхугольник, диагонали которого в точке пересечения делятся пополам – параллелограмм.
• Если у четырёхугольника противолежащие углы попарно равны, то этот четырёхугольник – параллелограмм.

Высотой параллелограмма называется перпендикуляр, проведённый из вершины параллелограмма к неприлежащей стороне:

Площадь параллелограмма можно определить:

• через его сторону и высоту, проведённую к ней:

• через две его стороны и угол между ними:

Ромбом называется параллелограмм, у которого все стороны равны:

Диагонали ромба пересекаются под прямым углом и являются биссектрисами его углов:

∠ ABD =∠ CBD =∠ ADB =∠ CDB ; ∠ BAC =∠ DAC =∠ BCA =∠ DCA .

В любой ромб можно вписать окружность с центром в точке пересечения его диагоналей.

Радиус окружности, вписанной в ромб, можно вычислить:

• через диагонали ромба и сторону:

• через отрезки, на которые делит сторону ромба точка касания:

Площадь ромба можно определить:

• через сторону и угол ромба:

• через сторону и радиус вписанной окружности:

Прямоугольник

Прямоугольником называется параллелограмм, у которого все углы прямые:

Диагонали прямоугольника равны и точкой пересечения делятся на четыре равных отрезка:

Площадь прямоугольника можно определить:

• через диагонали и угол между ними:

Около любого прямоугольника можно описать окружность с центром в точке пересечения его диагоналей и радиусом, который равен половине диагонали:

Квадрат

Квадрат – это прямоугольник, у которого все стороны равны:

Диагонали квадрата равны и перпендикулярны.

Сторона и диагональ квадрата связаны соотношениями:

У квадрата центры вписанной и описанной окружностей совпадают и находятся в точке пересечения его диагоналей.

Радиус описанной окружности:

Радиус вписанной окружности:

Трапеция

Трапецией называется четырёхугольник у которого только две противолежащие стороны параллельны:

Параллельные стороны называются основаниями трапеции, непараллельные – боковыми сторонами.

Высота трапеции – перпендикуляр, проведённый из произвольной точки одного основания трапеции к прямой, содержащей другое основание трапеции.

Средней линией (первой средней линией) трапеции называется отрезок, который соединяет середины боковых сторон данной трапеции:

Средняя линия трапеции параллельна её основаниям и равна их полусумме:

При продолжении до пересечения боковых сторон трапеции образуются два подобных треугольника с коэффициентом подобия, равным отношению основ:

Δ AED ∼ Δ BEC , k = AD / BC .

Треугольники, образованные основами и отрезками диагоналей подобны с коэффициентом подобия, равным отношению основ:

Δ AОD ∼ Δ CОВ , k = AD / BC .

Площади треугольников, образованных боковыми сторонами и отрезками диагоналей трапеции, равны:

Отрезок, соединяющий середины оснований (вторая средняя линия) трапеции, проходит через точку пересечения диагоналей, а его продолжение – через точку пересечения продолжений боковых сторон:

Отрезок, соединяющий середины диагоналей (третья средняя линия) трапеции, параллелен основаниям и равен их полуразности:

В трапецию можно вписать окружность, если сумма её основ равна сумме боковых сторон:

Центром вписанной в трапецию окружности является точка пересечения биссектрис внутренних углов трапеции.

В трапецию АВСD с основаниями AD и BC можно вписать окружность тогда и только тогда, когда выполняется хотя бы одно из равенств:

Боковые стороны трапеции видны из центра окружности, вписанной в данную трапецию, под прямым углом:

Радиус вписанной в трапецию окружности можно определить:

• через отрезки, на которые делится боковая сторона точкой касания:

Равнобокой называется трапеция, у которой боковые стороны равны:

У равнобокой трапеции:

• углы при основании равны:

• сумма противолежащих углов равна 180?:

Около трапеции можно описать окружность тогда и только тогда, когда она равнобокая.

Стороны и диагональ равнобокой трапеции связаны соотношением:

Трапеция называется прямоугольной, если одна из её боковых сторон перпендикулярна основаниям.

Площадь трапеции можно определить:

• через полусумму оснований (первую среднюю линию) и высоту:

• через диагонали и угол между ними:

Дельтоид

Дельтоид называется четырёхугольник, который имеет две пары равных соседних сторон.

Дельтоид может быть выпуклым или невыпуклым.

Прямые, содержащие диагонали любого дельтоида пересекаются под прямым углом.

В любом дельтоиде углы между соседними неравными сторонами равны.

Площадь любого дельтоида можно определить:

• через две соседние неравные стороны и угол между ними:

В любой выпуклый дельтоид можно вписать окружность.

Если выпуклый дельтоид не является ромбом, то существует окружность, касающаяся продолжений всех четырёх сторон данного дельтоида.

Для невыпуклого дельтоида можно построить окружность, касающуюся двух сторон большей длины и продолжений двух меньших сторон, а также окружность, касающуюся двух меньших сторон и продолжений двух сторон большей длины.

Вокруг дельтоида можно описать окружность тогда и только тогда, когда его неравные стороны образуют углы по 90°.

Радиус окружности, описанной около дельтоида можно определить через две его неравные стороны:

Ортодиагональные четырёхугольники

Четырёхугольник называется ортодиагональным, если его диагонали пересекаются под прямым углом.

Четырёхугольник является ортодиагональным тогда и только тогда, когда выполняется одно из условий:

• для сторон четырёхугольника верно: a²+c² = b²+d ²;
• для площади четырёхугольника верно: S = ½ef ;
• параллелограмм Вариньона с вершинами в серединах сторон четырёхугольника является прямоугольником.

Сумма квадратов противолежащих сторон вписанного в окружность ортодиагонального четырёхугольника равна квадрату диаметра описанной окружности:

Ортодиагональный четырёхугольник является описанным около окружности тогда и только тогда, когда произведения его противолежащих сторон равны:

Если ABCD – ортодиагональный четырёхугольник, описанный около окружности с центром в точке О , то верны соотношения:

Если диагональ вписанного четырехугольника биссектриса

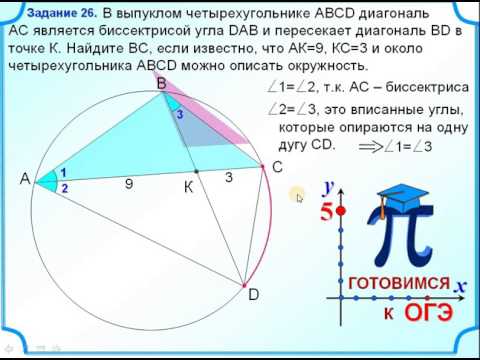
В выпуклом четырехугольнике ABCD диагональ AC является биссектрисой угла BAD и пересекается с диагональю BD в точке E. Известно, что около четырехугольника ABCD можно описать окружность.

б) Найдите AE, если известно, что BC = 7, CE = 4.

а) Углы BCA и BDA равны как вписанные углы, углы BAC и CAD равны по условию, следовательно, треугольники BAC и EAD подобны по двум углам. Значит,

что и требовалось доказать.

б) Пусть AE = x. Углы DBC и DAC равны как вписанные углы, тогда треугольники ABC и BEC подобны по двум углам, откуда

Ответ:

📽️ Видео