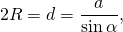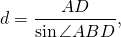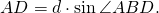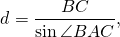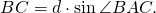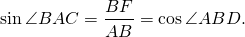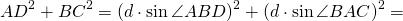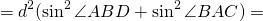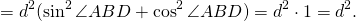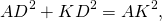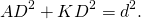В работе представлены основные теоремы и свойства о вписанном четырехугольнике с перпендикулярными диагоналями(с доказательствами)
- Просмотр содержимого документа «Проектно-исследовательская работа по теме: Вписанный четырехугольник с перпендикулярными диагоналями.»
- Если диагонали вписанного четырехугольника перпендикулярны
- Четырехугольники, вписанные в окружность. Теорема Птолемея
- Вписанные четырёхугольники и их свойства
- Теорема Птолемея
- 📸 Видео
Просмотр содержимого документа
«Проектно-исследовательская работа по теме: Вписанный четырехугольник с перпендикулярными диагоналями.»
Вписанный четырехугольник с перпендикулярными диагоналями.
Выполнила учащиеся 8 класса :
Проверила учитель математики:
Четырехугольник с перпендикулярными диагоналями.
Диагонали четырехугольника перпендикулярны тогда и только тогда,когда равны суммы квадратов его противолежащих сторон.
Пусть точка Р — точка пересечения диагоналей четырехугольника.
Введем обозначения длин сторон(рис 1а)








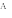
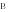
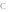
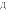

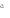

Следовательно,a 2 +c 2 =b 2 +d 2 .
2)Признак.Пусть диагонали четырехугольника
Проведем перпендикулярны BK и DM
к диагонали АС.Тогда a 2 -b 2 =
d 2 -c 2 =АМ 2 -СМ 2 =(АМ+СМ)(АМ-СМ)=
АС(АМ-СМ).Так как a 2 +c 2 =b 2 +d 2
a 2 -b 2 =d 2 -c 2 ,то AK-CK=AM-CM
Это равенство выполняется только
в случае,если точки К и М совпадают,то
есть диагонали АС и ВД этого четырехугольника
Доказательство аналогично для невыпуклого


Свойства вписанного в окружность четырехугольника со взаимно перпендикулярными диагоналями.
Вписанный в окружность четырехугольник со взаимно перпендикулярными диагоналями обладает рядом замечательных свойств.
Приведем несколько задач.
Суммы градусных мер дуг,стягиваваемых противоположными сторонами четырехугольника,равны и составляют 180 0 .
По условию АС ВД,значит, треугольник РДС
прямоугольный(рис 2) и РСД+ РДС=90º.
По свойству вписанных углов получим,что
дуги АmД + BnC =180º. Аналогично доказываем,
что дуги ApB+DkC=180º.
2)Сумма квадратов противоположных сторон четырехугольника равна квадрату диаметра описанной около четырехугольника окружность.
Проведем диаметр описанной окружности через одну из вершин четырехугольника,например диаметр DM(рис 3), и соединим точку М с вершинами А и С.Поскольку дуги ͜ DmA+
͜ BnC=180º(см задачу 1) и ͜ DmA + ͜ AlM=180º,то дуги AlM=BnC,а отсюда АМ=ВС.
Из прямоугольного треугольника МАD(MAD =90º) имеем AD 2 +AM 2 =DM 2 ,то есть AD 2 +BC 2 =4R 2 .
Площадь четырехугольника равна полусумме произведений противоположных сторон.
К тому же выводу придем,применив теорему Птолемея:
Поскольку АС ┴ ВD,то S =1/2AC∙BD,а тогда S=1/2(AD∙BC+AB∙DC).
Если четырехугольникABCD вписан в окружность, то произведение его
диагоналей равно сумме произведений его противоположных сторон:
Проведем из точки B отрезок BE до пересечения с диагональю AC таким образом, чтобы CBE = ABD. Углы BCЕ и BDA равны как вписанные, опирающиеся на одну и ту же дугу AB. Тогда треугольники ABD и СBЕ подобны (по двум углам). Отсюда следует, что и, следовательно, далее имеем:
AD . BC = BD . CE. (2)
Подобны также треугольники ABE и DBC, так как ABE = DBC и BAE = BDC.
Отсюда следует, что и затем имеем:
AB . CD = BD . AE. (3)
Сложим соответственно левые и правые части равенств (2) и (3). Получим
AD . BC + AB . CD = BD . CE + BD . AE или
AD . BC + AB . CD = BD . (CE + AE) , то есть
AD . BC + AB . CD = BD . AC, что и требовалось.
Замечание. К этому же можно прийти, введя другие обозначения.
Если АВ = ВС = СD = DА = АС = ВD = , то выберем на диагонали АС точку Е так, чтобы угол СВЕ был равен .
Тогда треугольники СВЕ и DВА подобны.
Из подобия треугольников АВЕ и DВС (углы АВЕ и DВС равны как равносоставленные) получаем АЕ :
Значит, ЕС = АЕ = АЕ + ЕС =АС,
Теорема Птолемея доказана. ◄
(Справедлива и теорема, обратная теореме Птолемея).
4)Если вписанный четырехугольник имеет перпендикулярные диагонали,пересекающиеся в точке М,то прямая,проходящая через точку М и перпендикулярная одной из его сторон,делит противовоположную ей сторону пополам.
Упражнения и задачи для самостоятельного решения
1 Докажите, что если четырехугольник АВСD с перпендикулярным диагоналям вписан в
окружность с центром О, то АОВ + СОD = 180.
2 Докажите, что во вписанном четырехугольнике с перпендикулярными диагоналями
расстояние от центра описанной окружности до стороны равно половине противолежащей
3)Диагонали четырехугольника АВСD,вписанного в окружность радиуса R,
перпендикулярны и пересекаются в точке Р. а) Докажите, что AP 2 + BP 2 + CP 2 + DP 2 = 4R 2 .
б) Найдите сумму квадратов сторон четырехугольника АВСD.
Видео:Диагонали четырёхугольника ABCD, вписанного в окружность, взаимно перпендикулярны. Из вершин В и ССкачать
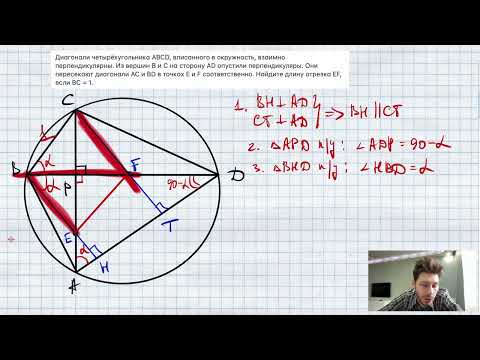
Если диагонали вписанного четырехугольника перпендикулярны
Если диагонали вписанного четырехугольника перпендикулярны, то сумма квадратов его противоположных сторон равна квадрату диаметра описанной окружности.
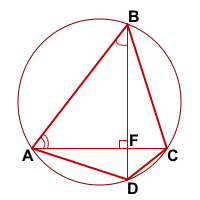
ABCD — вписанный четырёхугольник,
Доказать: AD² +BC² = d²
Радиус и диаметр описанной около треугольника окружности можно найти по формуле
где α — угол, противолежащий стороне a.
Для вписанного треугольника ABD
Для треугольника ABC —
Обозначим точку пересечения диагоналей четырёхугольника ABCD как F.
В прямоугольном треугольнике ABF по определению синуса и косинуса
Что и требовалось доказать.
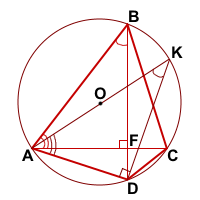
Рассмотрим треугольник ADK.
В прямоугольном треугольнике ABF ∠BAF=90°-∠ABF=90°-∠ABD=90°-∠AKD=∠KAD.
Таким образом, ∪KD=2∠KAD, ∪BC=2∠BAC, ∠BAC=∠KAD. Поэтому ∪KD=∪BC.
Так как дуги равны, то они стягивают равные хорды, то есть KD=BC.
Видео:Четырехугольники, вписанные в окружность. 9 класс.Скачать

Четырехугольники, вписанные в окружность. Теорема Птолемея
 Вписанные четырехугольники и их свойства Вписанные четырехугольники и их свойства |
 Теорема Птолемея Теорема Птолемея |
Видео:3 правила для вписанного четырехугольника #shortsСкачать

Вписанные четырёхугольники и их свойства
Определение 1 . Окружностью, описанной около четырёхугольника, называют окружность, проходящую через все вершины четырёхугольника (рис.1). В этом случае четырёхугольник называют четырёхугольником, вписанным в окружность, или вписанным четырёхугольником .
Теорема 1 . Если четырёхугольник вписан в окружность, то суммы величин его противоположных углов равны 180° .
Доказательство . Угол ABC является вписанным углом, опирающимся на дугу ADC (рис.1). Поэтому величина угла ABC равна половине угловой величины дуги ADC . Угол ADC является вписанным углом, опирающимся на дугу ABC . Поэтому величина угла ADC равна половине угловой величины дуги ABC . Отсюда вытекает, что сумма величин углов ABC и ADC равна половине угловой величины дуги, совпадающей со всей окружностью, т.е. равна 180° .
Если рассмотреть углы BCD и BAD , то рассуждение будет аналогичным.
Теорема 1 доказана.
Теорема 2 (Обратная к теореме 1) . Если у четырёхугольника суммы величин его противоположных углов равны 180°, то около этого четырёхугольника можно описать окружность.
Доказательство . Докажем теорему 2 методом «от противного». С этой целью рассмотрим окружность, проходящую через вершины A , B и С четырёхугольника, и предположим, что эта окружность не проходит через вершину D . Приведём это предположение к противоречию. Рассмотрим сначала случай, когда точка D лежит внутри круга (рис.2).
Продолжим отрезок CD за точку D до пересечения с окружностью в точке E , и соединим отрезком точку E с точкой A (рис.2). Поскольку четырёхугольник ABCE вписан в окружность, то в силу теоремы 1 сумма величин углов ABC и AEC равна 180° . При этом сумма величин углов ABC и ADC так же равна 180° по условию теоремы 2. Отсюда вытекает, что угол ADC равен углу AEC . Возникает противоречие, поскольку угол ADC является внешним углом треугольника ADE и, конечно же, его величина больше, чем величина угла AEC , не смежного с ним.
Случай, когда точка D оказывается лежащей вне круга, рассматривается аналогично.
Теорема 2 доказана.
Перечисленные в следующей таблице свойства вписанных четырёхугольников непосредственно вытекают из теорем 1 и 2.
| Фигура | Рисунок | Свойство | ||||||||||||||||||||||||||||||
| Окружность, описанная около параллелограмма |  | Окружность можно описать около параллелограмма тогда и только тогда, когда параллелограмм является прямоугольником. | ||||||||||||||||||||||||||||||
| Окружность, описанная около ромба |  | Окружность можно описать около ромба тогда и только тогда, когда ромб является квадратом. | ||||||||||||||||||||||||||||||
| Окружность, описанная около трапеции |  | Окружность можно описать около трапеции тогда и только тогда, когда трапеция является равнобедренной трапецией. | ||||||||||||||||||||||||||||||
| Окружность, описанная около дельтоида |  | Окружность можно описать около дельтоида тогда и только тогда, когда дельтоид состоит из двух одинаковых прямоугольных треугольников. | ||||||||||||||||||||||||||||||
| Произвольный вписанный четырёхугольник |  | |||||||||||||||||||||||||||||||
| Окружность, описанная около параллелограмма | ||
 | Окружность можно описать около параллелограмма тогда и только тогда, когда параллелограмм является прямоугольником. | |
| Окружность, описанная около ромба | ||
 | Окружность можно описать около ромба тогда и только тогда, когда ромб является квадратом. | |
| Окружность, описанная около трапеции | ||
 | Окружность можно описать около трапеции тогда и только тогда, когда трапеция является равнобедренной трапецией. | |
| Окружность, описанная около дельтоида | ||
 | Окружность можно описать около дельтоида тогда и только тогда, когда дельтоид состоит из двух одинаковых прямоугольных треугольников. | |
| Произвольный вписанный четырёхугольник | ||
 | ||
| Окружность, описанная около параллелограмма |
 |
Окружность можно описать около параллелограмма тогда и только тогда, когда параллелограмм является прямоугольником.

Окружность можно описать около ромба тогда и только тогда, когда ромб является квадратом.

Окружность можно описать около трапеции тогда и только тогда, когда трапеция является равнобедренной трапецией.

Окружность можно описать около дельтоида тогда и только тогда, когда дельтоид состоит из двух одинаковых прямоугольных треугольников.

Площадь произвольного вписанного четырёхугольника можно найти по формуле Брахмагупты:
где a, b, c, d – длины сторон четырёхугольника,
а p – полупериметр, т.е.
Видео:Если в четырёхугольнике диагонали перпендикулярны ... | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать

Теорема Птолемея
Теорема Птолемея . Произведение диагоналей вписанного четырёхугольника равно сумме произведений противоположных сторон.
Доказательство . Рассмотрим произвольный четырёхугольник ABCD , вписанный в окружность (рис.3).
Докажем, что справедливо равенство:
Для этого выберем на диагонали AC точку E так, чтобы угол ABD был равен углу CBE (рис. 4).
Заметим, что треугольник ABD подобен треугольнику BCE . Действительно, у этих треугольников по два равных угла: угол ABD равен углу CBE (по построению точки E ), угол ADB равен углу ACB (эти углы являются вписанными углами, опирающимися на одну и ту же дугу). Следовательно, справедлива пропорция:
откуда вытекает равенство:
 | (1) |
Заметим, что треугольник ABE подобен треугольнику BCD . Действительно, у этих треугольников по два равных угла: угол ABE равен углу DBC (углы ABD и EBC равны по построению, угол DBE – общий), угол BAC равен углу BDC (эти углы являются вписанными углами, пирающимися на одну и ту же дугу). Следовательно, справедлива пропорция:
📸 Видео
Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

Если в четырёхугольник можно вписать окружностьСкачать

Всё про углы в окружности. Геометрия | МатематикаСкачать

Вписанные четырехугольники. 9 класс.Скачать

Вписанный в окружность четырёхугольник.Скачать

11 класс, 43 урок, Вписанный четырехугольникСкачать

Геометрия Диагонали четырехугольника ABCD вписанного в окружность перпендикулярны, угол ACB = 10Скачать

Четырёхугольник ABCD вписан в окружность ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Четырёхугольник ABCD со сторонами AB = 40 и CD = 10 вписан в окружность. Диагонали #огэ #математикаСкачать

Вписанная и описанная окружность - от bezbotvyСкачать

Урок 2. Описанная окружность около четырехугольника. Задача из ОГЭ| Подобные треугольникиСкачать

ОКРУЖНОСТЬ (вписанный четырехугольник с перпендикулярными диагоналями) ЧАСТЬ 20Скачать

ОГЭ Задание 24 Площадь выпуклого четырехугольника с перпендикулярными диагоналямиСкачать

Задание 26 Вписанный четырёхугольникСкачать
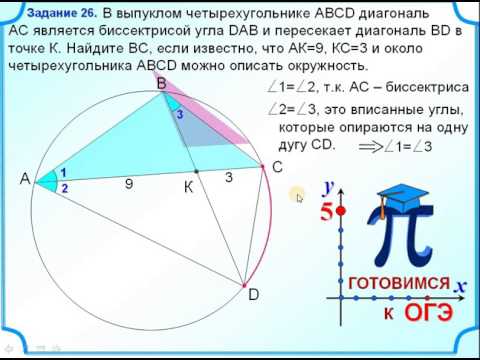
Вписанный четырёхугольник | ЕГЭ-2018. Задание 16. Математика. Профильный уровень | Борис ТрушинСкачать