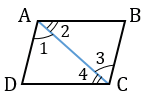
| 1 0 . Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник — параллелограмм. |
Доказательство:
Дано: АВСD — четырехугольник, АD = ВС, АD
Доказать: АВСD — параллелограмм.
Доказательство:
1. Проведем диагональ АС четырехугольника АВСD.
2. Рассмотрим 















3. Итак, АD


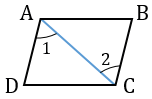
| 2 0 . Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник — параллелограмм. |
Доказательство:
Дано: АВСD — четырехугольник, АВ = DС, АD = ВC.
Доказать: АВСD — параллелограмм.
Доказательство:
1. Проведем диагональ АС четырехугольника АВСD.
2. Рассмотрим 









3. Итак, АD = ВC, АD

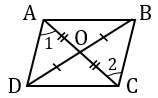
| 3 0 . Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник параллелограмм. |
Доказательство:
Дано: АВСD — четырехугольник, АС и DВ диагонали, АС ∩ DВ = О, АО = ОС, DО = ОВ.
Доказать: АВСD — параллелограмм.
Доказательство:
1. Рассмотрим 








2. 





3. Итак, АD = ВC, АD

Поделись с друзьями в социальных сетях:
Видео:№371. Докажите, что выпуклый четырехугольник ABCD является параллелограммом,Скачать

Как доказать, что четырехугольник — параллелограмм
Как доказать, что четырехугольник — параллелограмм? Для этого можно использовать определение либо один из признаков параллелограмма.
1) Четырехугольник является параллелограммом по определению, если у него противолежащие стороны параллельны, то есть лежат на параллельных прямых.
ABCD — параллелограмм, если
Для доказательства параллельности прямых используют один из признаков параллельности прямых, чаще всего — через внутренние накрест лежащие углы. Для доказательства равенства внутренних накрест лежащих углов можно доказать равенство пары треугольников.
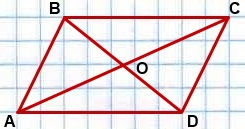
2) Четырехугольник является параллелограммом, если у него диагонали в точке пересечения делятся пополам.
Чтобы использовать этот признак параллелограмма, надо сначала доказать, что AO=OC, BO=OD.
3) Четырехугольник является параллелограммом, если у него противолежащие стороны параллельны и равны.
Чтобы использовать этот признак параллелограмма, надо сначала доказать, что AD=BC и AD ∥ BC (либо AB=CD и AB ∥ CD).
Для этого можно доказать равенство одной из тех же пар треугольников.
Чтобы воспользоваться этим признаком параллелограмма, нужно предварительно доказать, что AD=BC и AB=CD.
Для этого доказываем равенство треугольников ABC и CDA или BCD и DAB.
Это — четыре основных способа доказательства того, что некоторый четырехугольник — параллелограмм. Существуют и другие способы доказательства. Например, четырехугольник — параллелограмм, если сумма квадратов его диагоналей равна сумме квадрату сторон. Но, чтобы воспользоваться дополнительными признаками, надо их сначала доказать.
Доказательство с помощью векторов или координат также опирается на определение и признаки параллелограмма, но проводится иначе. Об этом речь будет вестись в темах, посвященных векторам и декартовым координатам.
Видео:№950. Докажите, что четырехугольник MNPQ является параллелограммом,Скачать

Доказать, что четырехугольник ABCD — параллелограмм, если А (8;-3), В (2;5),
Обосновать, что четырехугольник ABCD — параллелограмм, если А (8;-3), В (2;5), С (10;11), В (16;3). Найти координаты точки скрещения его диагоналей.
- Павел
- Геометрия 2019-07-21 08:18:13 8 1
координаты проекций на оси длина
BC = (10-2;11-5))=(8; 6) ВC=(8^2+6^2)=10
CD = (16-10;3-11))=(6; 8) ВC=(6^2+8^2)=10
длина всех сторон 10
свойство параллелограмма : обратные стороны попарно равны
ДОКАЗАНО
более того — этто ромб ( похож на квадрат)
диагонали -это АС и BD — точка пересечения М
координаты точки скрещения его диагоналей (т . М)
🎬 Видео
Геометрия На рисунке четырехугольник ABCD – параллелограмм, угол BEC = углу DFA. Докажите, чтоСкачать

№933. Найдите координаты вершины D параллелограмма ABCD, если А (0; 0), B (5; 0), С (12; -3.).Скачать

№951. Докажите, что четырехугольник ABCD является прямоугольником, и найдите егоСкачать

№383 На диагонали BD параллелограмма ABCD отмечены две точки Р и Q так, что PB=QD. ДокажитеСкачать

№382. Диагонали параллелограмма ABCD пересекаются в точке О. Докажите, что четырехугольникСкачать

8 класс, 4 урок, ПараллелограммСкачать

№1028. В параллелограмме ABCD AD=7⅓м, BD=4,4 м, ∠A=22°30'. Найдите ∠BDC и ∠DBC.Скачать

№770. Дан параллелограмм ABCD. Выразите вектор АС через векторы а и b , если:Скачать

Доказательство первого признака параллелограммаСкачать

Геометрия В четырех угольнике ABCD известно, что AB ll СD, угол A = угол C. Докажите, что четырехСкачать

№378. Докажите, что параллелограмм является выпуклым четырехугольником.Скачать

№772. Дан параллелограмм ABCD. Докажите, что ХА+ХС=XB+XD, где X— произвольнаяСкачать

8 класс, 5 урок, Признаки параллелограммаСкачать

№331. Пусть ABCD — параллелограмм, а О — произвольная точка пространства.Скачать
Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

2041 четырёхугольник ABCD вписан в окружность угол abd равен 38 угол cаd равен 54 Найдите угол ABCСкачать

Геометрия 8 класс. Параллелограмм, свойства параллелограммаСкачать

§-2 № 1-64 - Геометрия 9 класс Мерзляк углубленный уровеньСкачать