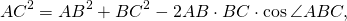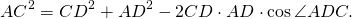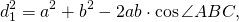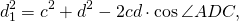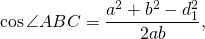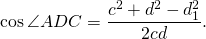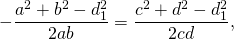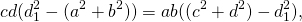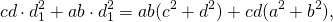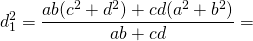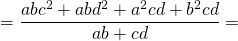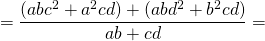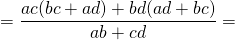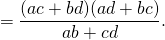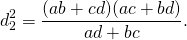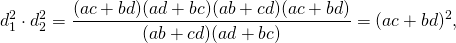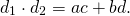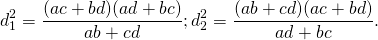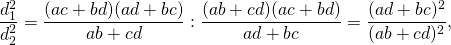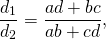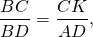Доказательство теоремы птолемея для четырехугольника вписанного

Вписанные четырехугольники и их свойства

Теорема Птолемея

Вписанные четырёхугольники и их свойства

Определение 1 . Окружностью, описанной около четырёхугольника, называют окружность, проходящую через все вершины четырёхугольника (рис.1). В этом случае четырёхугольник называют четырёхугольником, вписанным в окружность, или вписанным четырёхугольником .

Теорема 1 . Если четырёхугольник вписан в окружность, то суммы величин его противоположных углов равны 180° .

Доказательство . Угол ABC является вписанным углом, опирающимся на дугу ADC (рис.1). Поэтому величина угла ABC равна половине угловой величины дуги ADC . Угол ADC является вписанным углом, опирающимся на дугу ABC . Поэтому величина угла ADC равна половине угловой величины дуги ABC . Отсюда вытекает, что сумма величин углов ABC и ADC равна половине угловой величины дуги, совпадающей со всей окружностью, т.е. равна 180° .

Если рассмотреть углы BCD и BAD , то рассуждение будет аналогичным.

Теорема 1 доказана.

Теорема 2 (Обратная к теореме 1) . Если у четырёхугольника суммы величин его противоположных углов равны 180°, то около этого четырёхугольника можно описать окружность.

Доказательство . Докажем теорему 2 методом «от противного». С этой целью рассмотрим окружность, проходящую через вершины A , B и С четырёхугольника, и предположим, что эта окружность не проходит через вершину D . Приведём это предположение к противоречию. Рассмотрим сначала случай, когда точка D лежит внутри круга (рис.2).

Продолжим отрезок CD за точку D до пересечения с окружностью в точке E , и соединим отрезком точку E с точкой A (рис.2). Поскольку четырёхугольник ABCE вписан в окружность, то в силу теоремы 1 сумма величин углов ABC и AEC равна 180° . При этом сумма величин углов ABC и ADC так же равна 180° по условию теоремы 2. Отсюда вытекает, что угол ADC равен углу AEC . Возникает противоречие, поскольку угол ADC является внешним углом треугольника ADE и, конечно же, его величина больше, чем величина угла AEC , не смежного с ним.

Случай, когда точка D оказывается лежащей вне круга, рассматривается аналогично.

Теорема 2 доказана.

Перечисленные в следующей таблице свойства вписанных четырёхугольников непосредственно вытекают из теорем 1 и 2.

Площадь произвольного вписанного четырёхугольника можно найти по формуле Брахмагупты:

где a, b, c, d – длины сторон четырёхугольника,
а p – полупериметр, т.е.

Фигура	Рисунок	Свойство
Окружность, описанная около параллелограмма		Окружность можно описать около параллелограмма тогда и только тогда, когда параллелограмм является прямоугольником.
Окружность, описанная около ромба		Окружность можно описать около ромба тогда и только тогда, когда ромб является квадратом.
Окружность, описанная около трапеции		Окружность можно описать около трапеции тогда и только тогда, когда трапеция является равнобедренной трапецией.
Окружность, описанная около дельтоида		Окружность можно описать около дельтоида тогда и только тогда, когда дельтоид состоит из двух одинаковых прямоугольных треугольников.
Произвольный вписанный четырёхугольник

Площадь произвольного вписанного четырёхугольника можно найти по формуле Брахмагупты:

где a, b, c, d – длины сторон четырёхугольника,
а p – полупериметр, т.е.

Окружность, описанная около параллелограмма
	Окружность можно описать около параллелограмма тогда и только тогда, когда параллелограмм является прямоугольником.
Окружность, описанная около ромба
	Окружность можно описать около ромба тогда и только тогда, когда ромб является квадратом.
Окружность, описанная около трапеции
	Окружность можно описать около трапеции тогда и только тогда, когда трапеция является равнобедренной трапецией.
Окружность, описанная около дельтоида
	Окружность можно описать около дельтоида тогда и только тогда, когда дельтоид состоит из двух одинаковых прямоугольных треугольников.
Произвольный вписанный четырёхугольник

Окружность, описанная около параллелограмма

Окружность можно описать около параллелограмма тогда и только тогда, когда параллелограмм является прямоугольником.

Окружность, описанная около ромба

Окружность можно описать около ромба тогда и только тогда, когда ромб является квадратом.

Окружность, описанная около трапеции

Окружность можно описать около трапеции тогда и только тогда, когда трапеция является равнобедренной трапецией.

Окружность, описанная около дельтоида

Окружность можно описать около дельтоида тогда и только тогда, когда дельтоид состоит из двух одинаковых прямоугольных треугольников.

Произвольный вписанный четырёхугольник

Площадь произвольного вписанного четырёхугольника можно найти по формуле Брахмагупты:

где a, b, c, d – длины сторон четырёхугольника,
а p – полупериметр, т.е.

Теорема Птолемея

Теорема Птолемея . Произведение диагоналей вписанного четырёхугольника равно сумме произведений противоположных сторон.

Доказательство . Рассмотрим произвольный четырёхугольник ABCD , вписанный в окружность (рис.3).

Докажем, что справедливо равенство:

Для этого выберем на диагонали AC точку E так, чтобы угол ABD был равен углу CBE (рис. 4).

Заметим, что треугольник ABD подобен треугольнику BCE . Действительно, у этих треугольников по два равных угла: угол ABD равен углу CBE (по построению точки E ), угол ADB равен углу ACB (эти углы являются вписанными углами, опирающимися на одну и ту же дугу). Следовательно, справедлива пропорция:

откуда вытекает равенство:

(1)

Заметим, что треугольник ABE подобен треугольнику BCD . Действительно, у этих треугольников по два равных угла: угол ABE равен углу DBC (углы ABD и EBC равны по построению, угол DBE – общий), угол BAC равен углу BDC (эти углы являются вписанными углами, пирающимися на одну и ту же дугу). Следовательно, справедлива пропорция:

Теорема Птолемея

Произведение диагоналей вписанного четырёхугольника равно сумме произведений двух пар его противолежащих сторон.

Дано:

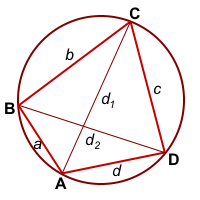
4-угольник ABCD вписан в окр. (O; R)

Из треугольников ABC и ADC по теореме косинусов

Введём обозначения AB=a, BC=b, CD=c, AD=d, AC=d₁, BC=d₂.

Так как четырёхугольник ABCD — вписанный, то ∠ABC+∠ADC=180°.

Что и требовалось доказать.

В ходе доказательства получили полезные соотношения:

1) Диагонали вписанного четырёхугольника связаны с его сторонами равенствами:

2)Отношение диагоналей вписанного четырёхугольника.

то есть диагонали вписанного четырехугольника относятся как суммы произведений сторон, сходящихся в концах диагоналей.

Построим угол CBK, равный углу DBA.

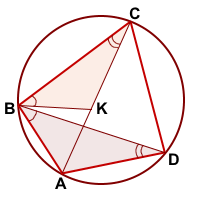
У треугольников CBK и DBA

∠CBK=∠DBA (по построению)

Значит треугольники CBK и DBA подобны (по двум углам).

Из подобия треугольников следует пропорциональность соответствующих сторон:

откуда по основному свойству пропорции

Рассмотрим треугольники ABK и DBC.

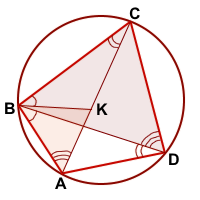
∠BAK=∠BDC (как вписанные углы, опирающиеся на одну дугу BC).

а так как ∠ABD=∠CBK, то и ∠ABK=∠DBC.

Следовательно, треугольники ABK и DBC подобны (по двум углам), и

Проект «Теорема Птолемея для вписанного четырехугольника»

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»

Свидетельство и скидка на обучение каждому участнику

Мною проведено открытое факультативное занятие «Проект «Теорема Птолемея для вписанного четырехугольника» в 11 «А» классе гимназии № 1 г. Ивье. В результате получены положительные отзывы об этом занятии от коллег и администрации гимназии. Учащиеся подготовили и на занятии защитили семь разных доказательств теоремы Птолемея с помощью мультимедийных презентаций. Бегун Татьяна для доказательства теоремы Птолемея использовала подобие треугольников, Пешко Максим – теорему синусов, Гурина Юлия – теорему косинусов (попутно вывела формулу для выражения длины диагонали вписанного четырехугольника через его стороны), Садовский Дмитрий – метод площадей, Дмитриев Никита – педальный треугольник и прямую Симпсона, Ошейчик Мария – преобразование инверсии, Анацкий Денис – теорему Бретшнейдера, представляющую собой теорему косинусов для четырехугольника. Богданович Юлия и Богданович Иван представили свои решения вступительных задач по математике в вузы с использованием теоремы Птолемея. Таким образом, на проведенном факультативном занятии учащиеся углубили свои знания о вписанных четырехугольниках, убедились, что с помощью теоремы Птолемея можно доказать теорему Пифагора, теорему косинусов для треугольника, вывести формулы синуса суммы и синуса разности, что теорема Птолемея до сих пор является источником для множества обобщений и плодотворных идей.

Е сли четырехугольник ABCD (рис. 1) вписан в окружность , то п роизведение его диагоналей равно сумме произведений его противоположных сторон:

AC . BD = AB . CD + AD . BC

Данная теорема установлена Клавдием Птолемеем во втором веке нашей эры.

► Первое доказательство будет в основном следовать доказательству самого Птолемея, приведенному им в книге «Альмагест». Используется подобие треугольников.

На чертеже (рис. 1) изображен данный четырехугольник ABCD , его диагонали АС и В D и описанная около него окружность.

Проведем из точки B отрезок BE до пересечения с диагональю AC таким образом, чтобы  CBE =  ABD . Углы  BC Е и  BDA равны как вписанные, опирающиеся на одну и ту же дугу AB . Тогда треугольники ABD и С BЕ подобны (по двум углам). Отсюда следует, что и , следовательно, далее имеем:

AD . BC = BD . CE . ( 2 )

Подобны также треугольники ABE и DBC , так как  ABE =  DBC и  BAE =  BDC .

Отсюда следует, что и затем имеем:

AB . CD = BD . AE . ( 3 )

Сложим соответственно левые и правые части равенств ( 2 ) и ( 3 ). Получим

AD . BC + AB . CD = BD . CE + BD . AE или

AD . BC + AB . CD = BD . ( CE + AE ) , то есть

AD . BC + AB . CD = BD . AC , что и требовалось .

Замечание. К этому же можно прийти, введя другие обозначения.

Если АВ = ВС = С D = D А = АС = В D = , то выберем на диагонали АС точку Е так, чтобы угол СВЕ был равен .

Тогда треугольники СВЕ и D ВА подобны.

Поэтому ЕС :

Из подобия треугольников АВЕ и D В С (углы АВЕ и D В С равны как равносоставленные) получаем АЕ :

Значит, ЕС = АЕ = АЕ + ЕС =АС,

отсюда

Теорема Птолемея доказана. ◄

(Справедлива и теорема, обратная теореме Птолемея).

►► Второе доказательство. Используется теорема синусов.

Так как четырехугольник вписанный, то кроме входящих в условие теоремы величин целесообразно рассмотреть радиус круга R и углы четырехугольника. Введя углы, мы сможем использовать свойство вписанного четырехугольника.

Итак, пусть и вписанные углы, опирающиеся соответственно на стороны АВ, ВС и А D (рис. 1).

Тогда D ВС = D АС = .

По теореме синусов

.

Следовательно,

Так как ,

то =

Значит, . ◄

►►► Третье доказательство. Используется теорема косинусов.

Пусть АВ = ВС = С D = D А = АС = В D =

Нужно доказать, что

По теореме косинусов имеем:

.

Избавляясь от косинусов и раскладывая на множители, получаем:

,

.

Аналогично, .

Перемножив последние два равенства и произведя соответствующие сокращения, найдем:

,

откуда и следует утверждение теоремы Птолемея. ◄

►►►► Четвертое доказательство. Используется метод площадей.

Будем применять те же обозначения, что и в предыдущем доказательстве.

Найдем площадь S четырехугольника АВС D двумя способами.

Площадь выпуклого четырехугольника равна половине произведения диагоналей на синус угла между ними:

где угол между диагоналями.

Рассмотрим на дуге АВС (рис. 2 ) точку В´ такую, что АВ = СВ´. Поскольку треугольники АВС и СВ´А равны, то равны и их площади. Тогда равны площади четырехугольников АВС D и А В´С D .

Разобьем вновь полученный четырехугольник А В´С D на два треугольника диагональю D В´.

Площадь треугольника А В´ D равна DA В´ ,

площадь треугольника СВ´ D равна DC В´ .

Так как четырехугольник А В´С D вписанный, то углы D А В´ и D С В´ в сумме дают 180º и поэтому синусы этих углов совпадают.

Остается заметить, что

DA В´ = CA В´ =

по теореме об угле между пересекающимися хордами.

Складывая площади треугольников и приравнивая результат к площади четырехугольника, получаем

, откуда ,

что и требовалось доказать. ◄

Замечание. Та же идея может быть реализована по-другому. Покажем возникающие при этом нюансы.

Произведение диагоналей четырехугольника АВС D (рис. 3) равно площади этого четырехугольника S , деленной на 0,5

(как внешний угол треугольника ВОС).

Остается показать, что и

АВ · D С + ВС · D А = S : 0,5.

Для этого заметим, что площадь четырехугольника АВС D не изменится, если треугольник ВС D «перевернуть», поменяв местами вершины В и D (рис. 4).

Тогда

После этого учтем, что в полученном четырехугольнике сумма противоположных углов равна 180º, т. е.

º, откуда следует,

что и

АС · D В =АВ · D С + ВС · D А.

►►►►► Пятое доказательство . Используется прямая Симпсона.

Здесь потребуются некоторые дополнительные сведения из геометрии треугольника.

Определим такое понятие как педальный треугольник. Пусть Р – любая точка внутри треугольника АВС, и пусть перпендикуляры, опущенные из точки Р на его стороны ВС = , СА = , АВ = будут .

Тогда треугольник , вершинами которого являются основания этих перпендикуляров, называется педальным треугольником точки Р относительно треугольника АВС

(например, треугольник с вершинами в точках касания вписанной окружности со сторонами данного треугольника – педальный треугольник центра вписанной окружности).

Прямые углы в точках и (рис. 5) указывают на то, что эти точки лежат на окружности с диаметром АР;

другими словами, точка Р лежит на окружности, описанной вокруг треугольника .

Применяя теорему синусов к этому треугольнику, а также к самому треугольнику АВС, получим

откуда Аналогично, и

Таким образом, если расстояния от педальной точки до вершин треугольника АВС равны то длины сторон педального треугольника равны соответственно

Теперь рассмотрим тот особый случай, когда точка Р лежит на описанной окружности вокруг треугольника АВС (рис. 6).

Тогда педальный треугольник «вырождается» в прямую, называемую прямой Симпсона.

Хотя «педальный треугольник» вырожден, длины его «сторон» все еще могут быть вычислены с помощью формул:

, ,

Так как , то , т. е.

АВ · СР + ВС · АР = АС · ВР.

Так как АВСР – вписанный четырехугольник, то таким образом мы доказали теорему Птолемея. ◄

►►►►►► Шестое доказательство. Используется преобразование, которое называется инверсией.

Пусть задана некоторая окружность S с центром О и радиусом r (рис. 7).

Каждой точке Х, отличной от точки О, поставим в соответствие точку Х´ на луче ОХ, такую, что ОХ´·ОХ = .

Это преобразование и называется инверсией относительно окружности S .

Лемма (об инверсии). Пусть А´ и В´ − образы точек А и В при инверсии с центром О и радиусом r .

Тогда треугольники ОАВ и ОВ´А´ подобны и (рис.8).

Приведем рассуждения, доказывающие утверждение леммы.

По определению инверсии выполняются равенства , .

Следовательно, , и поэтому

Значит, треугольники ОАВ и ОВ´А´ подобны (имеют общий угол при вершине О и их стороны, идущие от этой вершины, пропорциональны).

При этом вершине А соответствует вершина В´, а вершине В – вершина А´.

Но тогда и

Из этого равенства имеем:

Подставляя сюда выражение из определения , получаем Лемма доказана.

Итак, пусть четырехугольник АВС D вписан в окружность S (рис. 9).

По теореме об инверсии эту окружность инверсия I с центром в точке D (и любым радиусом) переведет в прямую p , не проходящую через точку D .

Точки лежат на прямой p ,

причем точка лежит на отрезке .

Поэтому .

По лемме об инверсии

.

Подставив эти выражения в равенство , получаем:

АС · D В = АВ · D С + ВС · D А,

что и требовалось доказать. ◄

Приведенные доказательства на самом деле не исчерпывают всех возможных доказательств теоремы Птолемея.

Седьмое доказательство Теорема Птолемея может быть, например, получена и как следствие теоремы Бретшнейдера (теоремы косинусов для четырехугольника), которая утверждает следующее.

Квадрат произведения диагоналей выпуклого четырехугольника равен сумме квадратов произведений его противоположных сторон без удвоенного произведения всех четырех сторон четырехугольника и косинуса суммы двух его противолежащих углов,

т. е. ,

где угол, равный сумме углов А и С или В и D ,

так как .

Поскольку во вписанном четырехугольнике сумма двух противоположных углов равна 180º, то по теореме Бретшнейдера в этом случае

или , т. е. .

Эта теорема понадобилась Клавдию Птолемею (ок.100 – ок.178) – знаменитому древнегреческому астроному и математику, жившему в Александрии, для составления таблицы синусов, точнее, таблицы длин хорд.

Если АС – диаметр окружности, то теорема Птолемея перепишется в виде

;

если же в качестве диаметра взять сторону АВ, то получим формулу для синуса разности этих углов (рис. 10).

Именно эти частные случаи использовал Птолемей для составления своих таблиц, очень нужных для астрономических расчетов.

В эпоху средневековья книга Птолемея, в которой содержались обширные сведения по астрономии, получила распространение в странах арабского Востока; астрономы называли ее там «Аль Маджисти» − «Величайшее», отсюда и происходит ее название «Альмагест».

Заметим, что если около выпуклого четырехугольника нельзя описать окружность, то произведение его диагоналей меньше суммы произведений противоположных сторон. Докажем это.

Пусть для определенности в данном четырехугольнике АВС D АВС + А D С D лежит вне окружности, проведенной через вершины А, В и С.

Пусть D ВС АВ D .

Построим (как на рис. 11) СВК = АВ D , ВСК = А D В и проведем отрезок АК.

Тогда

, а поэтому

(4)

Следовательно, А D · ВС = В D · КС. (5)

Так как D ВС = АВК,

а из (4) следует, что , то

.

Из подобия этих треугольников вытекает, что ,

АВ · С D = В D · АК. (6)

Сложив (5) и (6) получаем:

А D · ВС + АВ · С D = В D (АК + КС). (7)

Но точка К не лежит на прямой АС, поскольку ВСК, равный А D В, имеющему вершину вне круга, меньше вписанного угла АСВ.

Поэтому из (7) и (8) имеем:

АС · В D · BC + AB · CD.

Значит, для любого выпуклого четырехугольника АВС D имеет место неравенство

Рассмотрим теперь теорему, представляющую обобщение теоремы Птолемея.

В ней речь пойдет о четырех окружностях, касающихся внутренним (внешним) образом некоторой окружности в вершинах вписанного в нее четырехугольника.

Вместо расстояния между двумя вершинами А и В принимается касательное расстояние между соответствующими двумя окружностями , .

Под касательным расстоянием подразумевается расстояние между двумя точками касания общей внешней касательной этих двух окружностей (рис. 12).

Если окружности , , , касаются окружности внутренним (внешним) образом в вершинах А, В, С, D выпуклого четырехугольника АВС D , вписанного в , то касательные расстояния между парами окружностей связаны соотношением:

·+·=·.

Замечание. Если , , , − окружности нулевого радиуса, то получаем обычную теорему Птолемея.

Прежде чем непосредственно перейти к доказательству обобщенной теоремы Птолемея, вычислим касательное расстояние между окружностями и , если дана окружность (О, R ) и две каса ющиеся ее внутренним образом в точках А и В окружности и .

Пусть общая внешняя касательная касается в точке , а − в точке (рис. 13).

Тогда ,

где .

Далее, , где .

Из записанных уравнений следует после исключения и равенство

или, после преобразований,

.

Теперь докажем обобщенную теорему Птолемея.

Впишем в окружность четырехугольник АВС D и построим четыре окружности , , , , касающиеся внутренним образом в точках А, В, С, D (рис. 14).

Тогда согласно полученной формуле имеем:

, ,

, ,

, .

Подставим эти выражения для

, , , ,,

·+=.

В результате получим равенство, равносильное следующему:

АС · D В = АВ · D С + ВС · D А,

что верно для четырехугольника АВС D по обычной теореме Птолемея.

Тем самым, ввиду равносильности соответствующих равенств, обобщенная теорема Птолемея доказана для четырех окружностей, касающихся внутренним образом.

Она же остается в силе и для четырех окружностей, касающихся внешним образом (рис. 15).

Отличие здесь только в том, что если две окружности и касаются внешним образом, то

.

В качестве геометрического практикума по применению теоремы Птолемея решим с ее помощью задачи.

1 . Из концов диаметра, равного 25 см, проведены по одну сторону от него две хорды длиной 24 см и 20 см. Определите расстояние между концами хорд, не лежащими на диаметре.

► Имеем: АВ = 25 см, АС = 24 см, В D = 20 см, АСВ = А D В = 90º (рис. 16). Из треугольника А D В по тереме Пифагора А D = =15(см). Аналогично из треугольника АВС получаем: ВС = = 7 (см).

Введем обозначения: ВО = х, D О = 20 – х, СО = у,

АО = 24 – у. По свойству пересекающихся хорд (АС и В D ):

Из прямоугольного треугольника ОСВ: . Решаем систему уравнений:

Из второго уравнения последней системы находим: у = 5, 25, т. е. СО = 5, 25 см, тогда х = 8, 75, т. е. ВО = 8, 75 см.

Треугольники D ОС и АОВ подобны ( D ОС = АОВ как вертикальные, В D С = ВАС как вписанные и опирающиеся на одну и ту же дугу). Значит, . Отсюда D С = 15 см. ◄

►► Используется теорема Птолемея.

Имеем: АВ = 25 см, АС = 24 см, В D = 20 см, АСВ = А D В = 90º (рис. 16).

Из треугольника А D В по тереме Пифагора А D = =15(см). Аналогично из треугольника АВС получаем: ВС = = 7 (см).

Четырехугольник АВС D – вписанный.

По теореме Птолемея

АС · D В = АВ · D С + ВС · D А, т. е.

24 · 20 = 15 · 7 + 25 · D С. Отсюда D С = 15 см.

2 . Четырехугольник АВС D вписан в окружность, причем АС D = 90º, АСВ = ВА D , А D = 2, С D = . Найдите ВС.

► Используется теорема Птолемея.

Из условия следует, что А D – диаметр, АВ D = 90º, АВ = В D (рис. 17). Следовательно, треугольник АВ D – равнобедренный прямоугольный, откуда АВ = В D = . Далее, из прямоугольного треугольника АС D находим катет АС. Он равен 8/5. Осталось применить теорему Птолемея: .

Ответ: . ◄

►► Установив, что АВ = , АС = 8/5, АСВ = 45º (см. первое решение), дальше применим теорему косинусов (, (рис. 17)): . Решая полученное квадратное уравнение, найдем два его корня: . Один из них посторонний, так как по условию ВС ◄

📹 Видео