Доказать что bc параллельно ad четырехугольника abcd

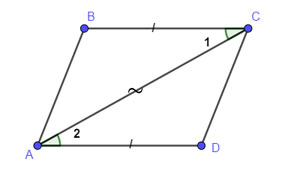
Если в четырёхугольнике две противолежащие стороны равны и параллельны, то этот четырёхугольник — параллелограмм.

Доказательство.

На рисунке изображён четырёхугольник ABCD, в кото­ром ВС = AD и ВС AD . Докажем, что четырёх­угольник ABCD —параллелограмм. В треугольниках ABC и ACD имеем: ВС = AD по условию, углы 1 и 2 равны как накрест лежащие при параллельных прямых ВС и AD и секущей AC , а сторона AC — общая . Следовательно, треугольники ABC и ACD равны по первому признаку равенства треугольников. Отсюда АВ = СD . Значит, в четырёхугольнике ABCD каждые две противолежащие стороны равны .

Поэтому четырёхугольник ABCD — параллелограмм.

Докажите теорему:

Если в четырёхугольнике две противолежащие стороны равны и параллельны, то этот четырёхугольник — параллелограмм.

Доказательство.

На рисунке изображён четырёхугольник ABCD, в кото­ром ВС =______и ВС ΙΙ_____. Докажем, что четырёх­угольник ABCD —__________________________________. В треугольниках ABC и________имеем: ВС = по условию, углы 1 и______равны как___________при параллельных прямых ВС и _____ и секущей______, а сторона АС-______________. Следовательно, треугольники ABC и ______ равны по ________________________ признаку равенства треугольников. Отсюда АВ = _________. Значит, в четырёхугольнике ABCD каждые две противолежащие стороны_________________

Поэтому четырёхугольник ABCD — параллелограмм.

Видео:№371. Докажите, что выпуклый четырехугольник ABCD является параллелограммом,Скачать

В четырехугольнике ABCD ВС = AD и ВС || AD; ∠BAC + ∠ACD — 80°. Найдите эти углы

Видео:№47. В пространственном четырехугольнике ABCD стороны АВ и CD равны. Докажите, что прямые АВ и CDСкачать

Ваш ответ

Видео:№172. На рисунке 96 AC=AD, AB⊥CD. Докажите, что BC=BD и ∠ACB=∠ADB.Скачать

решение вопроса

Видео:№951. Докажите, что четырехугольник ABCD является прямоугольником, и найдите егоСкачать

Похожие вопросы

• Все категории
• экономические 43,277
• гуманитарные 33,618
• юридические 17,900
• школьный раздел 606,680
• разное 16,822

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Видео:№751. Определите вид четырехугольника ABCD, если:Скачать

Как доказать, что четырехугольник является параллелограммом?

Согласно определению,геометрическая фигура параллелограмм является четырехугольником с попарно параллельными противоположными сторонами и равными противолежащими углами. Доказать, что фигура параллелограмм позволяет как определение, так и ее признаки. Применяя на практике эти свойства, можно решать геометрические задачи разной сложности.

Видео:№189. Используя данные рисунка 108, докажите, что BC||AD.Скачать

Определение параллелограмма

Четырехугольник является параллелограммом с параллельными противоположными сторонами. Эта фигура имеет по 2 тупых и острых угла, произвольную величину которых определяют при решении задач. Для этого используют не только признаки параллелограмма или треугольника, но и таблицу синусов с косинусами.

Квадрат, прямоугольник и ромб — это параллелограммы, обладающие общими свойствами. Фигура, у которой диагонали совпадают с биссектрисами, является ромбом. Согласно определению, прямоугольник — это четырехугольник, имеющий все прямые углы. Если стороны этой фигуры равны между собой, то прямоугольник является квадратом.

Параллелограмм — геометрическая фигура с равными противоположными сторонами. Если каждую из них возвести в квадрат и сложить их между собой, то полученная величина будет равна сумме квадратов диагоналей, проведенных через противоположные вершины углов фигуры. Диагонали этого четырехугольника пересекаются в точке, определить которую позволяют прямоугольные координаты.

Видео:Геометрия Сторона AD четырехугольника ABCD является диаметром окружности, описанной около негоСкачать

Свойства фигуры

Зная различные свойства четырехугольников, можно решать простые и сложные задачи по геометрии, начиная с определения периметра, заканчивая нахождением координаты вершины параллелограмма. Для решения задач используют 7 основных свойств параллелограмма, учитывая что его стороны попарно образуют:

• смежные углы, сумма которых составляет 180 градусов;
• равные отрезки;
• одинаковые по величине противоположные углы;
• четырехугольник, сумма углов которого равна 360 градусов;
• фигуру, диагонали которой пересекаются в точке, разделяющей их на 2 равных отрезка;
• равнобедренный треугольник, одна из сторон которого является биссектрисой фигуры;
• симметричные фигуры, дополняемые линией, проходящей через точку пересечения диагоналей.

Доказать последнее свойство позволяет II признак равенства треугольников. Известен отрезок, принадлежащий линии, проведенной через точку, в которой пересекаются диагонали. В четырехугольнике КМРТ он обозначен НП. Отсюда следует равенство треугольников КОП и НОР, поэтому НО=ОП.

Сумма смежных углов параллелограмма составляет 180 градусов, поскольку они являются односторонними при параллельных прямых. Существует свойство равенства острого угла и образованного высотами тупого угла четырехугольника АВСД. Параллелограмм имеет смежные углы А и Д, а высоты ВМ и ВН проведены из вершины В, поэтому угол МВН в сумме с Д равен 180 градусам.

Доказательство равенства противолежащих сторон и углов фигуры заключается в следующем. Например, диагонали ABCD делят фигуру на 2 равных треугольника, имеющих общую сторону в виде диагонали BD. При этом углы ADВ и ABC при противолежащих вершинах A и C являются накрест лежащими.

Параллелограмм состоит из равных треугольников ABD, BCD и ABC, ACD, образуемых диагоналями AC и ВD, значит AB=CD и AD=BC. Отсюда углы при вершинах A и C, В и D имеют одинаковую величину.

Свойства можно представить в виде формул для решения уравнений и примеров, а также доказать теоретически. Их следует запомнить, чтобы правильно применять на практике. Для решения более сложных задач по геометрии следует доказать основные свойства фигуры.

Видео:№369. Найдите углы A, B и C выпуклого четырехугольника ABCD, еслиСкачать

Основные признаки

Существует 5 признаков параллелограмма, доказательство которых основано на свойствах прямых и образованных ими углов либо фигур. Выпуклый четырехугольник, вершины которого обозначены МНКП, имеет диагонали МП и НК. Признаки того, что фигура МНКП представляет собой параллелограмм, следующие:

• попарное равенство противоположных сторон: МН=КП и НК=МП;
• попарное равенство противоположных углов: МНК=КПМ и НКП=НМП;
• равенство и параллельность противоположных сторон: МН=КП и МН||КП;
• пересечение диагоналей в точке, которая делит их пополам;
• МН2 + КП2 = МН2 + НК2 + КП2 + МП2

Если четырехугольник имеет 2 равные и параллельные стороны, то он представляет собой параллелограмм. Четырехугольник MNPK имеет параллельные и равные MN и KP, отсюда следует доказательство I признака:

Параллельность других сторон MK и NP при диагонали MP основана на равенстве накрест лежащих углов, поэтому четырехугольник MNPK — параллелограмм.

Если четырехугольник имеет противоположные стороны, которые равны попарно, то он является параллелограммом. Перед тем как доказать, что фигура является параллелограммом, следует провести диагонали. Пошаговое доказательство II признака:

Доказать деление точкой пересечения каждой из диагоналей фигуры АМКД на равные отрезки позволяет II признак равенства треугольников. При этом AОД и КОМ равны. Следовательно, AО=КО и АО=ДО.

Согласно III признаку, четырехугольник, диагонали которого пересекаются, а точка пересечения делит их пополам, представляет собой параллелограмм. В четырехугольнике MNPQ она обозначена буквой К. Поскольку в ней пересекаются диагонали MP и NQ, то образуемые ими треугольники MNК и КPQ равны по I признаку. Это следует из равенства вертикальных углов MКN и PКQ, а также MК и NК, КP и КQ, которые равны по условию.

В треугольниках MNК и КPQ стороны MN и PQ равны между собой. Углы NMК и КPQ равны как накрест лежащие при MN и PQ и секущей MP. Отсюда следует, что прямые MN||PQ. Итак, четырехугольник MNPQ — это параллелограмм по I признаку, поскольку MN и PQ равны и параллельны.

Видео:✓ Задача про комплексное число | Ботай со мной #101 | Борис ТрушинСкачать

Пошаговое доказательство

Перед тем как доказать, что четырехугольник параллелограмм, нужно провести высоты треугольников МНК и МПК, пересекающие МК в точках О и С. По данным задачи, МНК, МПК и НПК имеют одинаковые площади. Доказательство параллельности МК и НП состоит из следующих шагов:

Отсюда следует, что МК и НП — параллельны.

Чтобы доказать, что МН и ПК параллельны, нужно опустить из вершин треугольников МНК и НКП высоты Н и П, которые пересекут прямую ПК в точках Р и Т. По построению НР=ПТ, а по указанному условию площади треугольников МНК и НПК совпадают. Сторона МН параллельна ПК, следовательно, МНПК — параллелограмм. Итак, порядок доказательства параллельности МН и ПК аналогичен с доказательством, что МК и НП параллельны.

Доказательство признака образования равнобедренного треугольника и трапеции при пересечении противолежащей стороны параллелограмма биссектрисой АМ одного из углов состоит из следующих утверждений:

Зная, как доказать, что фигура параллелограмм, если известно, что 2 из его сторон равны и параллельны, можно использовать I признак равенства для доказательства другого. Согласно II признаку, стороны параллелограмма попарно равны между собой.

🌟 Видео

№137. На рисунке 53 (с. 31) BC=AD, AB = CD. Докажите, что ∠B=∠D.Скачать

№199. Прямая р параллельна стороне АВ треугольника ABC. Докажите, что прямые ВССкачать

№190. На рисунке 109 АВ=BC, AD=DE, ∠C=70°, ∠EAC = 35°. Докажите, что DE||АС.Скачать

SOS-ГЕОМЕТРИЯ! Отрезки и углы, смежные и вертикальные углы | Математика TutorOnlineСкачать

ВСЯ ГЕОМЕТРИЯ ИЗ ОГЭ ПО МАТЕМАТИКЕ 2023 ЗА 40 МИНУТСкачать

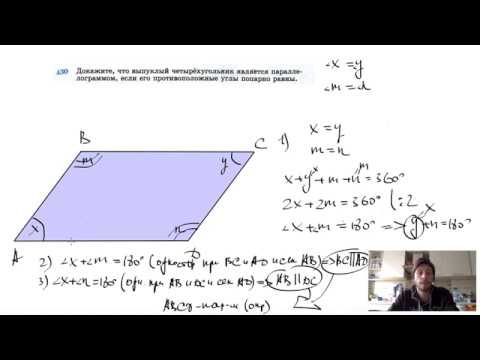
№430. Докажите, что выпуклый четырехугольник является параллелограммом, если его противоположныеСкачать

Геометрия На рисунке четырехугольник ABCD – параллелограмм, угол BEC = углу DFA. Докажите, чтоСкачать

Все про ПАРАЛЛЕЛОГРАММ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // ГеометрияСкачать

№117. В тетраэдре ABCD известно, что BC⊥AD. Докажите, что AD⊥MN, где М и N — середины реберСкачать

Геометрия В четырёхугольнике ABCD (см. рис.) угол C=110, угол D=70. Докажите, что BC II AD.Скачать

Параллельные прямые | Математика | TutorOnlineСкачать