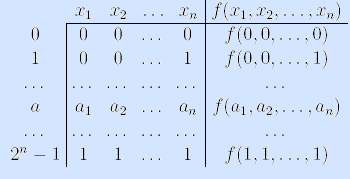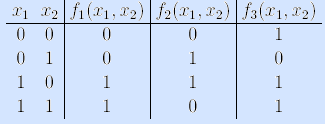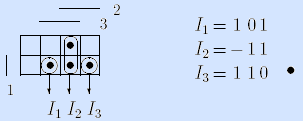Для функции заданной вектором значений (8 видео)

Для функции заданной вектором значений

1) Задание булевой функции таблицей истинности. Так называется таблица, состоящая из двух частей: в левой части перечисляются все наборы значений аргументов (булевы векторы пространства B n ) в естественном порядке, то есть по возрастанию значений чисел, представляемых этими векторами, а в правой части – значения булевой функции на соответствующих наборах.

Пример. Рассмотрим булеву функцию трех аргументов, называемую мажоритарной (или функцией голосования): она принимает значение 1 на тех и только тех наборах, в которых единиц больше, чем нулей (major – больший).

Так как левая часть таблицы истинности постоянна для всех функций с одинаковым числом аргументов, несколько таких функций могут быть заданы общей таблицей.

Теорема о числе булевых функций. Число различных булевых функций, зависящих от n переменных, равно 2 2 n .

Доказательство. Каждая булева функция определяется своим столбцом значений. Столбец является булевым вектором длины m=2 n , где n – число аргументов функции. Число различных векторов длины m (а значит и число булевых функций, зависящих от n переменных) равно 2 m =2 2 n . •

2) Задание булевой функции характеристическими множествами. Так называются два множества:

M 1 _f, состоящее из всех наборов, на которых функция принимает значение 1, то есть M 1 _f = <α B n :f(α) = 1>;

M 0 _f, состоящее из всех наборов, на которых функция принимает значение 0, то есть M 0 _f = <α B n :f(α) = 0>.

Пример (мажоритарная функция).

3) Задание булевой функции вектором ее значений.

Пример (мажоритарная функция).

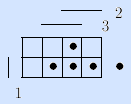
4) Задание булевой функции матрицей Грея. Булево пространство задается матрицей Грея, и наборы (клетки матрицы), на которых булева функция f(x₁, …, x_n) принимает значение 1, отмечаются и называются точками.

Пример (мажоритарная функция).

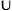
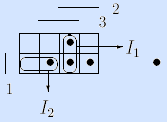
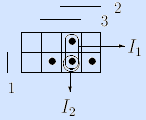
5) Интервальный способ задания булевой функции. Булеву функцию f(x₁, …, x_n) можно задать множеством интервалов I_f = <I₁, I₂, …, I_k>, объединение которых образует характеристическое множество M 1 _f, то есть I₁ I₂… I_k = M 1 _f. Множество интервалов I_f называется достаточным для функции f(x₁, …, x_n).

Пример. Мажоритарная функция может быть задана достаточным множеством I_f = <I₁, I₂, I₃> интервалов:

Здесь интервалы представлены троичными векторами и изображены на матрице Грея.

В отличие от предыдущих, интервальный способ задания функций многовариантен (одну и ту же булеву функцию можно представить разными множествами интервалов).

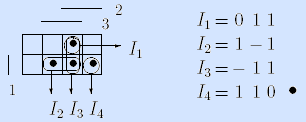
Пример. Зададим мажоритарную функцию другим достаточным множеством I’_f = <I₁, I₂, I₃, I₄> интервалов:

Очевидно, что это множество интервалов избыточно: первый интервал (011) можно удалить.

Определение. Интервал назовем допустимым для булевой функции, если на всех его наборах функция равна 1.

Примеры. I₁= – 1 1 – допустимый интервал для мажоритарной функции, I₂= 1 0 – – не допустимый.

Определение. Интервал I назовем максимальным для булевой функции f(x₁, …, x_n), если он является допустимым для этой функции, и не существует другого допустимого интервала I’, такого что I 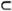I’.

Пример. I₁= –11 является максимальным интервалом для мажоритарной функции, а допустимый интервал I₂ = 111 не является максимальным, так как I₂ 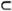I₁.

Пример. Зададим мажоритарную функцию множеством I»_f = <I₁ I₂, I₃> всех максимальных интервалов.

Определение. Точку булевой функции f(x₁, …, x_n) назовем ядерной, если она принадлежит ровно одному максимальному для этой функции интервалу. Максимальный интервал называется ядерным, если он содержит ядерную точку.

Пример. Для мажоритарной функции ядерными точками являются 011 (принадлежит только интервалу –11), 101 (принадлежит только интервалу 1 –1) и 110 (принадлежит только интервалу 11 –). Все максимальные интервалы этой функции являются ядерными. •

Очевидно, что все ядерные интервалы входят в любое достаточное множество функции, состоящее из максимальных интервалов.

6) Задание булевой функции формулами будет рассмотрено несколько позже.

Содержание

Упражнение № 8. Сокращенная дизъюнктивная нормальная форма для заданных вектором значений функций булевой алгебры
Решение. Для удобства приведем таблицу истинности
Главная > Решение
🎥 Видео

Видео:Булевы функции и способы их заданияСкачать

Упражнение № 8. Сокращенная дизъюнктивная нормальная форма для заданных вектором значений функций булевой алгебры

Для функций булевой алгебры (табл. 22), заданных вектором значений, запишите СДНФ (СКНФ), определите сокращенную дизъюнктивную нормальную форму (сокр. ДНФ). Реализуйте в PC WorX СДНФ (СКНФ) и сокр. ДНФ функции булевой алгебры F.

Вектор значений функции булевой алгебры

Функция булевой алгебры

Проверьте составленную в PC WorX программу в режиме отладки.

Пример выполнения упражнения № 8

Рассмотрим вариант № 30. Таблица истинности, соответствующая функции булевой алгебры F = (01100100), представляет собой таблицу следующего вида (табл. 23).

Таблица истинности F = (01100100)

Для составления формулы в виде СДНФ для функции булевой алгебры, не соответствующей тождественно ложной (противоречию) булевой функции, необходимо выбрать выражения, соответствующие строкам, где функции булевой алгебры истинны, и соединить их операцией v, при этом если в какой-либо строке логическая переменная имеет ложное значение, то в соответствующем выражении она используется с инверсией (в табл. 24 показаны всевозможные «навешивания» инверсии над логическими переменными для построения СДНФ).

Таблица истинности для СДНФ

Составим СДНФ функции булевой алгебры F, заданной вектором значений (01100100): для этого обратим внимание, что эта функция истинна (содержит единицы) в строках под номерами 2, 3 и 6, поэтому выражения из таблицы 24 х Ay az, х Ay az и х Ay az соединяем операцией v:

Lx Л у A zІХ Л у A z I v ІХ А у A Z

Обозначим полученную СДНФ через F1.

Для составления формулы в виде СКНФ для функции булевой алгебры, не соответствующей тождественно истинной (тавтологии) булевой функции, необходимо выбрать выражения, соответствующие строкам, где функции булевой алгебры ложны, и соединить их операцией л, при этом если в какой-либо строке логическая переменная имеет истинное значение, то в соответствующем выражении она используется с инверсией (в табл. 25 показаны всевозможные выражения для построения СКНФ).

Таблица истинности для СКНФ

Составим СКНФ функции булевой алгебры F, заданной вектором значений (01100100): для этого обратим внимание, что эта функция ложна (содержит нули) в строках под номерами 1, 4, 5, 7 и 8, поэтому выражения из таблицы 25 х v у v z , х v у v z , xv у v z , x v у v z и x v у v z соединяем операцией л:

(х V у V z) л [х V у V z)a (х V у V z)a (х V у V z)a (х V у V z

Обозначим полученную СКНФ через F2.

Для построения сокращенной ДНФ, которую обозначим через F3, раскрываем скобки в СКНФ F2, начиная перемножение со скобок, которые отличаются всего одной переменной (например, z и z ).

Поменяв местами вторую и третью скобки и используя законы коммутативности, получим:

(х V у V z) Л (х V у V z) А (х V у V Zj А (х V у V ZJ А (х V у V Z

Перемножим первую и вторую скобки, а также четвертую и пятую скобки:

^ХХ V xy V xz v ух V уу V yz V ZX V zy V ZZJ A |X V у V Z л (xx v xy v xz. v yx v у у v yz v z.x v z.y V ZZ ) •

Воспользуемся законами идемпотентности и хх — 0.

Д v xy V xz v ух V у V yz V zx V zy v zІХ V у V z) A A (x V xy V xz v yx V у V yzv ZXV zyvO).

В первой скобке слагаемое у поглощает все слагаемые, содержащие у, а слагаемое z поглощает все слагаемые, содержащие z. В третьей скобке слагаемое х поглощает все слагаемые, содержащие х, а слагаемое у поглощает все слагаемые, содержащие у . Получим

(у v z) А (х V у V z) А (х V у).

Перемножим вторую и третью скобки:

(у V z) л (хх V ух V Z.X v xy V у у V zy).

Снова воспользуемся законами идемпотентности, дополнения и поглощения. Получим:

(у V z) А (о V ух V ZX V xy V у V zy) = (у v z) a (zX V у).

Перемножаем оставшиеся скобки:

(у V z)a(zX V у) = yz.X V Z.Z.X V у у V zy = У ZX V О V О V zy = yZXV zy ?

Получена сокращенная ДНФ F3 = xyz v yz функции булевой алгебры F.

На рис. 23 представлены примеры построения СДНФ F1, СКНФ F2 и сокр. ДНФ F3 для варианта задания № 30 из табл. 22.

Рис. 23. Тестовый пример булевой алгебры для упражнения № 8: а — СДНФ; б — СКНФ; в — сокр. ДНФ

Для проверки правильности реализации программ с выходными переменными Fl, F2 и F3 используем таблицу истинности (табл. 23): при предъявлении набора входов выходы со всех функций Fl, F2 и F3 будут одинаковые, например, набор (1,0, 1), соответствующий 6 строке таблицы истинности, имеет значение, равное 1, введя указанный набор на входы Fl, F2 и F3, получаем также 1. Аналогично проверяются оставшиеся наборы входов. Таким образом, можно сделать вывод о том, что правильно определена сокращенная ДНФ F3 и реализованы программы для СДНФ F1, СКНФ F2 и сокр. ДНФ F3.

Видео:Для булевой функции, заданной вектором значений, определитьСкачать

Решение. Для удобства приведем таблицу истинности

Главная > Решение

Информация о документе
Дата добавления:
Размер:
Доступные форматы для скачивания:

Для булевой функции, заданной вектором значений (01000000), определить:

1) существенные и фиктивные переменные; (уже сделано)

2) совершенную дизъюнктивную нормальную форму; (уже сделано)

3) совершенную конъюнктивную нормальную форму; (уже сделано)

4) полином Жегалкина двумя способами; (сделан только один способ)

5) принадлежность классам T0,T1, S, M, L

Для удобства приведем таблицу истинности

Проверим, является ли переменная существенной или фиктивной. Рассмотрим значения функции на наборах, соседних по переменной :

f (0,0,0) = 0, f (0,1,0) = 0, f (0,0,1) = 0, f (0,1,1) = 0,

f (1,0,0) = 0. f (1,1,0) = 0. f (1,0,1) = 0. f (1,1,1) = 0.

На всех парах соседних по переменной наборов значений переменных функция принимает равные значения, следовательно, переменная – фиктивная.

Рассмотрим теперь значения функции на наборах, соседних по переменной:

f (0,0,0) = 0, f (1,0,0) = 1, f (0,0,1) = 0, f (1,0,1) = 0,

f (0,1,0) = 0. f (1,1,0) = 0. f (0,1,1) = 0. f (1,1,1) = 0.

Здесь f (1,0,0) ≠ f (1,1,0). Следовательно, переменная – существенная.

Рассмотрим значения функции на наборах, соседних по переменной :

f (0,0,0) = 0, f (1,0,0) = 1, f (0,1,0) = 0, f (1,1,0) = 0,

f (0,0,1) = 0. f (1,0,1) = 0. f (0,1,1) = 0. f (1,1,1) = 0.

Здесь f (1,0,0) ≠ f (1,0,1). Следовательно, переменная – существенная.

Для построения совершенной дизъюнктивной нормальной формы необходимо каждому единичному значению булевой функции поставить в соответствие элементарную конъюнкцию, а конъюнкции соединить дизъюнкцией. Т.е. согласно таблице истинности пункта 1 получим, что СДНФ данной функции примет вид

Для построения совершенной конъюнктивной нормальной формы необходимо каждому нулевому значению булевой функции поставить в соответствие элементарную дизъюнкцию, а дизъюнкции соединить конъюнкцией. Т.е. согласно таблице истинности пункта 1 получим, что СКНФ данной функции примет вид

Построим полином Жегалкина.

Для построения полинома Жегалкина воспользуемся СДНФ заданной булевой функции, заменив операцию дизъюнкции () на операцию строгой дизъюнкции (). Затем заменяем выражения на . Далее раскрываем скобки и упрощаем по правилу .

По заданной матрице смежности построить неориентированный граф, составить таблицу степеней вершин, матрицу инцидентности, таблицу расстояний и условных радиусов, найти радиус и центр графа.

║ 0 0 0 1 0 1 0 1 0 ║

║ 0 0 0 0 1 0 1 0 1 ║

║ 0 0 0 0 0 0 1 0 0 ║

║ 1 0 0 0 1 0 0 1 0 ║

A(G) = ║ 0 1 0 1 0 1 0 0 0 ║

║ 1 0 0 0 1 0 1 0 0 ║

║ 0 1 1 0 0 1 0 0 1 ║

║ 1 0 0 1 0 0 0 0 0 ║

║ 0 1 0 0 0 0 1 0 0 ║

Выяснить, применима ли машина Тьюринга T к слову P. Если применима, то выписать результат T(P) применения машины Тьюринга T к слову P.

Найти число способов расстановки 31 томов на книжной полке, при котором первые 30 томов стоят рядом в порядке возрастания номеров

В военном подразделении служат 11 офицеров и 13 рядовых оперативная группа состоит из командира, заместителя и 10 рядовых, причём командир и заместитель назначаются случайным образом из числа офицеров. Найти число возможных различных оперативных групп.

Найти множество всех подмножеств множества

Найти декартово произведение множеств A=, B=

В вузе 23 отличников, 64 хорошистов и 492 троечников. Делегация на студенческую конференцию включает 9 отличников, 7 хорошистов и 5 троечников. Найти число возможных делегаций.

Даны числовые множества

Найти множество A&(BC).

На множестве M= задано отношение

Выяснить, является ли это отношение отношением эквивалентности, отношением частичного порядка, отношением строгого порядка или отношением линейного порядка.