В задании 23 из второй части диагностической работы для 9 класса по математике, прошедшей в московских школах 19 декабря 2011, была предложена геометрическая задача. Для ее решения от учеников требовалось знание так называемой теоремы о секущей и касательной, о существовании которой многие девятиклассники, как оказалось, и не подозревали. Выявив сей пробел, постараемся тут же его закрыть.
Лемма о вневписанном угле: величина угла, образованного касательной и хордой, имеющими общую точку на окружности, равна половине угловой величины дуги, заключенной между его сторонами.
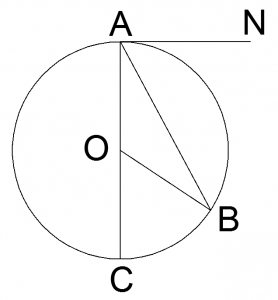
Например, на рисунке ∠BAN = 1/2 AB. Докажем это. Проведем диаметр АС. Касательная перпендикулярна диаметру, проведенному в точке касания, следовательно, ∠CAN = 90°. Известно, что вписанный угол равен половине центрального угла дуги, на которую он опирается. Тогда ∠BAC = ∠BOC/2, ∠NAB = 90° — ∠BAC, значит ∠NAB = 90° — ∠BOC/2 = (180° — ∠BOC)/2 = ∠АОВ/2, то есть равен половине угловой величины дуги ВА.
Теорема о секущей и касательной: если из внешней точки к окружности проведены касательная и секущая, то квадрат отрезка касательной от данной точки до точки касания равен произведению длин отрезков секущей от данной точки до точек её пересечения с окружностью.
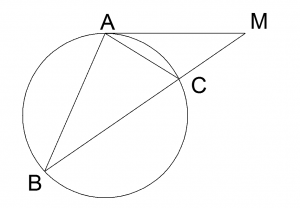
Например, на рисунке МА 2 = МВ · МС. Доказать это несложно. Действительно, вневписанный угол CAM равен вписанному углу ABC, поскольку оба опираются на одну дугу. Тогда треугольники АМС и ВМА подобны по двум углам (∠CAM = ∠ABC, ∠M — общий). Из подобия следует, что MC : MA = МА : MB, откуда получаем, что МА 2 = МВ · МС.
На этом теоретическая часть закончена, перейдем к практике. Разберем одно из заданий диагностической работы по математике для 9 класса, прошедшей в Москве 19 декабря 2011 года.
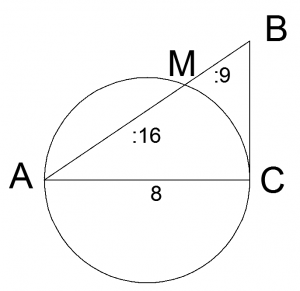
Пример. Длина катета AC прямоугольного треугольника ABC равна 8 см. Окружность с диаметром AC пересекает гипотенузу AB в точке M. Найдите площадь треугольника ABC, если известно, что AM : MB = 16 : 9.
Решение:
Пусть BC = y см, AM = 16x см и MB = 9x см. Поэтому гипотенуза AB = 25x см.
По теореме Пифагора: y 2 = 625x 2 — 64.
По теореме о секущей и касательной: y 2 =25x · 9x = 225x 2 .
Следовательно, 225x 2 = 625x 2 — 64, откуда x 2 = 4/25.
Тогда y 2 = 225 · 4/25; y = 15 · 2/5 = 6.
Следовательно, искомая площадь треугольника равна:
1/2 · AC · BC = 1/2 · 8 · 6 = 24 см 2 .
Видео:Длина катета прямоугольного треугольника равна 8 см. Окружность с диаметром пересекает гипотенузуСкачать

Окружность с диаметром ас пересекает гипотенузу ав прямоугольного треугольника
БАЗА ЗАДАНИЙ
Задание № 16. Планиметрия с доказательством.
1. Прямая, проходящая через вершину B прямоугольника ABCD перпендикулярно диагонали AC, пересекает сторону AD в точке M, равноудалённой от вершин B и D.
а) Докажите, что ∠ABM =∠DBС = 30°.
б) Найдите расстояние от центра прямоугольника до прямой CM, если BC = 9.
2. К окружности, вписанной в квадрат ABCD, проведена касательная, пересекающая стороны AB и AD в точках M и N соответственно.
а) Докажите, что периметр треугольника AMN равен стороне квадрата.
б) Прямая MN пересекает прямую CD в точке P. В каком отношении делит сторону BC прямая, проходящая через точку P и центр окружности, если AM : MB = 1 : 3?
Ответ: б) 1:3
3. Диагонали AC и BD четырёхугольника ABCD, вписанного в окружность, пересекаются в точке P, причём BC=CD.
а) Докажите, что AB:BC = AP:PD.
б) Найдите площадь треугольника COD, где O— центр окружности, вписанной в треугольник ABD, если дополнительно известно, что BD — диаметр описанной около четырёхугольника ABCD окружности, AB = 6, а BC = 6√2.
Ответ: б) 18√3
4. В треугольнике ABC точки A 1 , B 1 , C 1 — середины сторон BC, AC и A B соответственно, AH— высота, ∠BAC = 60°, ∠BCA = 45°.
а) Докажите, что точки A1, B1, C1, H— лежат на одной окружности.
б) Найдите A1 H, если BC = 2√3.
5. Две окружности касаются внутренним образом в точке A, причём меньшая проходит через центр большей. Хорда BC большей окружности касается меньшей в точке P. Хорды AB и AC пересекают меньшую окружность в точках K и M соответственно.
а) Докажите, что прямые KM и BC параллельны.
б) Пусть L— точка пересечения отрезков KM и AP. Найдите AL, если радиус большей окружности равен 10, а BC = 16.
Ответ: б) √10
6. Две окружности касаются внутренним образом в точке A, причём меньшая окружность проходит через центр O большей. Диаметр BC большей окружности вторично пересекает меньшую окружность в точке M, отличной от A. Лучи AO и AM вторично пересекают большую окружность в точках P и Q соответственно. Точка C лежит на дуге AQ большей окружности, не содержащей точку P.
а) Докажите, что прямые PQ и BC параллельны.
б) Известно, что sin ∠AOC=√15/4. Прямые PC и AQ пересекаются в точке K. Найдите отношение QK:KA.
Ответ: б) 1:4
7. Две окружности касаются внутренним образом в точке K, причём меньшая проходит через центр большей. Хорда MN большей окружности касается меньшей в точке C. Хорды KM и KN пересекают меньшую окружность в точках A и B соответственно, а отрезки KC и AB пересекаются в точке L.
а) Докажите, что CN:CM = LB:LA.
б) Найдите MN, если LB:LA = 2:3, а радиус малой окружности равен √23.
Ответ: б) 115/6
8. Дан прямоугольный треугольник ABC с прямым углом C. На катете AC взята точка M. Окружность с центром O и диаметром CM касается гипотенузы в точке N.
а) Докажите, что прямые MN и BO параллельны.
б) Найдите площадь четырёхугольника BOMN, если CN = 4 и AM:MC = 1:3.
9. Точка B лежит на отрезке AC. Прямая, проходящая через точку A, касается окружности с диаметром BC в точке M и второй раз пересекает окружность с диаметром AB в точке K. Продолжение отрезка MB пересекает окружность с диаметром AB в точке D.
а) Докажите, что прямые AD и MC параллельны.
б) Найдите площадь треугольника DBC, если AK = 3 и MK = 12.
10. Точка M лежит на стороне BC выпуклого четырёхугольника ABCD, причём B и C — вершины равнобедренных треугольников с основаниями AM и DM соответственно, а прямые AM и MD перпендикулярны.
а) Докажите, что биссектрисы углов при вершинах B и C четырёхугольника ABCD пересекаются на стороне AD.
б) Пусть N— точка пересечения этих биссектрис. Найдите площадь четырёхугольника ABCD, если известно, что BM:MC=1:3, а площадь четырёхугольника, стороны которого лежат на прямых AM, DM, BN и CN, равна 18.
11. В равнобедренном тупоугольном треугольнике ABC на продолжение боковой стороны BC опущена высота AH. Из точки H на сторону AB и основание AC опущены перпендикуляры HK и HM соответственно.
а) Докажите, что отрезки AM и MK равны.
б) Найдите MK, если AB = 5, AC = 8.
Ответ: б) 2,88
12. Точка O — центр окружности, описанной около остроугольного треугольника ABC, I — центр вписанной в него окружности, H — точка пересечения высот. Известно, что ∠BAC = ∠OBC+∠OCB.
а) Докажите, что точка H лежит на окружности, описанной около треугольника BOC.
б) Найдите угол OHI, если ∠ABC = 55°.
13. Точки P, Q, W делят стороны выпуклого четырёхугольника ABCD в отношении AP:PB = CQ:QB = CW:WD = 3:4, радиус окружности, описанной около треугольника PQW, равен 10, PQ = 16, QW = 12, угол PWQ— острый.
а) Докажите, что треугольник PQW— прямоугольный.
б) Найдите площадь четырёхугольника ABCD.
14. Окружность проходит через вершины В и С треугольника АВС и пересекает АВ и АС в точках C 1 , B 1 соответственно.
а) Докажите, что треугольник АВC подобен треугольнику AB 1 C 1 .
б) Вычислите длину стороны ВС и радиус данной окружности, если ∠ А = 45°, B 1 C 1 =6 и площадь треугольника AB 1 C 1 в восемь раз меньше площади четырёхугольника BCB 1 C 1 .
15. Дана трапеция ABCD с основаниями AD и BC. Диагональ BD разбивает её на два равнобедренных треугольника с основаниями AD и CD.
а) Докажите, что луч AC— биссектриса угла BAD.
б) Найдите CD, если известны диагонали трапеции: AC = 15 и BD = 8,5.
16. В прямоугольном треугольнике АВС с прямым углом С точки М и N – середины катетов АС и ВС соответственно, СН – высота.
а) Докажите, что прямые MH и NH перпендикулярны
б) Пусть Р – точка пересечения прямых АС и NH, а Q – точка пересечения прямых ВС и MH. Найдите площадь треугольника PQM, если АН = 12 и ВН = 3.
17. В треугольнике АВС угол АВС равен 60°. Окружность, вписанная в треугольник, касается стороны AC в точке M.
а) Докажите, что отрезок BM не больше утроенного радиуса вписанной в треугольник окружности.
б) Найдите sin ∠BMC если известно, что отрезок ВМ в 2,5 раза больше радиуса вписанной в треугольник окружности.
Ответ: б) 0,65
18. В треугольнике АВС проведены высоты АК и СМ. На них из точек М и К опущены перпендикуляры МЕ и КН соответственно.
а) Докажите, что прямые ЕН и АС параллельны.
б) Найдите отношение ЕН:АС, если угол АВС равен 30.
Ответ: б) 3:4
19. Окружность, вписанная в треугольник KLM, касается сторон KL, LM, MK в точках A, B и C соответственно.
а) Докажите, что KC = (KL+KM-LM)/2 .
б) Найдите отношение LB:BM, если известно, что KC:CM = 3:2 и ∠ MKL = 60.
Ответ: б) 5:2
20. Дана равнобедренная трапеция ABCD с основаниями AD и BC. Окружность с центром O, построенная на боковой стороне AB как на диаметре, касается боковой стороны CD и второй раз пересекает большее основание AD в точке H, точка Q — середина CD.
а) Докажите, что четырёхугольник DQOH — параллелограмм.
б) Найдите AD, если ∠BAD = 75° и BC =1.
Ответ: б) 3
21. Квадрат ABCD вписан в окружность. Хорда CE пересекает его диагональ BD в точке K.
а) Докажите, что CK*CE = AB*CD.
б) Найдите отношение CK к KE, если ∠ ECD = 15.
Ответ: б) 2:1
22. В прямоугольном треугольнике ABC точки M и N – середины гипотенузы AB и катета BC соответственно. Биссектриса ∠ BAC пересекает прямую MN в точке L
а) Докажите, что треугольники AML и BLC подобны.
б) Найдите отношение площадей этих треугольников, если cos ∠BAC = 7/25.
Ответ: б) 25:36
23. Окружность касается стороны AC остроугольного треугольника ABC и делит каждую из сторон AB и BC на три равные части.
а) Докажите, что треугольник ABC равнобедренный.
б) Найдите, в каком отношении высота этого треугольника делит сторону BC.
Ответ: б) 5:4
24. На катетах AC и BC прямоугольного треугольника ABC как на диаметрах построены окружности, второй раз пересекающиеся в точке M. Точка Q лежит на меньшей дуге MB окружности с диаметром BC. Прямая CQ второй раз пересекает окружность с диаметром AC в точке P.
а) Докажите, что прямые PM и QM перпендикулярны.
б) Найдите PQ, если AM = 1, BM = 3, а Q – середина дуги MB.
25. Окружность, построенная на медиане BM равнобедренного треугольника ABC как на диаметре, второй раз пересекает основание BC в точке K.
а) Докажите, что отрезок BK втрое больше отрезка CK.
б) Пусть указанная окружность пересекает сторону AB в точке N. Найдите AB, если BK = 24 и BN = 23.
26. В прямоугольной трапеции ABCD с прямым углом при вершине A расположены две окружности. Одна из них касается боковых сторон и большего основания AD, вторая – боковых сторон, меньшего основания BC и первой окружности.
а) Прямая, проходящая через центр окружностей, пересекает основание AD в точке P. Докажите, что AP/PD = sin ∠D.
б) Найдите площадь трапеции, если радиусы окружностей равны 3 и 1.
27. В трапецию ABCD с основаниями AD и BC вписана окружность с центром O.
а) Докажите, что sin ∠AOD = sin ∠ BOS.
б) Найдите площадь трапеции, если ∠ BAD = 90, а основания равны 5 и 7.
28. Дана трапеция с диагоналями равными 8 и 15. Сумма оснований равна 17.
а) Докажите, что диагонали перпендикулярны.
б) Найдите площадь трапеции.
Видео:7 кл г. Теорема: «катет лежавший напротив угла в 30 градусов равен половине гипотенузы»Скачать

Задача 16 геометрия на ЕГЭ-2021 по математике
На этой странице — обзор разных типов заданий № 16 ЕГЭ-2021 по математике, то есть задач по геометрии.
Все они имеют нечто общее: во-первых, это стандартный уровень сложности, то есть вполне решаемые задачи. Пункт (а) в них вообще простой.
Во-вторых, в каждой из них применяются свойства четырехугольников, вписанных в окружности.
В первой задаче такая окружность находится почти сразу, причем она – вспомогательная, и ее можно даже не изображать на чертеже. Главное – найти равные вписанные углы, опирающиеся на равные дуги или на одну дугу.
Также здесь использована формула синуса тройного угла. Если вы ее забыли – не беда. Ведь а формулу синуса суммы вы знаете.
1. Дана равнобедренная трапеция ABCD, в которой меньшее основание ВС равно боковой стороне. Точка Е такова, что ВЕ перпендикулярно AD и СЕ перпендикулярно BD.
а) Доказать, что угол АЕВ равен углу BDA.
б) Найти площадь трапеции ABCD, если АВ = 32, косинус угла АDВ равен
– равнобедренный, CM – высота, проведенная к основанию, значит, M – середина BD.
Докажем, что точки A, B, C, D, E лежат на одной окружности.
ABCD – равнобедренная трапеция, ее можно вписать в окружность.
В – медиана и высота, значит, равнобедренный, BE = ED.
Тогда по трем сторонам, четырехугольник BCDE можно вписать в окружность, т.к.
Так как вокруг можно описать только одну окружность и вокруг четырехугольников ABCD и BCDE тоже можно описать окружность, точки A, B, C, D, E лежат на одной окружности, так как опираются на одну и ту же дугу AB (точки E и D лежат по одну сторону от прямой AD).
б) Так как AB = BC = CD, то дуги AB, BC и CD также равны.
Четырехугольник ABDE вписан в окружность, тогда
По формуле синуса тройного угла,
тогда по теореме синусов
Проведем в трапеции ABCD высоту CK, тогда
BH и CK – высоты трапеции, а так как трапеция равнобедренная, то
Во второй задаче мы увидим ту же идею: вспомогательную окружность. Это один из методов, помогающих решать задачи ЕГЭ по геометрии. Есть здесь и другой мощный прием – использование двух пар подобных треугольников. И еще свойство высоты прямоугольного треугольника, проведенной к гипотенузе. Если вы в восьмом и девятом классе учили геометрию – вы должны владеть этими приемами.
2. Дан прямоугольный треугольник АВС с прямым углом С. Из вершины С на гипотенузу опущена высота СН, на АС и ВС соответственно отмечены точки М и N так, что угол MHN – прямой.
а) Докажите, что треугольники МNH и АВС подобны.
б) Найдите СN, если АС = 5, СМ = 2, ВС = 3.
а) Рассмотрим четырехугольник CMHN.
по условию, значит, CMHN можно вписать в окружность; вписанные, опираются на дугу HN.
Запишем соотношение сходственных сторон.
По условию, AM = 3, найдем CH — высоту
по теореме Пифагора,
AH — проекция катета AC на гипотенузу, по свойствам прямоугольного треугольника, отсюда
В следующей задаче мы снова видим окружность и вписанную в нее трапецию. И наверное, вы уже заметили: пункт (а) задач по геометрии на ЕГЭ часто оказывается подсказкой для решения пункта (б). То, что мы доказали в (а), мы используем в пункте (б).
3. Даны 5 точек на окружности: A, B, C, D, E, причем АЕ = ED = CD, ВЕ перпендикулярен АС.
Точка Т – точка пересечения АС и BD.
а) Докажите, что отрезок ЕС делит отрезок ТD пополам.
б) Найдите площадь треугольника АВТ, если BD = 10, АЕ =
Докажем, что M — середина TD.
Если AE = ED = DC, то дуги AE, ED, DC, также равны;
— накрест лежащие, при пересечении AC и DE секущей CE, значит, AEDC — равнобедренная трапеция. значит, BD — диаметр окружности.
(опирается на диаметр), по катету и гипотенузе, тогда DM — биссектриса равнобедренного т.к. — равнобедренный, то DM — медиана M — середина CE, кроме того, DM — высота
В — медиана и высота, значит, — равнобедренный, а так как — накрест лежащие, при параллельных прямых AC и DE и секущей CE, то по боковой стороне и углу при основании, тогда
CDET — ромб, M — точка пересечения его диагоналей, M — середина TD.
Мы нашли, что AE = ED = CD = CT = ET.
BD = 10 — диаметр окружности.
— равнобедренный, AE = ET, — высота и медиана
Тогда BN — медиана и высота — равнобедренный, AB = BT.
Обозначим тогда — опираются на дугу AE,
Из по теореме синусов:
И еще одна трапеция, вписанная в окружность. Теперь вы точно выучите ее свойства наизусть! Также здесь применяется теорема о пересекающихся хордах. Все эти полезные теоремы, свойства и признаки можно найти в нашей универсальной шпаргалке – Справочнике Анны Малковой для подготовки к ЕГЭ по математике. Скачать Справочник бесплатно можно здесь.
4. Трапеция с большим основанием AD и высотой ВН вписана в окружность. Прямая BH пересекает окружность в точке К.
б) Найдите AD, если: радиус окружности равен шести, СК пересекается с AD в точке N и площадь четырехугольника BHNC в 24 раза больше, чем плошать треугольника KHN.

а) Трапеция ABCD вписана в окружность, следовательно, AB = CD (трапеция равнобокая)
Тогда — вписанные, опираются одну и ту же на дугу AK;
следовательно, CK — диаметр окружности, так как вписанный угол, опирающийся на диаметр, прямой; — опирается на диаметр CK, значит,
(опираются на дугу BC), тогда
Обозначим так как HE = BC,
Из подобия треугольников KNH и KCB следует, что тогда
По теореме о пересекающихся хордах,
Представив левую часть уравнения как разность квадратов, получим:
По смыслу задачи тогда и значит
Задача по геометрии на ЕГЭ по математике оценивается в 3 балла. Как видите, в 2021 году эти 3 балла за геометрию можно было получить без особенных трудностей. На нашем Онлайн-курсе подготовки к ЕГЭ мы решаем и такие задачи по геометрии, и более сложные. Если ты сейчас в 10-м или в 11-м классе – попробуй бесплатно Демо-доступ к Онлайн-курсу.
5. (Резервный день) Окружность с центром О, построенная на катете АС прямоугольного треугольника АВС, как на диаметре, пересекает гипотенузу АВ в точках А и D. Касательная, проведенная к этой окружности в точке D, пересекает катет ВС в точке М.
А) Докажите, что ВМ = СМ
Б) Прямая DM пересекает прямую АС в точке Р, прямая ОМ пересекает прямую ВР в точке К.
Найдите ВК : КР, если
а) Так как – радиус окружности, – равнобедренный, так как (касательная перпендикулярна радиусу, проведенному в точку касания), тогда
– угол между касательной и хордой,
Тогда т.е. – высота – прямоугольный, – равнобедренный, отсюда
Найдем BK : KP, если тогда
Значит, (вертикальные), — равнобедренный, тогда так как MK – биссектриса
📽️ Видео
ЕГЭ Задание 16 Теорема косинусовСкачать

Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Диаметр АВ окружности радиуса R. Окружность, диаметр, хорда и прямоугольный треугольник в задаче...Скачать

Всё про углы в окружности. Геометрия | МатематикаСкачать

17 задание ЕГЭ математика профильСкачать

7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать

ОГЭ. Задание 24. Геометрическая задача на вычислениеСкачать

Задача по геометрии на прямоугольный треугольник и теорему Пифагора из реального ОГЭ по математикеСкачать

Задание 25 (В1) ОГЭ по математике ▶ №20 (Минутка ОГЭ)Скачать

ОГЭ. Задание 24. Геометрическая задача на вычисление.Скачать

№705. Около прямоугольного треугольника ABC с прямым углом С описана окружность. Найдите радиусСкачать

Задания 23,24. Тест 17. ОГЭ. Математика.Скачать

Геометрия 8 класс за 1 час | Математика | УмскулСкачать

№704. Окружность с центром О описана около прямоугольного треугольника, а) ДокажитеСкачать

ОГЭ без рекламы математика вариант 9 и 10 задача 25Скачать

ОГЭ. Задание 24. Геометрическая задача на вычисление.Скачать

8 класс, 39 урок, Описанная окружностьСкачать

№702. В окружность вписан треугольник ABC так, что АВ — диаметр окружности. Найдите углыСкачать