Диагонали АС и ВD выпуклого четырёхугольника ABCD пересекаются в точке Р. Известно, что угол DAC равен 90°, а в 2 раза больше угла ADB. Сумма угла DBС и удвоенного угла ADС равна 180°.
а) Докажите, что ВР = 2AP.
б) Найдите площадь четырёхугольника AВCD, если BD = 8 и точка Р является серединой диагонали BD.
а) Пусть биссектриса угла РСВ пересекает отрезок РВ в точке М. Обозначим буквой β угол ADB. Получаем, что
Так как 
по свойству вертикальных углов, треугольники APD и МРС подобны, поэтому ∠PMC = 90°. Таким образом, в треугольнике ВСР биссектриса СМ является высотой, а значит, треугольник ВСР равнобедренный и PM = MB, CP = CB.
В треугольнике DBC:
Из этого равенства и из того, что 
следует, что ∠PCD = ∠PDC. Поэтому треугольник PCD равнобедренный и PD = PC. Значит, треугольники APD и МРС равны, поэтому 
откуда следует, что BP = 2AP.
б) Точка Р является серединой отрезка BD, поэтому 
Отсюда следует, что треугольник ВСР равносторонний, поэтому ∠BPC = 60°. Из равенства 
получаем, что AP = 2 и 
Теперь найдём площадь четырёхугольника AВCD:
Ответ: б) 
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Имеется верное доказательство утверждения пункта a) и обоснованно получен верный ответ в пункте б) | 3 |
| Получен обоснованный ответ в пункте б) имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | 2 |
| Имеется верное доказательство утверждения пункта а) при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, Содержание Видео:№382. Диагонали параллелограмма ABCD пересекаются в точке О. Докажите, что четырехугольникСкачать  Диагонали четырехугольника abcd пересекаются в точке p докажите что произведение площадейЗадание 16. Диагонали АС и BD четырёхугольника ABCD, вписанного в окружность, пересекаются в точке P, причём BC = CD. а) Докажите, что AB:BC=AP:PD. б) Найдите площадь треугольника COD, где О — центр окружности, вписанной в треугольник ABD, если дополнительно известно, что BD — диаметр описанной около четырёхугольника ABCD окружности, АВ = 5, а ВС = 5√2. а) Так как стороны BC=CD, то и дуга BC равна дуге CD. На эти дуги опираются равные углы: BAC, CAD, CBD, CDB. Получаем подобные треугольники BPC и APD (по двум углам), следовательно, Далее, треугольники BPC и ABC также подобны по двум углам, поэтому В результате из (1) и (2), имеем: б) Так как BD – диаметр окружности, то треугольники BCD и ABD – прямоугольные с прямыми углами C и A соответственно. Также по условию задания BC=CD=5√2, получаем Рассмотрим прямоугольный треугольник BAD, в котором AB=5, BD=10, следовательно, угол BDA=30°, а угол ODO1 = 15° (так как O – центр вписанной окружности, поэтому DO – биссектриса). Далее, из равнобедренного треугольника BCD с основание BD получаем, что угол CDB=45°, следовательно, угол ODC=45+15=60°. Из прямоугольного треугольника ABD и полупериметр треугольника ABD, равен: Найдем отрезок DE=p-AB (как отрезок части касательной), имеем: и радиус вписанной окружности: Рассмотрим прямоугольный треугольник OED, из которого Рассмотрим треугольник OCD, в котором Ответ: Видео:25)В трапеции ABCD с основаниями AD и BC диагонали пересекаются в точке O. Докажите, что площади треСкачать  Диагонали четырехугольника abcd пересекаются в точке p докажите что произведение площадейдЙБЗПОБМЙ ЧЩРХЛМПЗП ЮЕФЩТЈИХЗПМШОЙЛБ ABCD РЕТЕУЕЛБАФУС Ч ФПЮЛЕ E . йЪЧЕУФОП, ЮФП РМПЭБДШ ЛБЦДПЗП ЙЪ ФТЕХЗПМШОЙЛПЧ ABE Й DCE ТБЧОБ 1, РМПЭБДШ ЧУЕЗП ЮЕФЩТЈИХЗПМШОЙЛБ ОЕ РТЕЧПУИПДЙФ 4, AD = 3. оБКДЙФЕ УФПТПОХ BC . рПДУЛБЪЛБдПЛБЦЙФЕ, ЮФП BC || AD . тЕЫЕОЙЕфТЕХЗПМШОЙЛЙ ABD Й ACD ТБЧОПЧЕМЙЛЙ, ФБЛ ЛБЛ фПЗДБ ЙИ ЧЩУПФЩ, ПРХЭЕООЩЕ ОБ ПВЭЕЕ ПУОПЧБОЙЕ AD , ТБЧОЩ. уМЕДПЧБФЕМШОП, BC || AD . рХУФШ BC = x . йЪ РПДПВЙС ФТЕХЗПМШОЙЛПЧ BEC Й DEA УМЕДХЕФ, ЮФП рП ХУМПЧЙА ЪБДБЮЙ S ABCD у ДТХЗПК УФПТПОЩ, УХННБ ДЧХИ ЧЪБЙНОП ПВТБФОЩИ РПМПЦЙФЕМШОЩИ ЮЙУЕМ ОЕ НЕОШЫЕ 2, РТЙЮЈН ТБЧЕОУФЧП ДПУФЙЗБЕФУС ФПЗДБ Й ФПМШЛП ФПЗДБ, ЛПЗДБ ЛБЦДПЕ ЙЪ ЬФЙИ ЮЙУЕМ ТБЧОП 1. фТЕХЗПМШОЙЛЙ ABD Й ACD ТБЧОПЧЕМЙЛЙ, ФБЛ ЛБЛ фПЗДБ ЙИ ЧЩУПФЩ, ПРХЭЕООЩЕ ОБ ПВЭЕЕ ПУОПЧБОЙЕ AD , ТБЧОЩ. уМЕДПЧБФЕМШОП, BC || AD . рХУФШ BC = x . йЪ РПДПВЙС ФТЕХЗПМШОЙЛПЧ BEC Й DEA УМЕДХЕФ, ЮФП рП ХУМПЧЙА ЪБДБЮЙ S ABCD у ДТХЗПК УФПТПОЩ, УХННБ ДЧХИ ЧЪБЙНОП ПВТБФОЩИ РПМПЦЙФЕМШОЩИ ЮЙУЕМ ОЕ НЕОШЫЕ 2, РТЙЮЈН ТБЧЕОУФЧП ДПУФЙЗБЕФУС ФПЗДБ Й ФПМШЛП ФПЗДБ, ЛПЗДБ ЛБЦДПЕ ЙЪ ЬФЙИ ЮЙУЕМ ТБЧОП 1. фТЕХЗПМШОЙЛЙ ABD Й ACD ТБЧОПЧЕМЙЛЙ, ФБЛ ЛБЛ фПЗДБ ЙИ ЧЩУПФЩ, ПРХЭЕООЩЕ ОБ ПВЭЕЕ ПУОПЧБОЙЕ AD , ТБЧОЩ. уМЕДПЧБФЕМШОП, BC || AD . рХУФШ BC = x . йЪ РПДПВЙС ФТЕХЗПМШОЙЛПЧ BEC Й DEA УМЕДХЕФ, ЮФП рП ХУМПЧЙА ЪБДБЮЙ S ABCD у ДТХЗПК УФПТПОЩ, УХННБ ДЧХИ ЧЪБЙНОП ПВТБФОЩИ РПМПЦЙФЕМШОЩИ ЮЙУЕМ ОЕ НЕОШЫЕ 2, РТЙЮЈН ТБЧЕОУФЧП ДПУФЙЗБЕФУС ФПЗДБ Й ФПМШЛП ФПЗДБ, ЛПЗДБ ЛБЦДПЕ ЙЪ ЬФЙИ ЮЙУЕМ ТБЧОП 1. 🌟 ВидеоГеометрия В трапеции ABCD с основаниями AD и BC диагонали пересекаются в точке P. Докажите, чтоСкачать  Геометрия Диагонали четырехугольника ABCD пересекаются в точке O Известно что угол A = углу D AO=ODСкачать  №478. В выпуклом четырехугольнике диагонали взаимно перпендикулярны. Докажите, что площадьСкачать 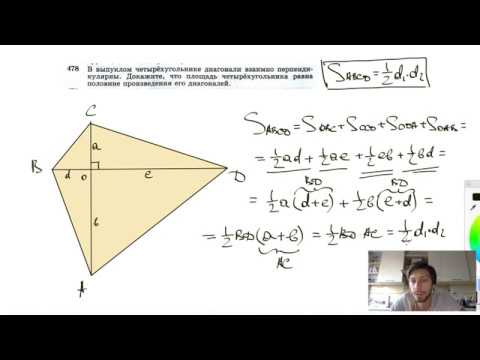 Геометрия Диагонали AC и BD трапеции ABCD пересекаются в точке O. Площади треугольников AOD и BOCСкачать  №402. Диагонали прямоугольника ABCD пересекаются в точке О. Докажите, что треугольникиСкачать  1.36.1. Планиметрия. Гордин Р.К.Скачать  №43. Диагонали четырёхугольника ABCD пересекаются в точке M. Известно, что углы BAC и ADC прямыеСкачать  №511. В трапеции ABCD с боковыми сторонами АВ и CD диагонали пересекаются в точке О. а) Сравните плоСкачать 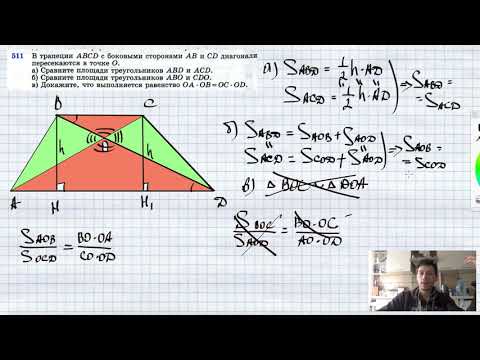 №521. Докажите, что если диагонали четырехугольника ABCD взаимно перпендикулярны, то AD2 +ВС2 =AB2+CСкачать  Задания 23,24. Тест 21. ОГЭ. Математика.Скачать  Все про ПАРАЛЛЕЛОГРАММ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // ГеометрияСкачать  Все про РОМБ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // Геометрия 8 классСкачать  ОГЭ Задание 25 Свойства площадейСкачать 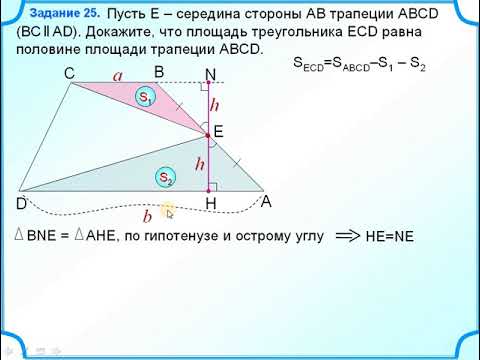 №403. В прямоугольнике ABCD диагонали пересекаются в точке О. Найдите периметрСкачать  #26. EGMO-2022, Problem 6Скачать  Задача на доказательство из 2-ой части ОГЭ по математике? Легко!Скачать  №552. Диагонали трапеции ABCD с основаниями АВ и CD пересекаются в точке О. Найдите:Скачать  Доказать,что площадь треугольника KAB равна половине площади трапецииСкачать  |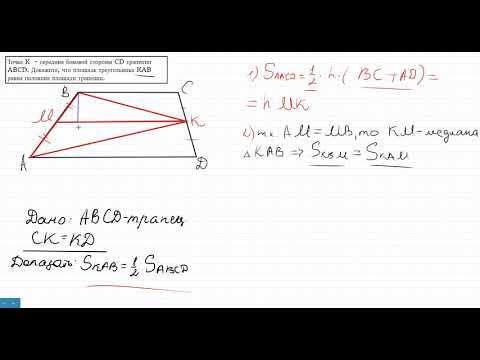
и
или 
(1)
или 
(2)
, следовательно, треугольник ODC – равносторонний. Площадь этого треугольника, равна:
4, РПЬФПНХ
4, РПЬФПНХ
4, РПЬФПНХ