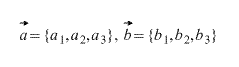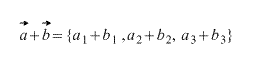Как сложить два вектора зная их длины

Сложение векторов. Векторная сумма. Правила сложения векторов. Геометрическая сумма. Он-лайн калькулятор

В механике существуют два типа величин:

• скалярные величины, задающие некоторое числовое значение — время, температура, масса и т.д.
• векторные величины, которые вместе с некоторым числовым значением задают направление — скорость, сила и т.д..

Рассмотрим сначала алгебраический подход к сложению векторов.

Покоординатное сложение векторов.

Тогда координаты вектора, получившегося при сложении этих двух векторов вычисляются по формуле:

В двумерном случае все абсолютно анологично, просто отбрасываем третью координату.

Теперь перейдем к геометрическому смыслу сложения двух векторов:

При сложении векторов нужно учитывать и их числовые значения, и направления. Есть несколько широко используемых методов сложения:

• правило параллелограмма
• правило треугольника
• тригонометрический способ

Правило параллелограмма. Сложение векторов по правилу параллелограмма.

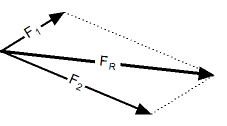Процедура сложения векторов по правилу параллелограмма заключается в следующем: нарисовать первый вектор, учитывая его величину и направление от начала первого вектора нарисовать второй вектор, также используя и его величину, и его направление дополнить рисунок до параллелограмма, считая, что два нарисованных вектора — это его стороны результирующим вектором будет диагональ параллелограмма, причем его начало будет совпадать с началом первого (а, значит, и второго) вектора.

Правило треугольника. Сложение векторов по правилу треугольника.

	Сложение векторов по правилу треугольника заключается в следующем: нарисовать первый вектор, используя данные о его длине ( числовой величине) и направлении от конца первого вектора нарисовать второй вектор, также учитывая и его размер, и его направление результирующим вектором будет вектор, начало которого совпадает с началом первого вектора, а конец — с концом второго.

Тригонометрический способ. Сложение векторов тригонометрическим способом.

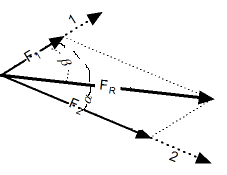Результирующий вектор сложения двух компланарных векторов может быть вычислен с помощью теоремы косинусов: Fрез. = [ F1 2 + F2 2 -2 F1 F2 cos(180 о -α) ] 1/2 (1) где F = числовое значение вектора α = угол между векторами 1 и 2 Угол между результирующим вектором и одним из исходных векторов может быть вычислен по теореме синусов: β = arcsin[ F2 *sin(180 o -α) / FR ] (2) где α = угол между исходными векторами

Пример — сложение векторов.

Сила 1 равна 5кН и воздействует на тело в направлении, на 80 o отличающемся от направления действия второй силы, равной 8 кН.

Результирующая сила вычисляется следующим образом:

F_рез = [ (5 кН) 2 + (8 кН) 2 — 2 (5 кН)(8 kН) cos(180 o — (80 o )) ] 1/2

Угол между результирующей силой и первой силой равен:

А угол между второй и результирующей силой можно посчитать следующим образом: as

α = arcsin [ (5 кН) sin(180 o — (80 o )) / (10,2 кН) ]

Он-лайн калькулятор сложения векторов.

Калькулятор ниже может быть использован для любвых векторных величин ( силы, скорости и т.д.) Точка начала вектора совпадает с началами обоих исходных векторов.

Консультации и техническая
поддержка сайта: Zavarka Team

Сложение векторов: длина суммы векторов и теорема косинусов

Определения скалярного произведения векторов через угол между ними

Сложение векторов по правилу треугольника (суммой векторов и называется вектор , начало которого совпадает с началом вектора , а конец — с концом вектора , при условии, что начало вектора приложено к концу вектора ) даёт возможность упрощать выражение перед вычислением произведений векторов.

Сложение векторов, заданных координатами (при сложении одноимённые координаты складываются) даёт возможность узнать, как расположен относительно начала координат вектор, являющийся суммой слагаемых векторов. Подробно эти две операции разбирались на уроке «Векторы и операции над векторами».

Теперь же нам предстоит узнать, как найти длину вектора, являющегося результатом сложения векторов. Для этого потребуется использовать теорему косинусов. Такую задачу приходится решать, например, когда дорога из пункта A в пункт С — не прямая, а отклоняется от прямой, чтобы пройти ещё через какой-то пункт B, а нужно узнать длину предполагаемой прямой дороги. Кстати, геодезия — одна из тех сфер деятельности, где тригонометрические функции применяются во всех их полноте.

При сложении векторов для нахождения длины суммы векторов используется теорема косинусов. Пусть и — векторы, — угол между ними, а — сумма векторов как результат сложения векторов по правилу треугольника. Тогда верно следующее соотношение:

,

где — угол, смежный с углом . У смежных углов одна сторона общая, а другие стороны лежат на одной прямой (см. рисунок выше).

Поэтому для сложения векторов и определения длины суммы векторов нужно извлечь квадратный корень из каждой части равенства, тогда получится формула длины:

.

В случае вычитания векторов () происходит сложение вектора с вектором , противоположным вектору , то есть имеющим ту же длину, но противоположным по направлению. Углы между и и и между и являются смежными углами, у них, как уже было отмечено, одна сторона общая, а другие стороны лежат на одной прямой. В случае вычитания векторов для нахождения длины разности векторов нужно знать следующее свойство косинусов смежных углов:

косинусы смежных углов равны по абсолютной величине (величине по модулю), но имеют противоположные знаки.

Перейдём к примерам.

Сложение векторов — решение примеров

Пример 1. Векторы и образуют угол . Их длины: и . Выполнить сложение векторов и найти их сумму . Выполнить вычитание векторов и найти их разность .

Решение. Из элементарной тригонометрии известно, что .

Шаг 1. Выполняем сложение векторов. Находим длину суммы векторов, поставляя в формулу длины косинус угла, смежного с углом между векторами:

Шаг 2. Выполняем вычитание векторов. Находим длину разности векторов, подставляя в формулу косинус «изначального» угла:

Выполнить сложение и вычитание векторов самостоятельно, а затем посмотреть решение

Пример 2. Векторы и образуют угол . Их длины: и . Выполнить сложение векторов и найти их сумму . Выполнить вычитание векторов и найти их разность .

Пример 3. Даны длины векторов и длина их суммы . Найти длину их разности .

Шаг 1. По теореме косинусов составляем уравнение, чтобы найти косинус угла, смежного с углом между векторами и находим его:

Не забываем, что косинус смежного угла получился со знаком минус. Это значит, что косинус «изначального» угла будет со знаком плюс.

Шаг 2. Выполняем вычитание векторов. Находим длину разности векторов, подставляя в формулу косинус «изначального» угла:

Пример 4. Даны длины векторов и длина их разности . Найти длину их суммы .

Шаг 1. По теореме косинусов составляем уравнение, чтобы найти косинус «изначального» угла (задача обратная по отношению к примеру 1) и находим его:

Шаг 2. Меняем знак косинуса и получаем косинус смежного угла между и :

Шаг 3. Выполняем сложение векторов. Находим длину суммы векторов, подставляя в формулу косинус смежного угла:

Пример 5. Векторы и взаимно перпендикулярны, а их длины . Найти длину их суммы и и длину их разности .

Два смежных угла, как нетрудно догадаться из приведённого в начале урока определения, в сумме составляют 180 градусов. Следовательно, смежный с прямым углом (90 градусов) угол — тоже прямой (тоже 90 градусов). Косинус такого угла равен нулю, то же самое относится и к косинусу смежного угла. Поэтому, подставляя это значение в выражения под корнем в формуле длины суммы и разности векторов, получаем нули как последние выражения — произведения под знаком корня. То есть длины суммы и разности данных векторов равны, вычисляем их:

Пример 6. Какому условию должны удовлетворять векторы и , чтобы имели место слелующие соотношения:

1) длина суммы векторов равна длине разности векторов, т. е. ,

2) длина суммы векторов больше длины разности векторов, т. е. ,

3) длина суммы векторов меньше длины разности векторов, т. е. ?

Находим условие для первого соотношения. Для этого решаем следующее уравнение:

То есть, для того, чтобы длина суммы векторов была равна длине их разности, необходимы, чтобы косинус угла между ними и косинус смежного ему угла были равны. Это условие выполняется, когда углы образуют прямой угол.

Находим условие для второго соотношения. Решаем уравнение:

Найденное условие выполняется, когда косинус угла между векторами меньше косинуса смежных углов. То есть, чтобы длина суммы векторов была больше длины разности векторов, необходимо, чтобы углы образовали острый угол (пример 1).

Находим условие для третьего соотношения. Решаем уравнение:

Найденное условие выполняется, когда косинус угла между векторами больше косинуса смежных углов. То есть, чтобы длина суммы векторов была меньше длины разности векторов, необходимо, чтобы углы образовали тупой угол.

Сложение и вычитание векторов

Формулы сложения и вычитания векторов

Формулы сложения и вычитания векторов для плоских задач

В случае плоской задачи сумму и разность векторов a = < a_x ; a_y > и b = < b_x ; b_y > можно найти, воспользовавшись следующими формулами:

Формулы сложения и вычитания векторов для пространчтвенных задач

В случае пространственной задачи сумму и разность векторов a = < a_x ; a_y ; a_z > и b = < b_x ; b_y ; b_z > можно найти, воспользовавшись следующими формулами:

Формулы сложения и вычитания n -мерных векторов

В случае n -мерного пространства сумму и разность векторов a = < a ₁ ; a ₂ ; . ; a_n > и b = < b ₁ ; b ₂ ; . ; b_n > можно найти, воспользовавшись следующими формулами:

Примеры задач на сложение и вычитание векторов

Примеры плоских задач на сложение и вычитание векторов

Примеры пространственных задач на сложение и вычитание векторов

Примеры задач на сложение и вычитание векторов с размерностью большей 3

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

🎦 Видео