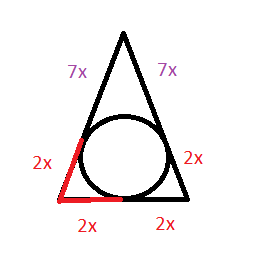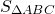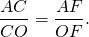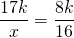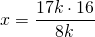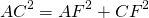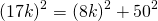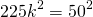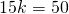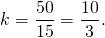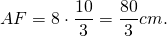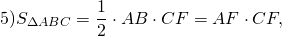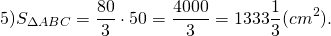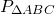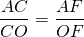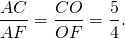Боковая сторона равнобедренного треугольника точкой касания вписанной окружности

Условие

боковая сторона равнобедренного треугольника делится точкой касания вписанной окружности в отношении 2 делить на 7 считая от вершины угла при основании треугольника найдите стороны треугольника если его периметр равен 110 см

Решение

Пусть в одной части х см.
Отношение 2:7 можно записать как 2х:7х.

По свойству касательной к окружности, проведенной из одной точки, отрезки касательных равны ( см. рисунок).

Поэтому боковые стороны имеют длину 2х+7х=9х
основание 2х+2х=4х
9х+9х+4х=110
22х=110
х=5
9*5=45 см -боковая сторона
4*5=20 см — основание

Почему основание ,2х+2х

По свойству касательной к окружности, проведенной из одной точки, отрезки касательных равны

Почему равняется 9х

7x черного цвета и 2х красного, всего 9х, треугольник равнобедренный. Одна боковая сторона 9х и вторая 9х, основание 2х+2х=4х

Видео:Задача 6 №27900 ЕГЭ по математике. Урок 128Скачать

Боковая сторона равнобедренного треугольника делится точкой касания вписанной окружности в отношении 2 : 7считая от вершины угла при основании треугольника найдите стороны треугольник если периметр ра?

Математика | 5 — 9 классы

Боковая сторона равнобедренного треугольника делится точкой касания вписанной окружности в отношении 2 : 7считая от вершины угла при основании треугольника найдите стороны треугольник если периметр равен 110.

Примем коэффициент пропорциональности отрезков, на которыебоковая сторона равнобедренного треугольника делится точкой касания вписанной окружности, за х, а основание — за у.

Тогда периметр треугольника равен 2 * (2х + 7х) + у = 110.

По свойству точки касания 2х = у / 2 или у = 4х (так как треугольник равнобедренный).

Подставим эту зависимость в первое уравнение.

Отсюда находим стороны треугольника : — боковые стороны равны 2 * 5 + 7 * 5 = 10 + 35 = 45, — основание равно 110 — 2 * 45 = 110 — 90 = 20.

Решение в приложении :

Видео:ЕГЭ Математика Задание 6#27935Скачать

Периметр равнобедреного треугольника равен 20 см?

Периметр равнобедреного треугольника равен 20 см.

Боковая сторона треугольника в 2 раза длиннее его основания .

Найдите длины основания и боковой стороны треугольника.

Видео:№691. Точка касания окружности, вписанной в равнобедренный треугольник, делит однуСкачать

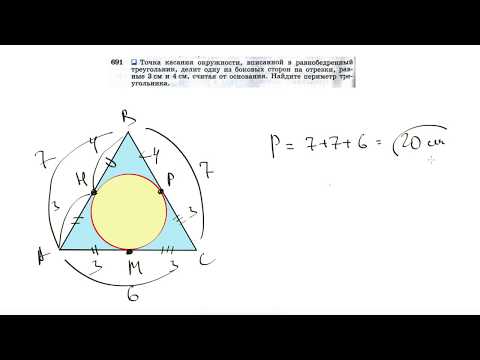
Периметр равнобедренного треугольника равен 35 см?

Периметр равнобедренного треугольника равен 35 см.

Основание равнобедренного треугольника в полтора раза длинее боковой стороны.

Найдите стороны треугольника.

Видео:ИТОГОВАЯ КОНТРОЛЬНАЯ РАБОТА по геометрии 7 классСкачать

Найдите периметр равнобедренного треугольника, боковая сторона которого точкой касания с вписанной в треугольник окружностью разделяется на отрезки 6 м и 8 м, если считать основания?

Найдите периметр равнобедренного треугольника, боковая сторона которого точкой касания с вписанной в треугольник окружностью разделяется на отрезки 6 м и 8 м, если считать основания.

Видео:Задача 6 №27934 ЕГЭ по математике. Урок 148Скачать

18. В равнобедренном треугольнике основание меньше боковой стороны на 4см?

18. В равнобедренном треугольнике основание меньше боковой стороны на 4см.

Найдите стороны треугольника, если его периметр равен 38 см.

19. В равнобедренном треугольнике основание в 2 раза больше боковой стороны треугольника, если его периметр равен 36 см.

20. В равнобедренном треугольнике основание в 3 раза меньше боковой стороны.

Найдите стороны треугольника, если егопериметр равен 56 см.

Видео:Геометрия Боковая сторона равнобедренного треугольника равна 18, основание равно 12. ВписаннаяСкачать

Основание равнобедренного треугольника в два раза короче боковой стороны, а периметр равен 75см?

Основание равнобедренного треугольника в два раза короче боковой стороны, а периметр равен 75см.

Найдите стороны треугольника.

Видео:Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторонСкачать

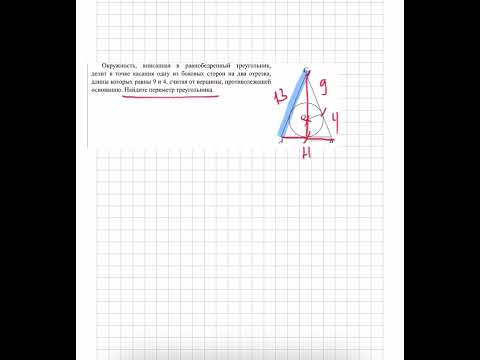
Точка касания окружности, вписанной в равнобедренный треугольник делит одну из боковых сторон на отрезки, равные 3см, 4см, считая от основания?

Точка касания окружности, вписанной в равнобедренный треугольник делит одну из боковых сторон на отрезки, равные 3см, 4см, считая от основания.

Найдите периметр треугольника.

Видео:Окружность вписана в равнобедренный треугольник. Найти её радиус.Скачать

Точка касания окружности, вписанной в равнобедренный треугольник делит одну из боковых сторон на отрезки, равные 3см, 4см, считая от основания?

Точка касания окружности, вписанной в равнобедренный треугольник делит одну из боковых сторон на отрезки, равные 3см, 4см, считая от основания.

Найдите периметр треугольника.

Видео:№487. Боковая сторона равнобедренного треугольника равна 17 см, а основание равно 16 смСкачать

Найдите боковую сторону равнобедренного треугольника, если центр вписанной в него окружности делит высоту, проведенную к основанию в отношении 7 : 5, считая от вершины, а основание равно 22 см?

Найдите боковую сторону равнобедренного треугольника, если центр вписанной в него окружности делит высоту, проведенную к основанию в отношении 7 : 5, считая от вершины, а основание равно 22 см.

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

В равнобедренном треугольнике основание равно 10см , а боковая сторона равна 13см ?

В равнобедренном треугольнике основание равно 10см , а боковая сторона равна 13см .

Найдите радиус окружности , вписанной в этот треугольник.

Видео:ЕГЭ 2017 | Задание 3 | Боковая сторона равнобедренного ... ✘ Школа ПифагораСкачать

В равнобедренном треугольнике высота проведённая к боковой стороне делит эту сторону на отрезке длиной 12 и 3 см считая от вершины треугольника противолежащей основанию Найдите площадь и периметр?

В равнобедренном треугольнике высота проведённая к боковой стороне делит эту сторону на отрезке длиной 12 и 3 см считая от вершины треугольника противолежащей основанию Найдите площадь и периметр.

На этой странице сайта, в категории Математика размещен ответ на вопрос Боковая сторона равнобедренного треугольника делится точкой касания вписанной окружности в отношении 2 : 7считая от вершины угла при основании треугольника найдите стороны треугольник если периметр ра?. По уровню сложности вопрос рассчитан на учащихся 5 — 9 классов. Чтобы получить дополнительную информацию по интересующей теме, воспользуйтесь автоматическим поиском в этой же категории, чтобы ознакомиться с ответами на похожие вопросы. В верхней части страницы расположена кнопка, с помощью которой можно сформулировать новый вопрос, который наиболее полно отвечает критериям поиска. Удобный интерфейс позволяет обсудить интересующую тему с посетителями в комментариях.

Видео:Боковая сторона равнобедренного треугольника равна 5 ... | ОГЭ 2017 | ЗАДАНИЕ 9 | ШКОЛА ПИФАГОРАСкачать

Узнать ещё

Знание — сила. Познавательная информация

Видео:Геометрия В равнобедренный треугольник вписана окружность Точка касания делит боковую сторонуСкачать

Окружность, вписанная в равнобедренный треугольник

Если в задача дана окружность, вписанная в равнобедренный треугольник, в ее решении могут быть использованы свойства касательных и свойство биссектрисы треугольника.

Центр вписанной в треугольник окружности является точкой пересечения его биссектрис. Поскольку в равнобедренном треугольнике биссектриса, проведенная к основанию, совпадает с медианой и высотой, то центр вписанной в равнобедренный треугольник окружности лежит на высоте и медиане, проведенных к основанию .

Рассмотрим две задачи на вписанную в равнобедренный треугольник окружность.

Боковая сторона равнобедренного треугольника делится точкой касания вписанной окружности в отношении 8:9, считая от вершины угла при основании треугольника. Найти площадь треугольника, если радиус вписанной окружности равен 16 см.

окружность (O, r) — вписанная,

F, K, M, — точки касания со сторонами AB, BC, AC,

1) Пусть k — коэффициент пропорциональности (k>0). Тогда AM=8k см, MC=9k см.

2) По свойству касательных, проведенных из одной точки,

AF=AM=8k см, CK=MC=9k см.

Так как AC=BC, то BK=AM и BF=BK=8k см.

3) Центр вписанной окружности является точкой пересечения биссектрис треугольника.

Так как ∆ ABC — равнобедренный с основанием AB, то CF — высота, медиана и биссектриса ∆ ABC.

4) Рассмотрим треугольник AFC.

∠AFC=90, AF=8k см, AC=AM+MC=17k см.

OF=r. Пусть CO=x см, тогда

CO=34 см, CF=CO+OF=34+16=50 см.

По теореме Пифагора:

Ответ: 1333 1/3 кв.см.

Центр окружности, вписанной в равнобедренный треугольник, делит высоту, проведенную к основанию, в отношении 5:4. Найти периметр треугольника, если боковая сторона меньше основания на 15 см.

Дано: ∆ ABC, AC=BC,

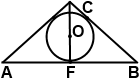
окружность (O, r) — вписанная,

CF — высота, CO:OF=5:4, AC

1) Рассмотрим ∆ ACF — прямоугольный (так как CF — высота треугольника по условию).

Центр вписанной в треугольник окружности есть точка пересечения его биссектрис.

По свойству биссектрисы треугольника,

Пусть k — коэффициент пропорциональности, тогда AC=5k см, AF=4k см, AB=2AF=8k см.

Следовательно, AC=BC=5∙5=25 см, AB=8∙5=40 см.

🎥 Видео

Задача 6 №27909 ЕГЭ по математике. Урок 129Скачать

12.41.1. Планиметрия. Гордин Р.К.Скачать

№689. В равнобедренном треугольнике основание равно 10 см, а боковая сторона равна 13 смСкачать

Задание 16 ЕГЭ по математике #6Скачать

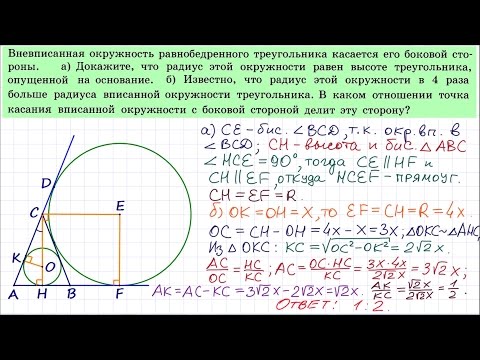
6.4 - Геометрия 7-9 класс ПогореловСкачать

Нафиг теорему синусов 3 задание проф. ЕГЭ по математике (часть II)Скачать

Вписанная и описанная около равнобедренного треугольника, окружностьСкачать