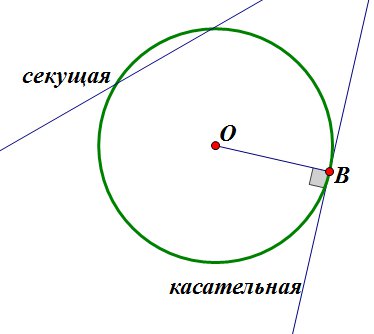
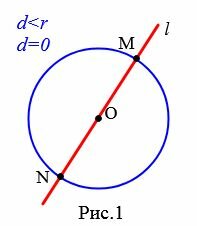
Каково взаимное расположение прямой и окружности (5 видео)

Взаимное расположение прямой и окружности

Выясним количество общих точек прямой и окружности в зависимости от их взаимного расположения. Если прямая l проходит через центр O окружности (Рис.1), то она пересекает окружность в двух точках, которые являются концами диаметра окружности.

Пусть прямая не проходит через центр окружности. Проведем перпендикуляр OH к прямой l (Рис.2, Рис.3, Рис.4). Обозначим расстояние от центра окружности до прямой l буквой d. Рассмотрим сколько общих точек будут иметь прямая и окружность в зависимости от соотношения d и r.

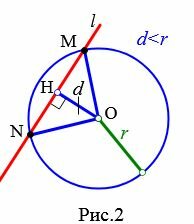Каково взаимное расположение прямой и окружности

Теорема 1. Если расстояние от центра окружности до прямой меньше радиуса окружности, то прямая и окружность имеют две общие точки.

В этом случае прямая называется секущей по отношению к окружности.

Доказательство. Пусть расстояние от центра окружности до прямой меньше радиуса окружности: d Теорема 2. Если расстояние от центра окружности до прямой равно радиусу окружности, то прямая и окружность имеют одну общую точку.

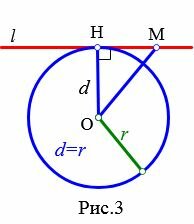Доказательство. Пусть расстояние от центра окружности до прямой равно радиусу окружности: d=r (Рис.3). В этом случае OH=r, т.е. точка H лежит на окружности и является общей точкой прямой l и окружности. Возьмем на прямой l любую точку M отличной от H. Тогда расстояние от OM больше расстояния OH=r, поскольку наклонная OM больше перпендикуляра OH к прямой l. Следовательно точка M не лежит на окружности. Получили, что точка H единственная общая точка прямой l и окружности.

Теорема 3. Если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не имеют общую точку.

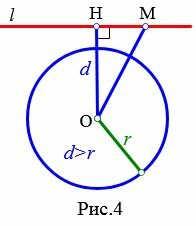Доказательство. Пусть расстояние от центра окружности до прямой больше радиуса окружности:d>r (Рис.4). Тогда ( small OH > r). Возьмем на прямой l любую точку M отличной от H. Тогда ( small OM > OH>r). Следовательно точка M не лежит на окружности. Таким образом, если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не имеют общую точку.

Содержание

Окружность. Взаимное расположение прямой и окружности
«Управление общеобразовательной организацией: новые тенденции и современные технологии»
Взаимное расположение прямой и окружности
📹 Видео

Видео:Взаимное расположение окружности и прямой. 7 класс.Скачать

Окружность. Взаимное расположение прямой и окружности

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Видео:Геометрия 8 класс (Урок№25 - Взаимное расположение прямой и окружности.)Скачать

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»

Свидетельство и скидка на обучение каждому участнику

Учитель: Диденко Т.Р.

Класс: 8 Б класс

Тема: «Окружность. Взаимное расположение прямой и окружности.»

Тип урока: Урок первичного предъявления новых знаний.

Содержательная цель урока: Ввести определения окружности, радиуса, хорды и диаметра. Познакомить с тремя случаями взаимного расположения прямой и окружности. Обучить использовать полученные на уроке факты, определения для решения задач.

Дидактические цели (УУД):

— уметь устанавливать причинно-следственные связи, строить логическое рассуждение, делать умозаключения и выводы на протяжении всего урока;

— умение анализировать объекты и выделять существенные признаки;

— умение находить информацию в тексте (чтение и работа с информацией);

— использовать знаково-символические средства (модели) для решения задач;

— извлекать информацию и перерабатывать ее.

— умение ставить и сохранять на протяжение всего урока учебную задачу;

— планировать свои действия в соответствии с поставленной задачей;

— осуществление итогового и пошагового контроля по результату;

— преобразовывать познавательную задачу в практическую.

— учитывают разные мнения и стремления к координации различных позиций в сотрудничестве;

— умение работать в группе – договариваться и приходить к общему решению;

— умение строить монологическое высказывание;

— формулировать собственное мнение и позицию.

— формирование учебно-познавательного интереса к новому учебному материалу;

— формирование причин успеха и неуспеха в учебной деятельности;

— формирование самооценки, основных моральных норм.

1. Учебник «Геометрия 7-9», автор Атанасян Л.С.

2. ПК, раздаточный материал

3. Циркуль, линейка.

1. Организационный момент

2. Мотивация учебной деятельности

3. Актуализация знаний

4. Постановка проблемы

5. Открытие нового знания

6. Применение нового знания

8. Домашнее задание

1. Организационный момент (1 мин)

Приветствие. Проверка готовности к уроку

1. Мотивация учебной деятельности (2 мин)

— Сегодня урок, посвятим изучению материала, основы которого вы уже изучали в 7 классе. А материал этот относится к одной из древнейших геометрических фигур, считавшейся самой совершенной. Представление о ней дает также линия движения вращающейся модели самолета, соединенной шнуром с рукой человека или обода колеса, спицы которого относятся к элементам этой геометрической фигуры.

— Может, кто-то уже догадался, о какой линии, геометрической фигуре идёт речь?

(Если ученики не догадываются, то учитель делает ещё попытки их натолкнуть).

— Правильно, это окружность!

1. Актуализация знаний (4 мин)

— Итак, для начала введем определение окружности, продолжите фразу окружность – это… (ученики приводят свои варианты определения).

— Давайте запишем точное определение. Окружность – это фигура, состоящая из всех точек плоскости, находящихся на заданном расстоянии от заданной точки.

— А что это за заданное расстояние и точка? (Ученики высказывают свои предположения)

— Правильно! Заданное расстояние – это радиус окружности, а заданная точка – это центр окружности. Давайте введем точное определение радиуса. Радиус – это отрезок, соединяющий центр с любой точкой окружности.

— Чем отличается окружность от круга? (Ученики отвечаю).

Вспомним, как задается окружность.

— Скажите с помощью какого инструмента можно построить окружность?

— Для построения окружности необходимо определить?

Чертим окружность (рис.1). Вводим обозначения хорды, диаметра. Хорда – отрезок, соединяющий две точки окружности. Диаметр – хорда, проходящая через центр окружности.

— Хорошо, а как называются отрезки АВ, ВС, ОК, CD ?

— Давайте теперь потренируемся находить диаметр, хорды на окружности. (Задание №1 из раздаточного материала. Работа с классом. Приложение 1).

— Что можно сказать о взаимном расположении точек и окружности, изображенных на чертеже?

— Давайте попробуем сформулировать задачу урока.

4. Постановка проблемы (4 мин)

— Как вы думаете, сколько общих точек может иметь прямая и окружность?

— На этот вопрос я предлагаю вам ответить совместно, работая в группах.

— Подумайте, как могут располагаться по отношению друг к другу прямая и окружность. Правильно, три, давайте нарисуем эти случаи и проверим, сколько они имеют общих точек!

На доске приготовлен чертеж 3 окружностей. Рис.2

Рис.2 Взаимное расположение прямой и окружности. а) прямая пересекает окружность б) прямая касается окружности в) прямая не пересекается с окружность.

— Итак, сделаем вывод: сколько случаев у нас получилось?

— А теперь подумайте, от чего зависит то, что окружность и прямая имеют две или одну общую точку или не имеют их совсем.

— Давайте вспомним, что же является расстоянием от точки до прямой?

5. Открытие новых знаний (14 мин)

— Итак, рассмотрим подробнее все эти случаи. Исследуем взаимное расположение прямой и окружности в первом случае (Рис.2а). Расстояние от центра окружности до прямой обозначим буквой d.

— Что можно сказать про d и r в этом случае? Как бы вы назвали прямую АВ в соответствии с ее расположением относительно окружности?

— Правильно, d r , прямая пересекает окружность в 2 точках. Такая прямая называется секущей.

— Исследуем взаимное расположение прямой и окружности во втором случае (рис.2б).

— Что можно сказать про d и r в этом случае? Как бы вы назвали прямую н в соответствии с ее расположением относительно окружности?

— Правильно, d = r , прямая имеет с окружностью 1 общую точку. Такая прямая называется касательной . Попробуйте дать самостоятельно определение касательной. Проверим истинность вашего высказывания, обратившись к учебнику на странице 166.

— Исследуем взаимное расположение прямой и окружности в третьем случае (рис.2в).

— Что можно сказать про d и r в этом случае? D > r , прямая не имеет с окружностью общих точке.

Итак, сделаем вывод. Каково взаимное расположение прямой и окружности? От чего зависит взаимное расположение прямой и окружности. (Отвечают ученики).

6. Применение нового знания (10 мин )

— Теперь нам необходимо наши с вами знания применить на практике. (Задание №2 самостоятельно из раздаточного материала (Приложение 1). На выполнение задания отводится 2 мин. Проверка задания. Учащиеся озвучивают свои ответы.

— Теперь попытаемся решить задачи с использованием новых знаний. (Учащиеся делятся на две группы, одни решают задание №3(а), другие задание №3(б) (Приложение 1)). На задание отводится 5 мин. После по одному человеку из группы выходят к доске и демонстрируют решение. Проверка.

7. Рефлексия (3 мин)

— А теперь подведем итоги нашего урока.

— Давайте вернемся к началу урока и вспомним, какую задачу мы себе поставили.

— Какое взаимное расположение прямой и окружности вы сегодня узнали?

— Какая прямая называется касательной к окружности?

— Для того чтобы проверить свои знания по пройденному сегодня материалу, выполним небольшой тест.

— Ребята обратите внимание на доску, там написаны начала фраз, закончите эти фразы:

1) я могу оценить свою работу …;

2) я впервые понял что …

8. Домашнее задание (1 мин)

— Теперь запишите домашнее задание: П.68, № 633.

— Спасибо за урок, до свидания!

Тема открытого урока: «Окружность. Взаимное расположение прямой и окружности.»

Найдите на рис.1: а) диаметр б) все радиусы в) все хорды

Выясните взаимное расположение прямой и окружности, если

1. R=15 см , d=11 см

2. R=6 см , d=5,2 см

4. R=7 см , d=0,5д м

5. R=4 см , d=40м м

Найдите расстояние от точки А до ближайшей к ней точки окружности с центром О и радиусом r , если 1) ОА = 12см, r = 8см, 2) ОА = 6см, r = 8 см.

R =5см. Найдите расстояние от центра окружности до прямой, содержащей хорду, равную 8 см.

Видео:8 класс, 31 урок, Взаимное расположение прямой и окружностиСкачать

Взаимное расположение прямой и окружности

Существует 3 случая взаимного расположения прямой и окружности в зависимости от соотношения между радиусом r окружности и расстоянием d прямой от центра окружности.

1. d r. Если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не имеют общих точек.

Прямая, имеющая с окружностью ровно одну общую точку, называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности. Прямая, имеющая с окружностью две общие точки, называется секущей.

Теоремы о касательных и секущих

Касательная к окружности перпендикулярна радиусу, проведенному к точке касания.

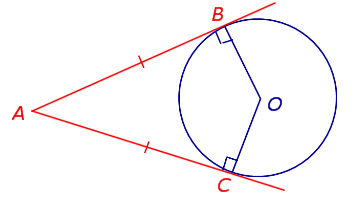
Если из данной точки проведены к окружности две касательные, то отрезки касательных равны между собой и центр окружности лежит на биссектрисе угла с вершиной в этой точке: (AB=AC) .

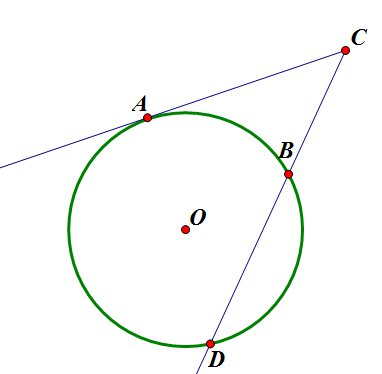
Если из данной точки проведены к окружности касательная и секущая, то квадрат длины отрезка касательной равен произведению всего отрезка секущей на его внешнюю часть: (AC^2=CDcdot BC) .

Произведение всего отрезка одной секущей на его внешнюю часть равно произведению всего отрезка другой секущей на его внешнюю часть: (ACcdot BC=ECcdot DC) .