Биссектриса перпендикулярна медиане треугольника свойства

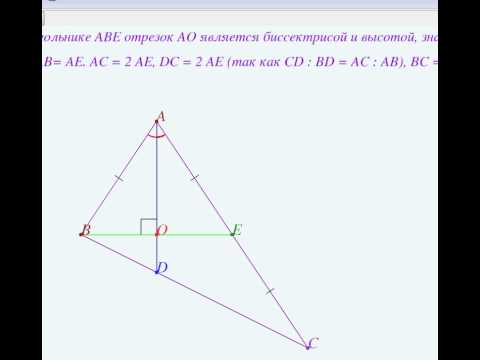
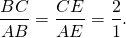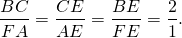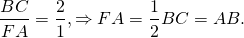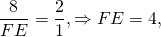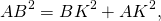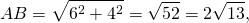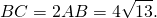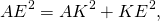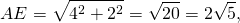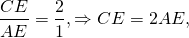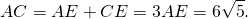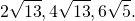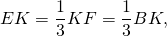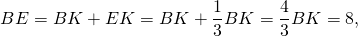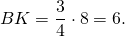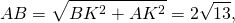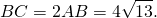В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 8.

Найти стороны треугольника ABC.

Дано: ΔABC,

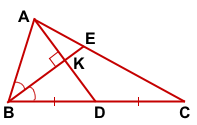
AD — медиана, BE — биссектриса,

Так как в треугольнике ABD BK — биссектриса и высота, то ΔABC — равнобедренный с основанием AD (по признаку равнобедренного треугольника). Значит, AB=BD. Следовательно, BC=2AB.

По свойству равнобедренного треугольника BK — медиана и AK=KD=4.

3) По свойству биссектрисы треугольника в ΔABC

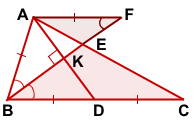
3) Проведём через точку A прямую, параллельную BC и продлим BE до пересечения с этой прямой в точке F.

Рассмотрим треугольники BEC и FEA.

∠AFB=∠CBF (как внутренние накрест лежащие при BC || AF и секущей BF).

Значит треугольники BEC и FEA подобны (по двум углам).

Из подобия треугольников следует пропорциональность соответствующих сторон:

Таким образом, треугольник ABF — равнобедренный с основанием BF, а значит, его высота AK является также медианой и BK=KF.

4) Рассмотрим прямоугольный треугольник ABK. По теореме Пифагора

5) Рассмотрим прямоугольный треугольник AKE.

KE=BE-BK=8-6=2. По теореме Пифагора

1) Пусть AD∩BE=K.

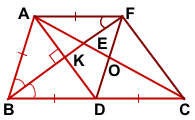
Так как в треугольнике ABD BK — биссектриса и высота, то ΔABC — равнобедренный с основанием AD (по признаку равнобедренного треугольника). Значит, AB=BD.

По свойству равнобедренного треугольника BK — медиана и AK=KD=4.

2) Отложим на луче BE с другой стороны от точки K отрезок KF, KF=BK.

Проведём отрезки DF и CF.

Четырёхугольники AFDB и AFCD — параллелограммы (по признаку параллелограмма). Тогда AF=BD, DF=AB, FC=AD (по свойству параллелограмма), а так как AB=BD, то ABCD — ромб.

AC∩DF=O. По свойству параллелограмма O — середина DF. Значит E — точка пересечения медиан треугольника AFD. По свойству медиан FE:EK=2:1. Следовательно

3) Из треугольника ABK по теореме Пифагора

4) Так как сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон, в параллелограмме AFCD

Видео:7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать

Свойство биссектрисы и медианы треугольника

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

«Актуальность создания школьных служб примирения/медиации в образовательных организациях»

Свидетельство и скидка на обучение каждому участнику

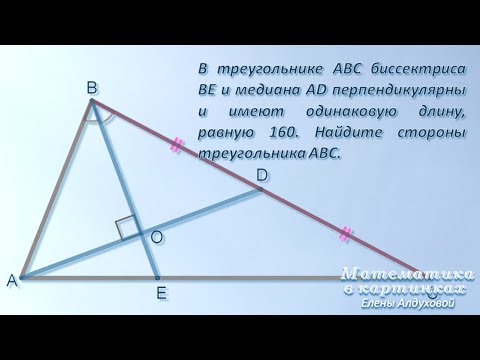
Задание 26. В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 8. Найдите стороны треугольника ABC.

1. По условию задачи биссектриса BE и медиана AD пересекаются под прямым углом. Следовательно, в треугольнике ABD BO – медиана, и треугольник ABD равнобедренный с основанием AD. Тогда AO = OD = 4.

Если медиана с биссектрисой перпендикулярны, то в точке пересечения биссектриса делится в отношении 3:1, считая от вершины (по доказанной выше теореме), следовательно, BO = , OE = BE = 8 = 2

2. Рассмотрим прямоугольный треугольник AOB, в котором известны два катета AO и BO. По теореме Пифагора найдем гипотенузу AB:

Так как BD = AB, а BC = 2BD = 2AB, то BC =2∙ 2 = 4

3. Вычислим длину отрезка AE из прямоугольного треугольника AOE по теореме Пифагора: AE = = = = 2

По свойству биссектрисы треугольника =

и сторона AC = AE + EC = 2 + = 6

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 976 человек из 78 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 308 человек из 70 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 677 человек из 74 регионов

Ищем педагогов в команду «Инфоурок»

Видео:Высота, биссектриса, медиана. 7 класс.Скачать

Дистанционные курсы для педагогов

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 550 689 материалов в базе

Материал подходит для УМК

«Геометрия», Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др.

§ 3. Применение подобия к доказательству теорем и решению задач

Другие материалы

• 26.11.2017
• 2124
• 13

• 26.11.2017
• 2075
• 18

• 25.11.2017
• 462
• 0

• 25.11.2017
• 1000
• 2

• 25.11.2017
• 362
• 2

• 25.11.2017
• 1421
• 14

• 25.11.2017
• 2675
• 31

• 25.11.2017
• 2662
• 4

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 26.11.2017 5827
• DOCX 55.6 кбайт
• 19 скачиваний
• Рейтинг: 5 из 5
• Оцените материал:

Настоящий материал опубликован пользователем Туаева Марина Григорьевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 4 года и 2 месяца
• Подписчики: 0
• Всего просмотров: 16217
• Всего материалов: 9

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:Свойство биссектрисы треугольника с доказательствомСкачать

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Школьники в Пензенской области с 7 по 14 февраля уйдут на внеплановые каникулы

Время чтения: 2 минуты

В «Единой России» предложили ввести раздел безопасности детей в интернете в курс ОБЖ

Время чтения: 3 минуты

В Египте нашли древние школьные «тетрадки»

Время чтения: 1 минута

Петербургская учительница уволилась после чтения на уроке Введенского и Хармса

Время чтения: 3 минуты

У 76% российских учителей оклад ниже МРОТ

Время чтения: 2 минуты

Полный перевод школ на дистанционное обучение не планируется

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Видео:Как найти длину биссектрисы, медианы и высоты? | Ботай со мной #031 | Борис ТрушинСкачать

Биссектриса перпендикулярна медиане треугольника свойства

Ключевые слова: основные линии треугольника, медиана, биссектриса, высота, средния линия, серединные перпендикуляры

Рассмотрим произвольный треугольник ABC:

a, b, c — стороны треугольника

$$m_a$$ — медиана к стороне a угла A

$$h_a$$ — высота к стороне a угла A

$$l_a$$ — биссектриса к стороне a угла A

Медиана треугольника — это отрезок, соединяющий верщину треугольника с серединой противолежащей стороны этого треугольника.

Свойства медиан треугольника

• Медиана разбивает треугольник на два треугольника одинаковой площади.
• Медианы треугольника пересекаются в одной точке, которая делит каждую из них в отношении 2:1, считая от вершины. Эта точка называется центром тяжести треугольника.
• Весь треугольник разделяется своими медианами на шесть равновеликих треугольников.

Биссектриса угла — это луч, который исходит из его вершины, проходит между его сторонами и делит данный угол пополам.
Биссектрисой треугольника называется отрезок биссектрисы угла треугольника, соединяющий вершину с точкой на противолежащей стороне этого треугольника.

Свойства биссектрис треугольника

• Биссектриса угла — это геометрическое место точек, равноудаленных от сторон этого угла.
• Биссектриса внутреннего угла треугольника делит противолежащую сторону на отрезки, пропорциональные прилегажащим сторонам.
• Точка пересечения биссектрис треугольника является центром окружности, вписанной в этот треугольник.

Высотой треугольника называется перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону этого треугольника.

Свойства высот треугольника

• В прямоугольном треугольнике высота, проведенная из вершины прямого угла, разбивает его на два треугольника, подобные исходному.
• В остроугольном треугольнике две его высоты отсекают от него подобные треугольники.
• Если треугольник остроугольный, то все основания высот принадлежат сторонам треугольника, а у тупоугольного треугольника две высоты попадают на продолжение сторон
• Три высоты в остроугольном треугольнике пересекаются в одной точке и эту точку называют ортоцентром треугольника.

Свойства серединных перпендикуляров треугольника

• Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка. Верно и обратное утверждение: каждая точка, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к нему.
• Точка пересечения серединных перпендикуляров, проведенных к сторонам треугольника, является центром окружности, описанной около этого треугольника.

Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.

Свойство средней линии треугольника

• Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.

🎥 Видео

8. Медиана треугольника и её свойства.Скачать

Биссектриса перпендикулярна медианеСкачать

Геометрия 7 класс (Урок№12 - Медианы треугольника. Биссектрисы треугольника. Высоты треугольника.)Скачать

3 свойства биссектрисы #shortsСкачать

25 задание ОГЭ ✧ В ∆ABC биссектриса BE и медиана AD перпендикулярны и ... #огэ #егэ #геометрияСкачать

🔥 Свойства МЕДИАНЫ #shortsСкачать

Геометрия В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длинуСкачать

ЕГЭ 2024 по математике. №1,17 Медиана, биссектриса, высота, серединный перпендикулярСкачать

Равнобедренный треугольник. Свойства равнобедренного треугольника | Математика | TutorOnlineСкачать

БИССЕКТРИСА, МЕДИАНА, ВЫСОТА; Основные свойства (теория) | МатематикаСкачать

8 класс, 35 урок, Свойства биссектрисы углаСкачать

17. Медианы, биссектрисы и высоты треугольникаСкачать

ОГЭ, задание #26, вариант-8Скачать

Свойства биссектрисы треугольникаСкачать

Формула для биссектрисы треугольникаСкачать

Медианы, биссектрисы и высоты треугольника | Геометрия 7-9 класс #18 | ИнфоурокСкачать