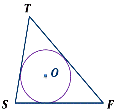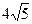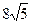Выбери треугольник который описан около окружности (3 видео)

Выбери треугольник который описан около окружности

Вопрос по геометрии:

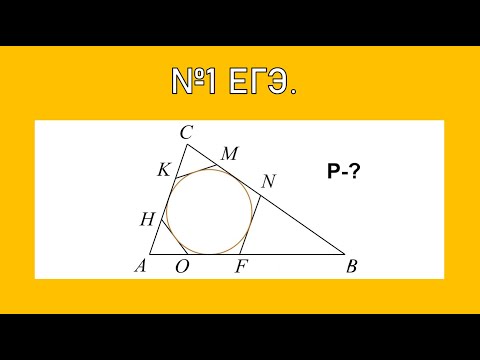
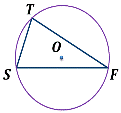
Найди треугольник, который описан около окружности.

Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?

Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!

Содержание

Как написать хороший ответ?
Тест: Вписанная и описанная окружности
Вписанные и описанные треугольники. Еще две формулы площади треугольника. Теорема синусов
🎥 Видео

Ответы и объяснения 1

Знаете ответ? Поделитесь им!

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
Писать без грамматических, орфографических и пунктуационных ошибок.

Этого делать не стоит:

Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
Использовать мат — это неуважительно по отношению к пользователям;
Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Геометрия.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!

Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Тест: Вписанная и описанная окружности

Вписанная и описанная окружности

В равнобедренном треугольнике точка касания вписанной окружности делит боковую сторону на отрезки длиной 12 см и 3 см, считая от отнования. Найдите площадь треугольника. (в ответе укажите только число без единицы измерения)

Дополните определение:
Если все стороны многоугольника касаются окружности, то окружность называется .

Если около четырехугольника можно описать окружность, то .

Выберите один из 4 вариантов ответа:

1) сумма противоположных углов равна 180 0 .

2) суммы противоположных сторон равны.

3) суммы смежных сторон равны.

4) сумма соседних углов равна 180 0 .

Какие из данных многоугольников описаны около окружности?

Выберите несколько из 3 вариантов ответа:

Найдите стороны остроугольного равнобедренного треугольника, если высота, проведенная к его основанию, равна 8 см, а радиус окружности, в которую он вписан 5 см.

Выберите несколько из 5 вариантов ответа:

Дополните определение:
Если все вершины многоугольника лежат на окружности, то окружность называется .

Окружность можно вписать в любой треугольник?

Выберите один из 5 вариантов ответа:

1) только в равносторонний.

2) в треугольник нельзя вписать окружность.

4) только в равнобедренный.

5) только в прямоугольный.

Если в четырехугольник можно вписать окружность, то .

Выберите один из 4 вариантов ответа:

1) суммы его смежных сторон равны.

2) сумма соседних углов равна 180 0 .

3) сумма противоположных углов равна 180 0 .

4) суммы его противоположных сторон равны.

Выберите верные утверждения:

Выберите несколько из 5 вариантов ответа:

1) Треугольник нельзя описать около окружности.

2) Около квадрата нельзя описать окружность.

3) Прямоугольник нельзя описать около окружности.

4) Около прямоугольника можно описать окружность.

5) Ромб можно описать около окружности.

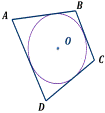
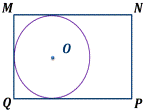
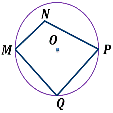
Какие из данных многоугольников вписаны в окружность?

Выберите несколько из 3 вариантов ответа:

Видео:Задача 6 №27916 ЕГЭ по математике. Урок 133Скачать

Вписанные и описанные треугольники. Еще две формулы площади треугольника. Теорема синусов

Вписанный треугольник — треугольник, все вершины которого лежат на окружности. Тогда окружность называется описанной вокруг треугольника.

Очевидно, расстояние от центра описанной окружности до каждой из вершин треугольника одинаково и равно радиусу этой окружности.

Вокруг любого треугольника можно описать окружность, причем только одну.

Окружность вписана в треугольник, если она касается всех его сторон. Тогда сам треугольник будет описанным вокруг окружности. Расстояние от центра вписанной окружности до каждой из сторон треугольника равно радиусу этой окружности.

В любой треугольник можно вписать окружность, причем только одну.

Попробуйте сами описать окружность вокруг треугольника и вписать окружность в треугольник.

Как вы думаете, почему центр вписанной окружности — это точка пересечения биссектрис треугольника, а центр описанной окружности — точка пересечения серединных перпендикуляров к его сторонам?

В задачах ЕГЭ чаще всего встречаются вписанные и описанные правильные треугольники.

Есть и другие задачи. Для их решения вам понадобятся еще две формулы площади треугольника, а также теорема синусов.

Вот еще две формулы для площади.
Площадь треугольника равна половине произведения его периметра на радиус вписанной окружности.

— радиус окружности, вписанной в треугольник.

Есть и еще одна формула, применяемая в основном в задачах части :

где — стороны треугольника, — радиус описанной окружности.

Для любого треугольника верна теорема синусов:

Ты нашел то, что искал? Поделись с друзьями!

. Радиус окружности, вписанной в равнобедренный прямоугольный треугольник, равен . Найдите гипотенузу c этого треугольника. В ответе укажите .

Треугольник прямоугольный и равнобедренный. Значит, его катеты одинаковы. Пусть каждый катет равен . Тогда гипотенуза равна .

Запишем площадь треугольника АВС двумя способами:

Приравняв эти выражения, получим, что . Поскольку , получаем, что . Тогда .

В ответ запишем .

. Сторона АС треугольника АВС с тупым углом В равна радиусу описанной около него окружности. Найдите угол В. Ответ дайте в градусах.

По теореме синусов,

Получаем, что . Угол — тупой. Значит, он равен .

. Боковые стороны равнобедренного треугольника равны , основание равно . Найдите радиус описанной окружности этого треугольника.

Углы треугольника не даны. Что ж, выразим его площадь двумя разными способами.

, где — высота треугольника. Ее найти несложно — ведь в равнобедренном треугольнике высота является также и медианой, то есть делит сторону пополам. По теореме Пифагора найдем . Тогда .

Задачи на вписанные и описанные треугольники особенно необходимы тем, кто нацелен на решения задания .