в треугольнике BC = 5 см, а две другие стороны треугольника больше BC соответственно на 2 см и на 4 см
в четырёхугольнике три другие стороны больше DE соответственно на 3 см, 5 см и 6 см
сколько вершин у получившегося многоугольника?
найдите периметр получившегося многоугольника
- Ответы на вопрос
- Даны выпуклые треугольник abc и четырехугольник dekm к стороне треугольника
- Источник задания: Решение 4351. ЕГЭ 2016 Математика, И.В. Ященко. 30 вариантов. Ответ.
- На стороне ВС выпуклого четырехугольника ABCD отмечена точка М, а вне четырехугольника — точка К так, что пары отрезков АК и ВМ, KD и МС
- Ваш ответ
- решение вопроса
- Похожие вопросы
- 🌟 Видео
Видео:8 класс, 2 урок, Выпуклый многоугольникСкачать

Ответы на вопрос
гипотенуза по теореме пифагора равна
радиус вписанной окружности равен
площадь треугольника равна половине произведения катетов
площадь круга равна
sфигуры вне круга=s-sкр
sфигуры вне круга=6-pi кв.см
это вряд ли, насчет корня из трех, сейчас поглядим.
ясно, что сторона квадрата равна диаметру, то есть радиус окружности 2.
центральный угол, соответтствующий стороне вписанного пятиугольника равен 360/5 = 72 градуса., отсюда половина стороны равна r*sin(72/2) = 2*sin(36), а периметр, соответственно, 10*sin(36);
уж и не знаю, не похоже это на 9*корень( сейчас попробую вычислить.
ну, не равно, конечно, синус 36 градусов выражается через корень из 5 :
ответ для перметра 5*корень(5/2 — (1/2)*корень(
приводить вычисления синуса 36 градусов я тут не буду. вполне достаточно 10*sin(36).
между прочим, приближенно периметр будет 5,87785252292473,
а 9*корень(3) = 15,5884572681199, это почти в 3 раза больше.
все таки напишу, как синус вычисляется, для 18 градусов.
cos(18) = sin(72) = 2*cos(36)*sin(36) = 4*cos(36)*sin(18)*cos(18);
пусть х = sin(18); тогда
здесь самый трудный момент, этот кубический многочлен имеет один рациональный корень 1/2 (кстати, это наводит на мысль о существовании построения угла в 18 градусов на основании прямоугольного треугольника с углами 30 и 60, это надо обдумать). раз 1/2 — корень, то этот многочлен нацело делится на
то есть представим в виде (это окончательный результат)
8*x^3 — 4*x +1 = (2*х — 1)*(4*х^2 + 2*x — 1) = 0;
у квадратного многочлена
два корня, один из них — положительный
х1 = (корень(5) — 1)/4;
это и есть sin(18). вычислить теперь косинус, перемножить и умножить на 2 совсем не сложно, ответ я уже приводил.
надо же, как интересно! если построить равнобедренный треугольник с углами 72, 72 и 36 (приятное совпадение), то биссектриса угла 72 градуса делит его (треугольник) на 2 равнобедренных треугольника, один из которых (содержащий основание) подобен исходному, сама биссектриса же при этом равна основанию и отрезку боковой стороны, который она отсекает, — дальнему от основания (а докажите! : отсюда легко получить выражение величин углов 18, 36 и 72 градуса. но это — сами :
так диоганали взаимноперпендикулярны, то этот четырехугольник либо ромб, либо квадрат. в обоих случаях площадь равна половине произведения диогоналей.
Видео:Сумма внутренних углов многоугольника. Выпуклые и невыпуклые многоугольники. 8 класс.Скачать

Даны выпуклые треугольник abc и четырехугольник dekm к стороне треугольника
Видео:№194. Начертите треугольник. Через каждую вершину этого треугольника с помощью чертежногоСкачать

Источник задания: Решение 4351. ЕГЭ 2016 Математика, И.В. Ященко. 30 вариантов. Ответ.
Задание 16. Дан выпуклый четырёхугольник ABCD со сторонами АВ = 5, ВС = CD = 3, AD = 8 и диагональю АС = 7.
а) Докажите, что около него можно описать окружность.
б) Найдите диагональ BD.
а) Если вокруг четырехугольника можно описать окружность, то сумма его противоположных углов будет равна 180 градусов. Это необходимое и достаточное условие для доказательства этого положения. Докажем, что сумма углов 

Аналогично для угла 
Таким образом получаем, что

то есть вокруг данного четырехугольника можно описать окружность.
б) Рассмотрим треугольник ABD и по теореме косинусов можно записать:
Также диагональ BD можно вычислить по теореме косинусов из треугольника BCD:
Вычтем (1) и (2), получим:
Подставим это значение в (2), найдем BD:

Ответ: 
Видео:№154. Дан треугольник ABC. Постройте: а) биссектрису АК; б) медиану ВМ; в) высоту СН треугольника.Скачать

На стороне ВС выпуклого четырехугольника ABCD отмечена точка М, а вне четырехугольника — точка К так, что пары отрезков АК и ВМ, KD и МС
Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Ваш ответ
Видео:№973. Даны координаты вершин треугольника ABC: А (4; 6), В (-4; 0), С (-1; -4). Напишите уравнениеСкачать

решение вопроса
Видео:САМЫЙ СТРАННЫЙ ПРИМЕР 3 задания проф. ЕГЭ по математикеСкачать

Похожие вопросы
- Все категории
- экономические 43,277
- гуманитарные 33,618
- юридические 17,900
- школьный раздел 606,712
- разное 16,823
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
🌟 Видео
№371. Докажите, что выпуклый четырехугольник ABCD является параллелограммом,Скачать

Задача на подобие треугольников. А ты сможешь решить? | TutorOnline | МатематикаСкачать

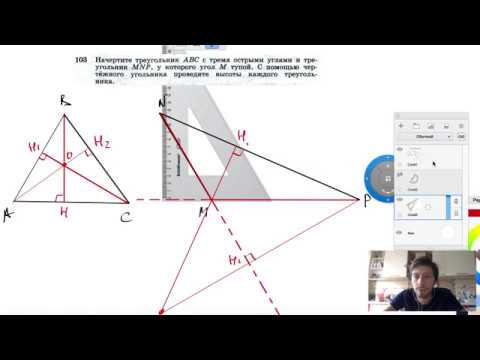
№103. Начертите треугольник ABC с тремя острыми углами и треугольник MNP, у которого угол М тупой.Скачать
Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

Задача 6 №27357 ЕГЭ по математике. Урок 46Скачать

Что такое выпуклый четырёхугольник? | Математика 8 класс | Геометрия 8 класс | МегаШколаСкачать

Задание 3 ЕГЭ по математике. Урок 41Скачать

Задача 6 №27922 ЕГЭ по математике. Урок 139Скачать

Задание 6 ЕГЭ по математике. Урок 17Скачать

ЕГЭ Математика Задание 6#27778Скачать

Задание 6 ЕГЭ по математике. Урок 26Скачать

ОГЭ/База Все прототипы задач с треугольникамиСкачать

Задача 6 №27350 ЕГЭ по математике. Урок 42Скачать









