Объем по длине окружности и высоте (2 видео)

Как рассчитать объем цилиндра

На данной странице калькулятор поможет рассчитать объем цилиндра онлайн. Для расчета задайте высоту, радиус или площадь основания. Вычисления производятся в миллиметрах, сантиметрах, метрах. Результат выводится в кубических сантиметрах, литрах и кубических метров.

Цилиндр — геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её.

Содержание

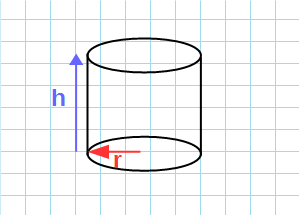
По высоте и радиусу
V = π·r²·h
Через площадь основания и высоту
Строительный клуб
объема в м 3 и литрах
Как рассчитать объем цилиндра ?
Объем цилиндра
Объем правильного цилиндра через радиус и высоту цилиндра
Формулы и калькулятор для вычисления объема цилиндра через площадь основания и высоту цилиндра
Формулы и калькулятор для вычисления объема цилиндра через диаметр основания
Объем цилиндрической полости
Поверхности цилиндра
Сечения цилиндра
Что такое объем
📽️ Видео

По высоте и радиусу

Формула объема цилиндра через высоту и радиус:

V = π·r²·h

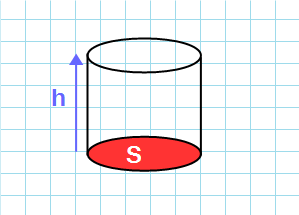
Через площадь основания и высоту

Формула объема цилиндра через высоту и площадь основания:

Видео:11 класс. Геометрия. Объем цилиндра. 14.04.2020Скачать

Строительный клуб

Видео:Длина окружности. Площадь круга. 6 класс.Скачать

объема в м 3 и литрах

Введите диаметр цилиндра в мм

Введите высоту цилиндра в мм:

Объем цилиндра равен:

Видео:Объём цилиндраСкачать

Как рассчитать объем цилиндра ?

Объем цилиндра определятся по формуле:

V=h*Π*d 2 /4, где

h — высота цилиндра (длина цилиндра);

Π = 3.1415926535 — математическая постоянная, равная отношению длины окружности к её диаметру;

d — диаметр основания цилиндра.

Объем цилиндра равен площади основания (круга) умноженной на высоту цилиндра.

Если диаметр и высота цилиндра измерены в мм (миллиметрах), то объем цилиндра в кубических метрах (м3) равен:

V_м3=(h_мм*Π*d_мм 2 /4)/1 000 000 000)

Если диаметр и высота цилиндра измерены в мм (миллиметрах), то объем цилиндра в литрах (л) равен:

V_л=(h_мм*Π*d_мм 2 /4)/1 000 000)

Видео:11 класс. Геометрия. Объем цилиндраСкачать

Объем цилиндра

Объем цилиндра, формулы и калькулятор для вычисления объема цилиндра и площади его поверхностей, а также необходимая теория о характеристиках цилиндра.

Видео:Цилиндр - расчёт площади, объёма.Скачать

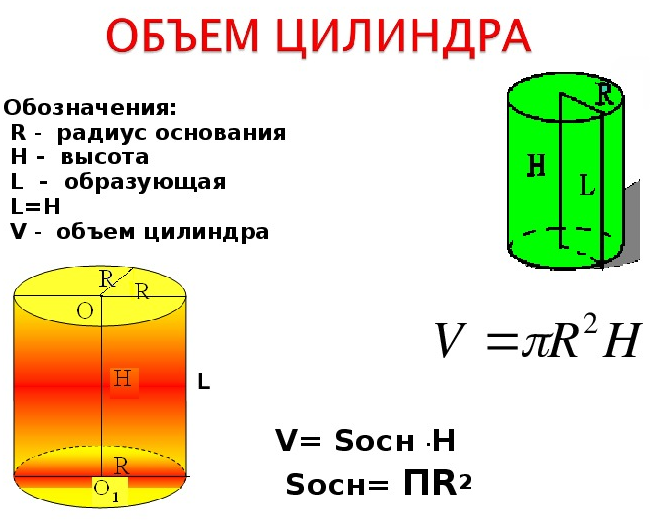
Объем правильного цилиндра через радиус и высоту цилиндра

Видео:Длина окружности. Площадь круга - математика 6 классСкачать

Формулы и калькулятор для вычисления объема цилиндра через площадь основания и высоту цилиндра

Видео:+Как найти длину окружностиСкачать

Формулы и калькулятор для вычисления объема цилиндра через диаметр основания

Видео:Длина окружности. Математика 6 класс.Скачать

Объем цилиндрической полости

Объем полости в виде цилиндра равен объему цилиндра, который извлечен из данной полости для ее образования. То есть для вычисления цилиндрической полости можно воспользоваться формулами и калькулятором для расчета простого правильного цилиндра в зависимости от известных исходных данных.

На картинке продемонстрирована цилиндрическая полость, образованная в теле путем извлечения из него цилиндра. Объем извлеченного цилиндра и объем образованной полости равны.

Нужно отметить один важный момент. Несмотря на равенство объемов извлеченного цилиндра и образованной полости, площади поверхностей данных объектов будут отличаться, так как у образованной цилиндрической полости отсутствует верхняя поверхность. То есть суммарная площадь поверхности образованной цилиндрической полости будет меньше суммарной площади извлеченного цилиндра на одну площадь основания цилиндра.

Цилиндр может быть правильным или наклонным .

Правильный цилиндр – это цилиндр, где угол между образующими боковой поверхности и основанием цилиндра равен 90 градусов.

Неправильный или наклонный цилиндр – это цилиндр, где угол между образующими боковой поверхности и основанием цилиндра отличается от 90 градусов.

Рассмотрим правильный цилиндр.

Цилиндр – это тело, образованное вращением прямоугольника вокруг одной из его сторон. Тело цилиндра ограничено двумя кругами, называемыми основанием цилиндра и боковой цилиндрической поверхностью, которая в развертке представляет собой прямоугольник

Цилиндр можно так же описать как тело, состоящее из двух равных кругов, не лежащих в одной плоскости и параллельных между собой, и отрезков, соединяющих все точки одной окружности, с соответствующими точками другой окружности. Данные отрезки называются образующими цилиндра.

Радиус основания цилиндра, является радиусом цилиндра.

Ось цилиндра – это прямая, соединяющая центра оснований цилиндра.

Высота цилиндра – это перпендикуляр, опущенный от одного основания цилиндра к другому.

Видео:5 класс, 21 урок, Объемы. Объем прямоугольного параллелепипедаСкачать

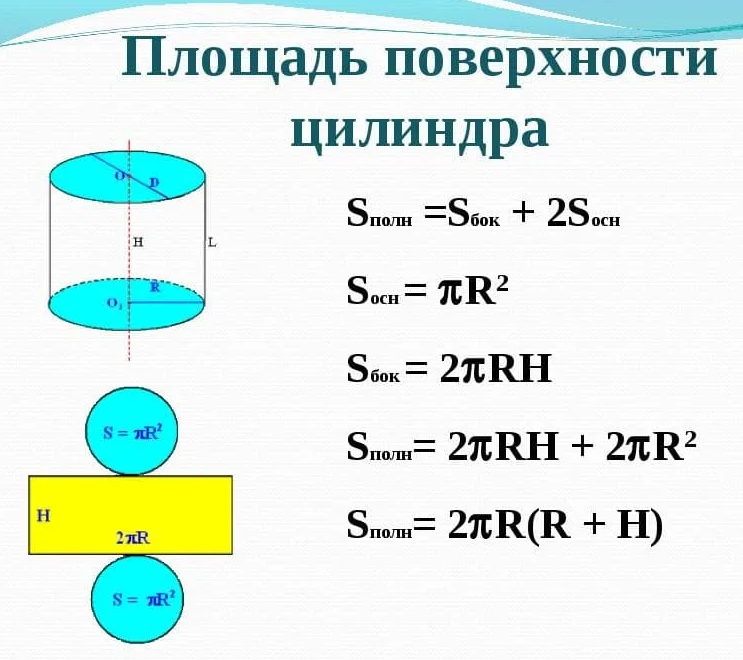
Поверхности цилиндра

Наружную поверхность цилиндра можно условно разделить на три отдельные поверхности: верхняя, нижняя и боковая.

Верхняя и нижняя поверхности цилиндра имеют форму круга и равны между собой.

Боковая поверхность цилиндра имеет форму прямоугольника. Чтобы это наглядно представить, возьмем боковую наружную поверхность цилиндра и мысленно сделаем вертикальный разрез по образующей цилиндра. Далее развернем поверхность на плоскость. В результате увидим, что боковая поверхность имеет форму прямоугольника (см. на картинке).

Видео:Объем цилиндраСкачать

Сечения цилиндра

При сечении цилиндра плоскостью, проходящей через оба основания цилиндра под углом в 90 градусов, всегда получатся прямоугольная фигура .

При сечении цилиндра плоскостью, проходящей через оба основания цилиндра под углом отличным от 90 градусов, получатся фигура, похожая на прямоугольник , но две боковые стороны которого будут являться кривыми линиями.

Если секущая поверхность проходит параллельно основаниям цилиндра, то сечением будет круг .

Если секущая поверхность проходит через боковую поверхность, но при этом не параллельна основанию цилиндра, то в сечении получается эллипс .

Если секущая поверхность проходит через одно основание цилиндра и боковую поверхность, то в сечение будет фигура в виде половины эллипса .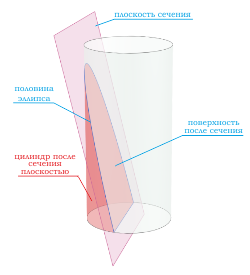

Видео:Длина окружности. Практическая часть - решение задачи. 6 класс.Скачать

Что такое объем

Объем тела (геометрической фигуры) – это количественная характеристика, характеризующая количество пространства, занимаемого телом. Объем выражается в кубических единицах измерения, например: мм 3 , см 3 , мл 3 .

Формула вычисления объема цилиндра часто применяются при расчете массы различных цилиндров, например, прутков, заготовок и т.п. Для вычисления массы, необходимо вычисленный объем цилиндра умножить на плотность материала из которого цилиндр.

Так же, вычислить объём цилиндра иногда требуется для определения полости в виде цилиндра (цилиндрическая полость). В данном случае объём полости будет равен объёму цилиндра, который полностью занимает эту полость.

Объем и площадь других видов цилиндров рассмотрен в статьях: