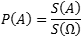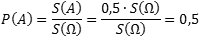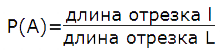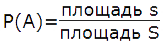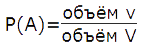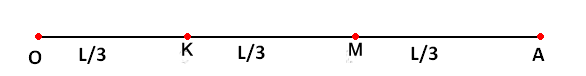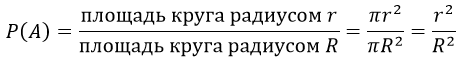Вероятность попадания точек на окружность (3 видео)

Геометрическая вероятность

Цели и задачи: 1) Познакомить учащихся с одним из возможных способов задания

2) Повторение пройденного и закрепление навыков формализации

текстовых вероятностных задач с помощью геометрических фигур.

1) Знать определение геометрической вероятности выбора точки

внутри фигуры на плоскости и прямой;

2) Уметь решать простейшие задачи на геометрическую вероятность,

зная площади фигур или умея их вычислять.

I. Выбор точки из фигуры на плоскости.

Пример 1. Рассмотрим мысленный эксперимент: точку наудачу бросают на квадрат, сторона которого равна 1. Спрашивается, какова вероятность события, которое состоит в том, что расстояние от этой точки до ближайшей стороны квадрата не больше чем ?

В этой задаче речь идет о так называемой геометрической вероятности.

Рассмотрим более общие условия опыта.

Точку наудачу бросают в фигуру F на плоскости. Какова вероятность того, что точка попадает в некоторую фигуру G, которая содержится в фигуре F.

Ответ зависит от того, какой смысл мы вкладываем в выражение «бросить точку наудачу».

Обычно это выражение трактуют так:

1. Брошенная точка может попасть в любую часть фигуры F.

2. Вероятность того, что точка попадает в некоторую фигуру G внутри фигуры F, прямо пропорциональна площади фигуры G.

Подведем итог: пусть и — площади фигур F и G . Вероятность события А «точка Х принадлежит фигуре G, которая содержится в фигуре F», равна

Заметим, что площадь фигуры G не больше, чем площадь фигуры F, поэтому

Вернемся к нашей задаче. Фигура F в этом примере квадрат со стороной 1. Поэтому =1.

Точка удалена от границы квадрата не более чем на , если она попала в заштрихованную на рисунке фигуру G. Чтобы найти площадь , нужно из площади фигуры F вычесть площадь внутреннего квадрата со стороной .

Тогда вероятность того, что точка попала в фигуру G, равна

Пример 2. Из треугольника АВС случайным образом выбирается точка Х. Найти вероятность того, что она принадлежит треугольнику, вершинами которого являются середины сторон треугольника.

Решение: Средние линии треугольника разбивают его на 4 равных треугольников. Значит,

Вероятность того, что точка Х принадлежит треугольнику KMN, равна:

Вывод. Вероятность попадания точки в некоторую фигуру прямо пропорциональна площади этой фигуры.

Задача. Нетерпеливые дуэлянты.

Дуэли в городе Осторожности редко кончаются печальным исходом. Дело в том, что каждый дуэлянт прибывает на место встречи в случайный момент времени между 5 и 6 часами утра и, прождав соперника 5 минут, удаляется. В случае же прибытия последнего в эти 5 минут дуэль состоится. Какая часть дуэлей действительно заканчивается поединком?

Решение: Пусть х и у обозначают время прибытия 1-го т 2-го дуэлянтов соответственно, измеренное в долях часа начиная с 5 часов.

Дуэлянты встречаются, если , т. е. x —

Видео:Теория вероятностей | Математика TutorOnlineСкачать

Геометрическая вероятность

Классическое определение вероятности связано с понятием элементарного события. Рассматривается некий набор Ω равновероятных событий A_i , которые в совокупности дают достоверное событие. И тогда все хорошо: всякое событие разбивается на элементарные, после чего считается его вероятность.

Однако, далеко не всегда исходный набор Ω (т.е. пространство всех элементарных событий) является конечным. Например, в качестве Ω можно взять ограниченное множество точек на плоскости или отрезок на прямой.

В качестве события A можно рассмотреть любую подобласть области Ω. Например, фигуру внутри исходной фигуры на плоскости или отрезок, лежащий внутри исходного отрезка на прямой.

Заметим, что элементарным событием на таком множестве может быть только точка. В самом деле, если множество содержит более одной точки, его можно разбить на два непустых подмножества. Следовательно, такое множество уже неэлементарно.

Теперь определим вероятность. Тут тоже все легко: вероятность «попадания» в каждую конкретную точку равна нулю. Иначе получим бесконечную сумму одинаковых положительных слагаемых (ведь элементарные события равновероятны), которые в сумме по-любому больше P (Ω) = 1.

Итак, элементарные события для бесконечных областей Ω — это отдельные точки, причем вероятность «попадания» в любую из них равна нулю. Но как искать вероятность неэлементарного события, которое, подобно Ω, содержит бесконечное множество точек? Вот мы и пришли к определению геометрической вероятности.

события A , являющегося подмножеством множества Ω точек на прямой или плоскости — это отношение площади фигуры A к площади всего множества Ω:

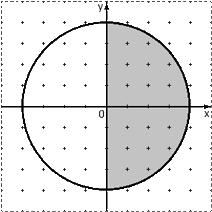
Задача. Мишень имеет форму окружности радиуса 4. Какова вероятность попадания в ее правую половину, если попадание в любую точку мишени равновероятно? При этом промахи мимо мишени исключены.

Взглянем на картинку: нас устроит любая точка из правого полукруга. Очевидно, площадь S ( A ) этого полукруга составляет ровно половину площади всего круга, поэтому имеем:

Как видите, ничего сложного в геометрической вероятности нет. Однако даже в Москве многие репетиторы по высшей математике стараются обойти эту тему стороной, поскольку считают ее необязательной. Результат — непонимание материала и, как следствие, проблемы на экзамене по теории вероятностей.

Чтобы наглядно представить себе, что такое геометрическая вероятность, возьмите лист бумаги и начертите произвольную фигуру. Треугольник, квадрат или окружность — что угодно. Затем возьмите острый, хорошо заточенный карандаш и ткните им в любую точку фигуры. Повторите этот нехитрый процесс несколько раз. Если исключить попадания за пределами фигуры, то получится вот что:

Вероятность попадания в фигуру равна P (Ω) = 1. Это вполне логично, поскольку вся наша фигура — это и есть пространство элементарных событий Ω;
Если некоторую точку (элементарное событие) отметить заранее, то вероятность попадания именно в нее равна нулю. Даже если специально «целиться», точного попадания не будет. Ошибка составит тысячные доли миллиметра, но не ноль;
Теперь возьмем две точки. Вероятность попадания в любую из них все равно ноль. Аналогично, если взять 3 точки. Или пять — без разницы.

Этот опыт показывает, что конечная сумма нулевых слагаемых всегда равна нулю. Но что происходит, когда слагаемых становится бесконечно много? Здесь ситуация не так однозначна, и возможны три варианта:

Сумма равна нулю, как и для конечного набора точек. Если в нашем опыте отмечать точки до бесконечности, вероятность попадания в их объединение все равно нулевая;
Сумма равна некоторому положительному числу — этот случай принципиально отличается от первого. Здесь и возникает геометрическая вероятность;
Сумма равна бесконечности — бывает и такое, но сейчас нас это не интересует.

Почему так происходит? Механизм возникновения положительных чисел и бесконечностей связан с понятием счетности множества. Кроме того, надо понимать, что такое мера Лебега. Впрочем, эти знания действительно нужны вам, только если вы учитесь на математика.

Видео:10 класс, 11 урок, Числовая окружностьСкачать

Геометрическое определение вероятности

Геометрическое определение вероятности применимо для несовместных событий, в которых число равновозможных исходов бесконечно, например, попадания точки на участок отрезка, плоскости, пространства, объёма.

Общая формула для определения геометрической вероятности:

Отношение меры области g, благоприятствующей событию А, к мере всей области G.

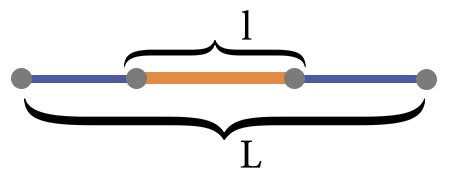
Формула геометрической вероятности попадания точки на участок отрезка L для одномерного пространства равна:

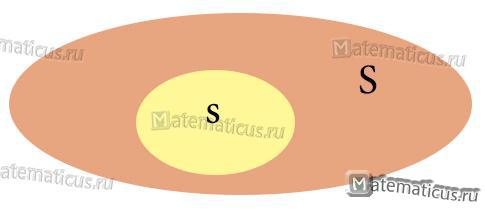
Формула геометрической вероятности попадания точки в область пространства S для фигур в двухмерном пространстве равна:

Формула геометрической вероятности попадания точки в заданный объём для фигур в трёхмерном пространстве V равна:

Пример 1

Решение

Пример 2

Решение

Аналогично первому примеру, вероятность равна:

P(A)=l/L=10/20=1/2

Пример 3

В круг радиуса R помещен меньший круг радиуса r. Найти вероятность того, что точка, наудачу брошенная в большой круг, попадет также и в малый круг. Предполагается, что вероятность попадания точки в круг пропорциональна площади круга и не зависит от его расположения.

Пример 4

Быстро вращающийся диск разделен на четное число равных секторов, попеременно окрашенных в белый и черный цвет. По диску произведен выстрел. Найти вероятность того, что пуля попадет в один из белых секторов. Предполагается, что вероятность попадания пули в плоскую фигуру пропорциональна площади этой фигуры

Решение

P(A)=0.5·πr 2 /πr 2 =0.5

Пример 5

Два студента условились встретиться в определенном месте между 12 и 13 часами дня. Пришедший первым ждет второго в течение 1/4 часа, после чего уходит. Найти вероятность того, что встреча состоится, если каждый студент наудачу выбирает момент своего прихода (в промежутке от 12 до 13 часов).