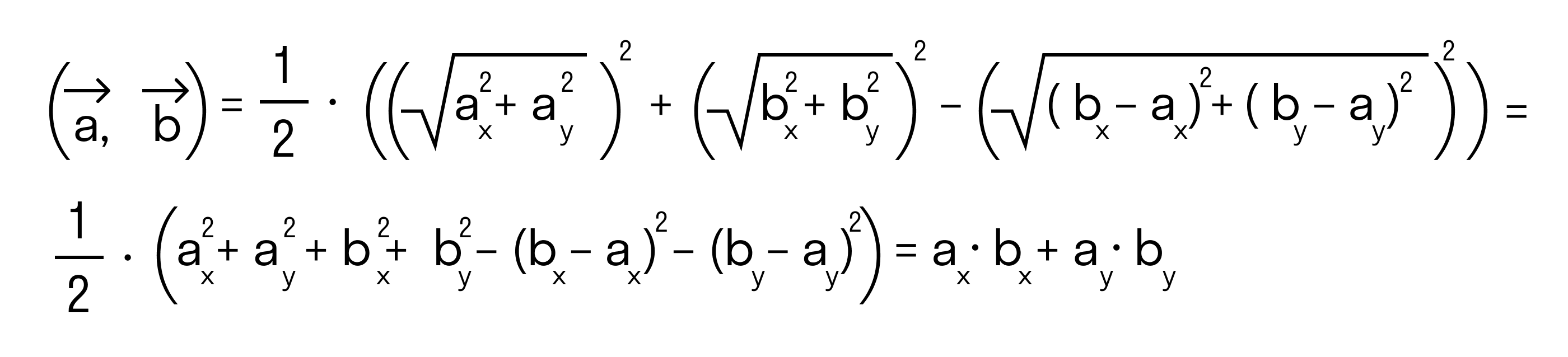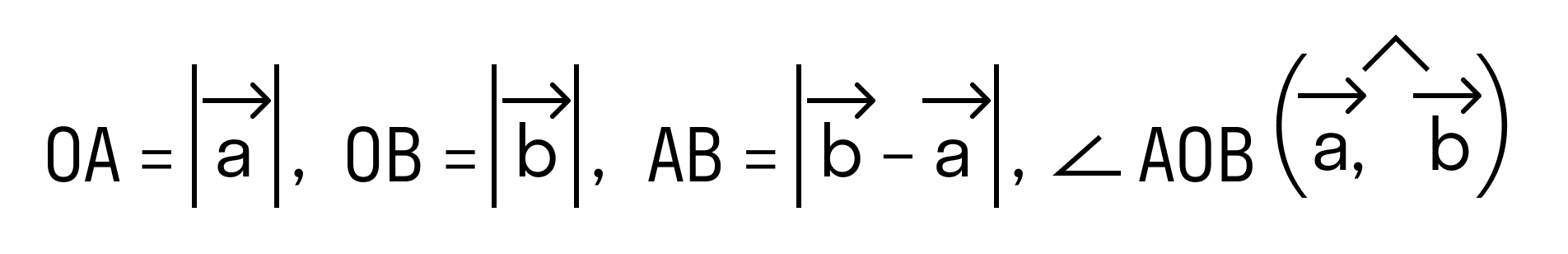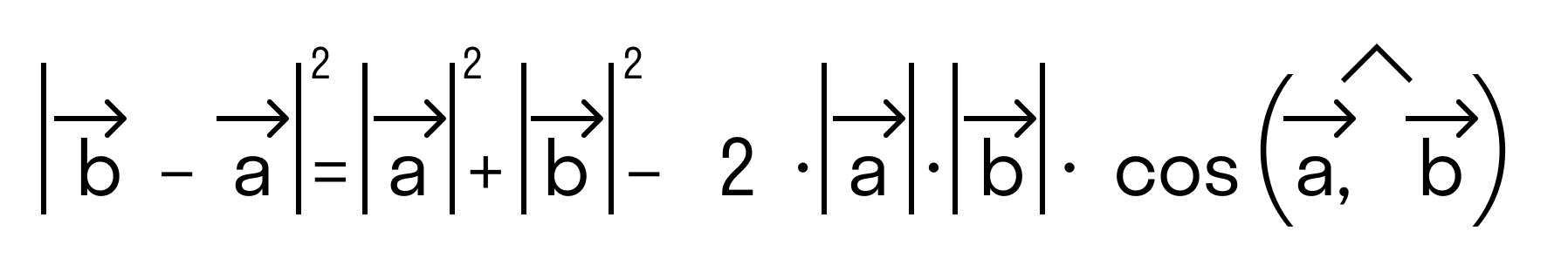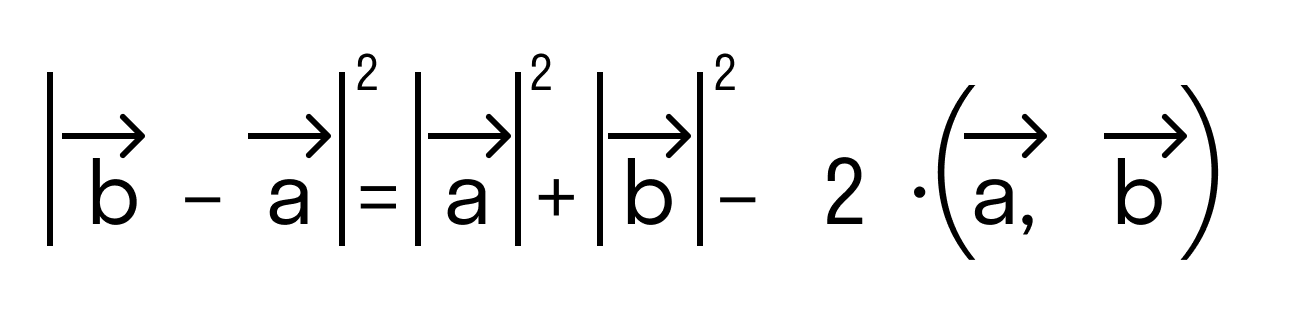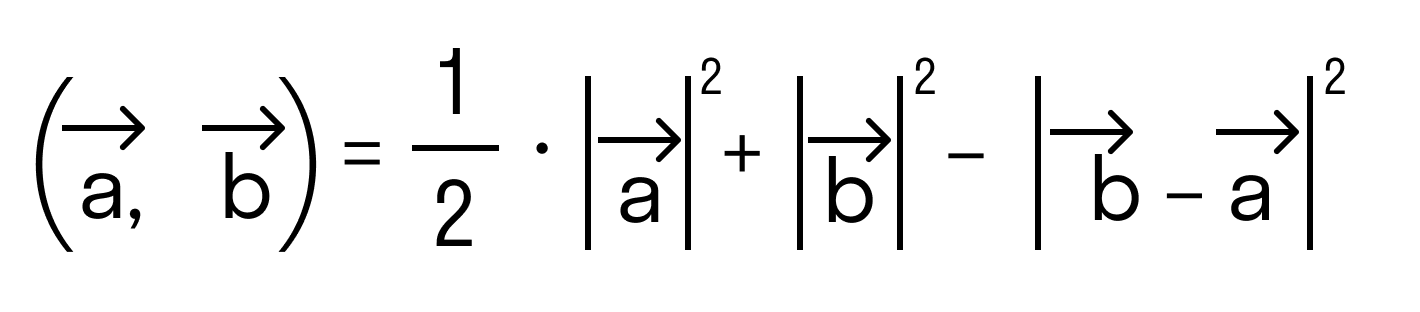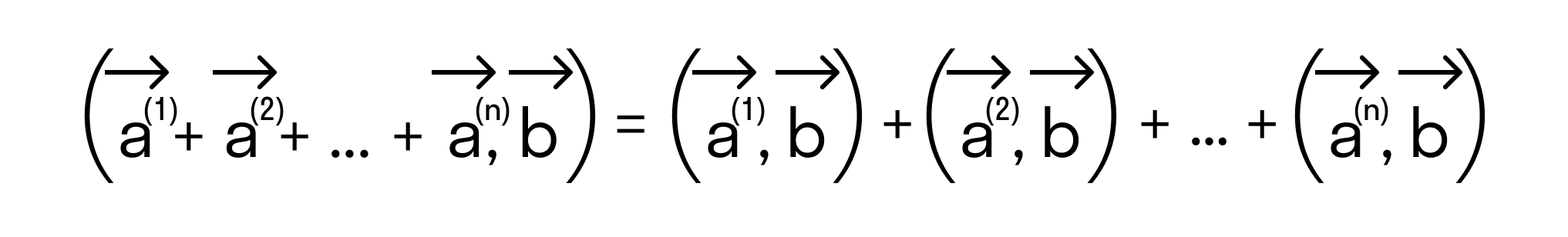Даны вектора oa a ob b (5 видео) | Курс школьной геометрии

Даны вектора oa a ob b

Глава I. Векторы на плоскости и в пространстве

§ 3. Сумма векторов

Пусть даны два вектора а = OA > и b = OB > (рис. 5).

От точки А отложим отрезок АС такой, что AС > = b. Тогда, вектор с = OС > называется суммой векторов а и b и обозначается а + b.

Таким образом, OA > + AС > = OС > . Это равенство называют правилом треугольника сложения двух векторов.

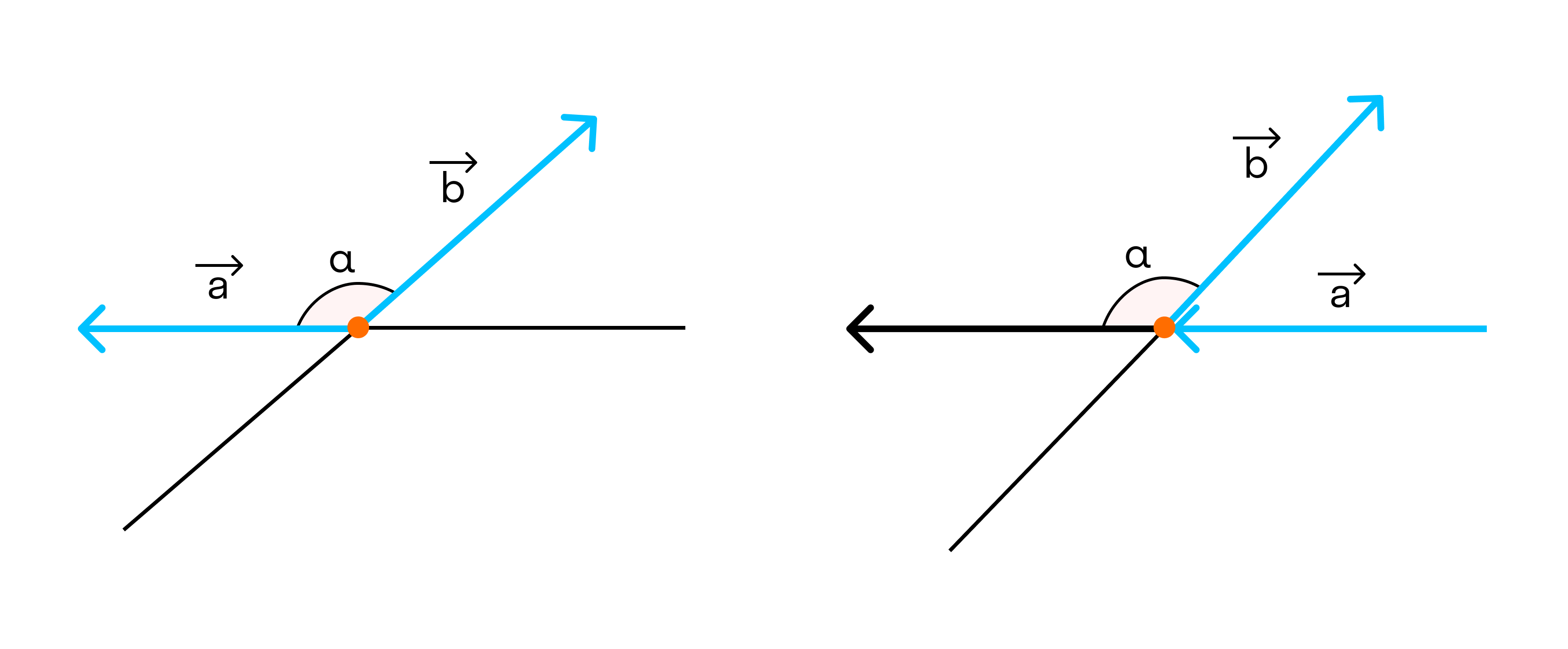
Oчевидно, что это правило справедливо и в том случае, когда точки О, А и В лежат на одной прямой (рис. 6, 7). В частности, а + 0 = а.

Сложение векторов обладает следующими свойствами:

1. Свойство коммутативности (перестановочности): для любых векторов а и b

2. Свойство ассоциативности (сочетательности): для любых векторов а, b и с

1. Пусть a = OA > , b = OB > . Рассмотрим случай, когда точки О, А и В не лежат на одной прямой. На отрезках ОА и ОВ построим параллелограмм ОАСВ (рис. 8).

Тогда |ОА| = |ВС|, (ОА) || (ВС) и |ОВ| = |АС|, (ОВ) || (АС), как противоположные стороны параллелограмма. Следовательно,

что и доказывает равенство (1).

Для случая, когда точки О, А, В лежат на одной прямой, доказательство равенства (1) проведите самостоятельно.

2. От некоторой точки О отложим вектор OA > = а, от точки А отложим вектор AB > = b и, наконец, от точки В отложим вектор BC > = с (рис. 9, 10).

Соединим точки О и С отрезком ОС. Тогда, с одной стороны (см. рис. 9),

и, с другой стороны (см. рис. 10),

что и доказывает равенство (2).

Из риc. 8 видно, что сумма векторов а = OA > и b = OB > равна направленной диагонали OC > параллелограмма ОАСВ, построенного на отрезках ОА и ОВ, т.е.

Это равенство называется правилом параллелограмма сложения двух векторов.

Так как сложение векторов ассоциативно, то сумма трех и большего числа векторов записывается без скобок. Например, вместо (а + b) + с или а + ( b + с ) пишут а + b + с.

Если требуется найти сумму трех или большего числа векторов, то применяют так называемое правило многоугольника. Оно состоит в следующем.

Пусть даны векторы а, b, с, d и требуется найти их сумму.

Выберем некоторую точку О (рис. 11) и построим отрезок ОА такой, что OA > = а,
затем построим отрезок АВ такой, что AB > = b, и т. д.

Построение продолжается до тех пор, пока не будут исчерпаны все векторы-слагаемые. Направленный отрезок OD > , замыкающий полученную ломаную, будет равен сумме данных векторов.

Задача 1. Дан параллелепипед ABCDA₁B₁C₁D₁.
Найти сумму векторов (рис.12).

Из свойств ребер параллелепипеда следует, что

Применив правило многоугольника, получим (рис. 13)

Задача 2. Найти сумму KD > + M C > + DM > + CK >

Применяя свойство коммутативности сложения векторов, получаем

Теперь по правилу многоугольника находим

Задача 3. Дана треугольная пирамида ABCD (рис. 14).
Найти сумму AB > + CD > + AC > + BC > + DA > .

Применив коммутативное и ассоциативное свойства сложения векторов, получим

Содержание

Из точки О выходят два вектора OA =a и OB = b. Найдите какой-нибудь вектор OM, идущий по биссектрисе угла АОВ
Ваш ответ
решение вопроса
Похожие вопросы
Скалярное произведение векторов
Основные определения
Угол между векторами
Скалярное произведение векторов
Скалярное произведение в координатах
Формулы скалярного произведения векторов заданных координатами
Свойства скалярного произведения
Примеры вычислений скалярного произведения
🔍 Видео

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Из точки О выходят два вектора OA =a и OB = b. Найдите какой-нибудь вектор OM, идущий по биссектрисе угла АОВ

Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Ваш ответ

Видео:Даны векторы a(1; 2), b( −3; 6) и c(4; -2). Найдите длину вектора a- b + с.Скачать

решение вопроса

Видео:Математика без Ху!ни. Смешанное произведение векторовСкачать

Скалярное произведение векторов

О чем эта статья:

11 класс, ЕГЭ/ОГЭ

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Видео:Выразить векторы. Разложить векторы. Задачи по рисункам. ГеометрияСкачать

Основные определения

Система координат — способ определить положение и перемещение точки или тела с помощью чисел или других символов.

Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Как найти координаты точки мы рассказали в этой статье.

Скаляр — это величина, которая полностью определяется в любой координатной системе одним числом или функцией.

Вектор — направленный отрезок прямой, для которого указано, какая точка является началом, а какая — концом.

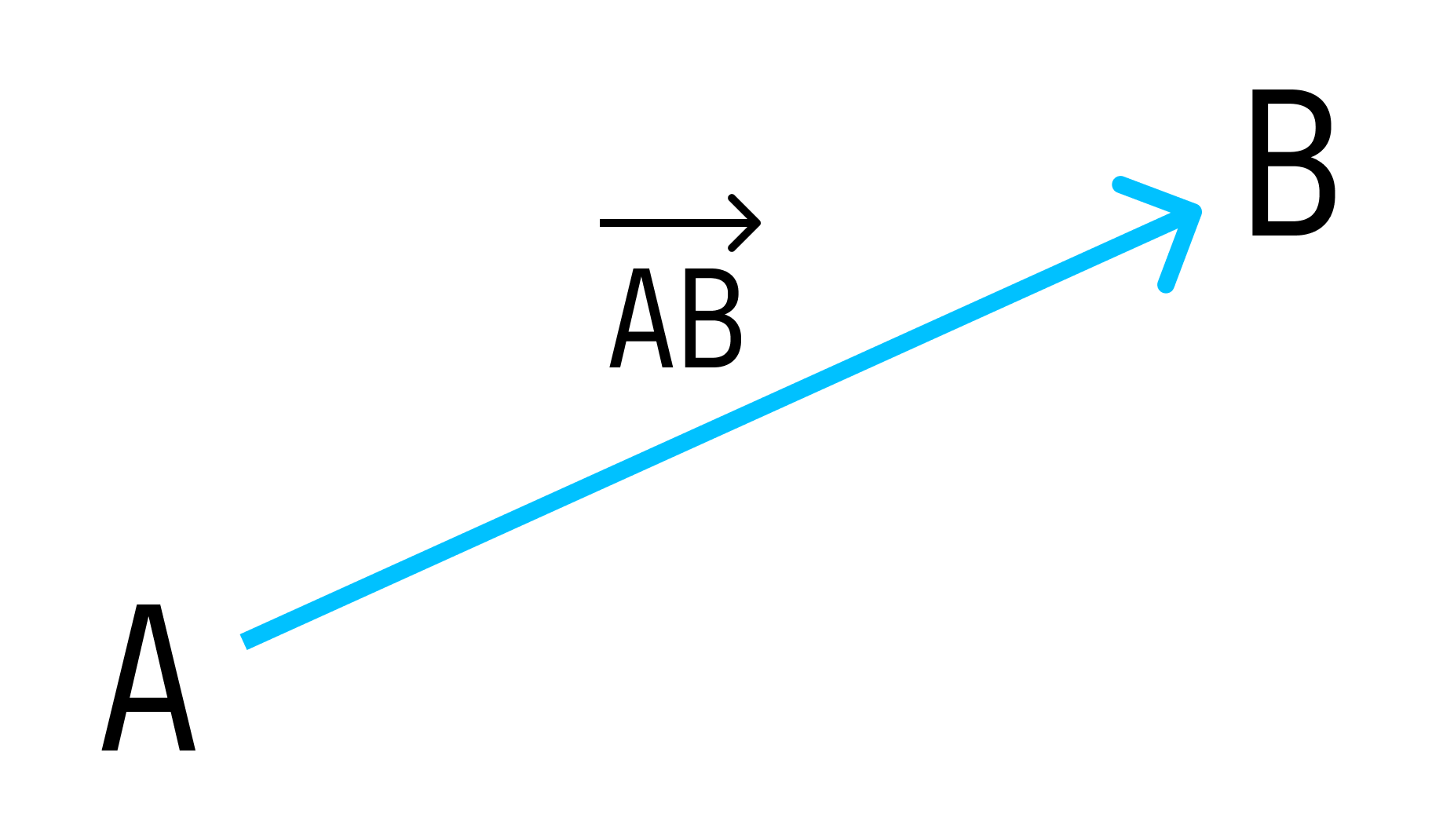
Вектор с началом в точке A и концом в точке B принято обозначать как →AB. Векторы также можно обозначать малыми латинскими буквами со стрелкой или черточкой над ними, вот так: →a.

Скалярное произведение — это операция над двумя векторами, результатом которой является скаляр, то есть число, которое не зависит от выбора системы координат.

Результат операции является число. То есть при умножении вектор на вектор получается число. Если длины векторов |→a|, |→b| — это числа, косинус угла — число, то их произведение |→a|*|→b|*cos∠(→a, →b) тоже будет числом.

Чтобы разобраться в теме этой статьи, нам еще нужно узнать особенности угла между векторами.

Видео:Компланарны ли векторы: a=(2;5;8), b=(1;-3;-7) и c=(0;5;10)?Скачать

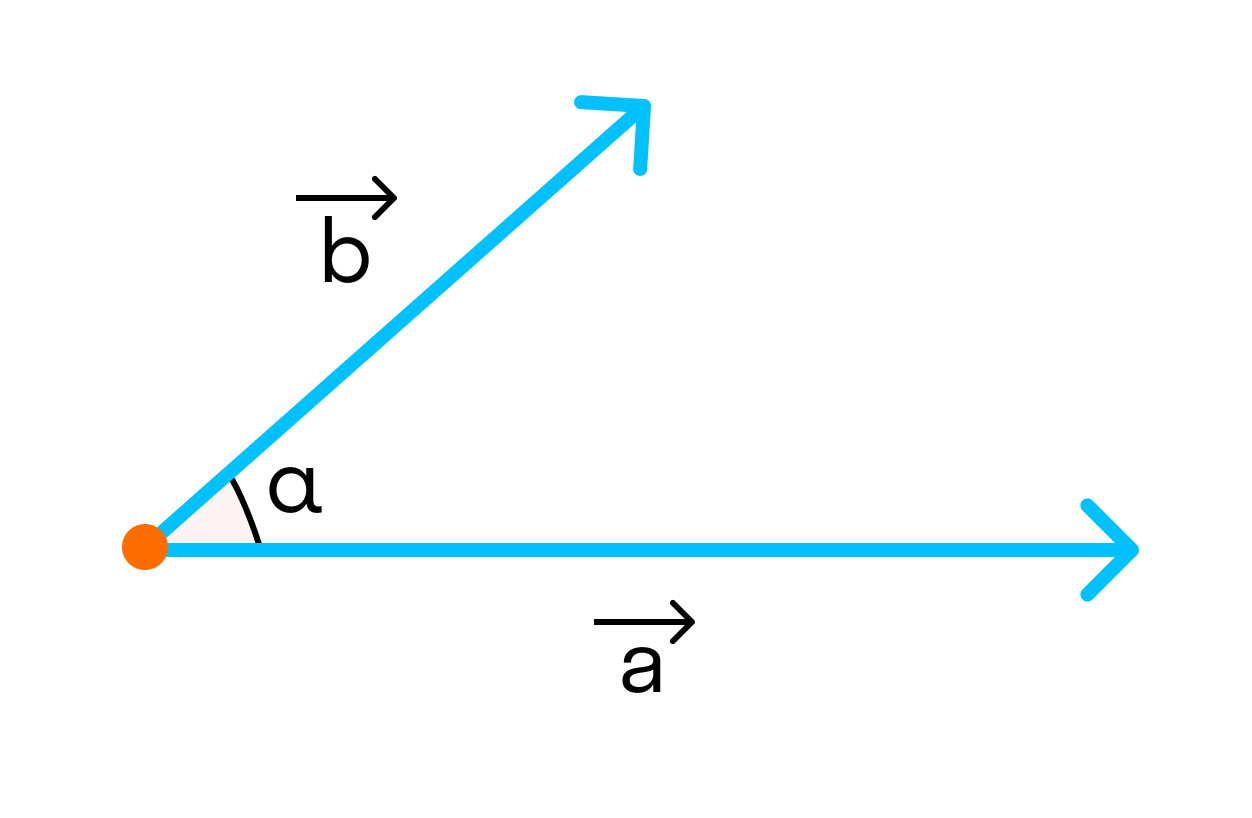
Угол между векторами

Угол между векторами ∠(→a, →b) может принимать значения от 0° до 180° градусов включительно. Аналитически это можно записать в виде двойного неравенства: 0°=

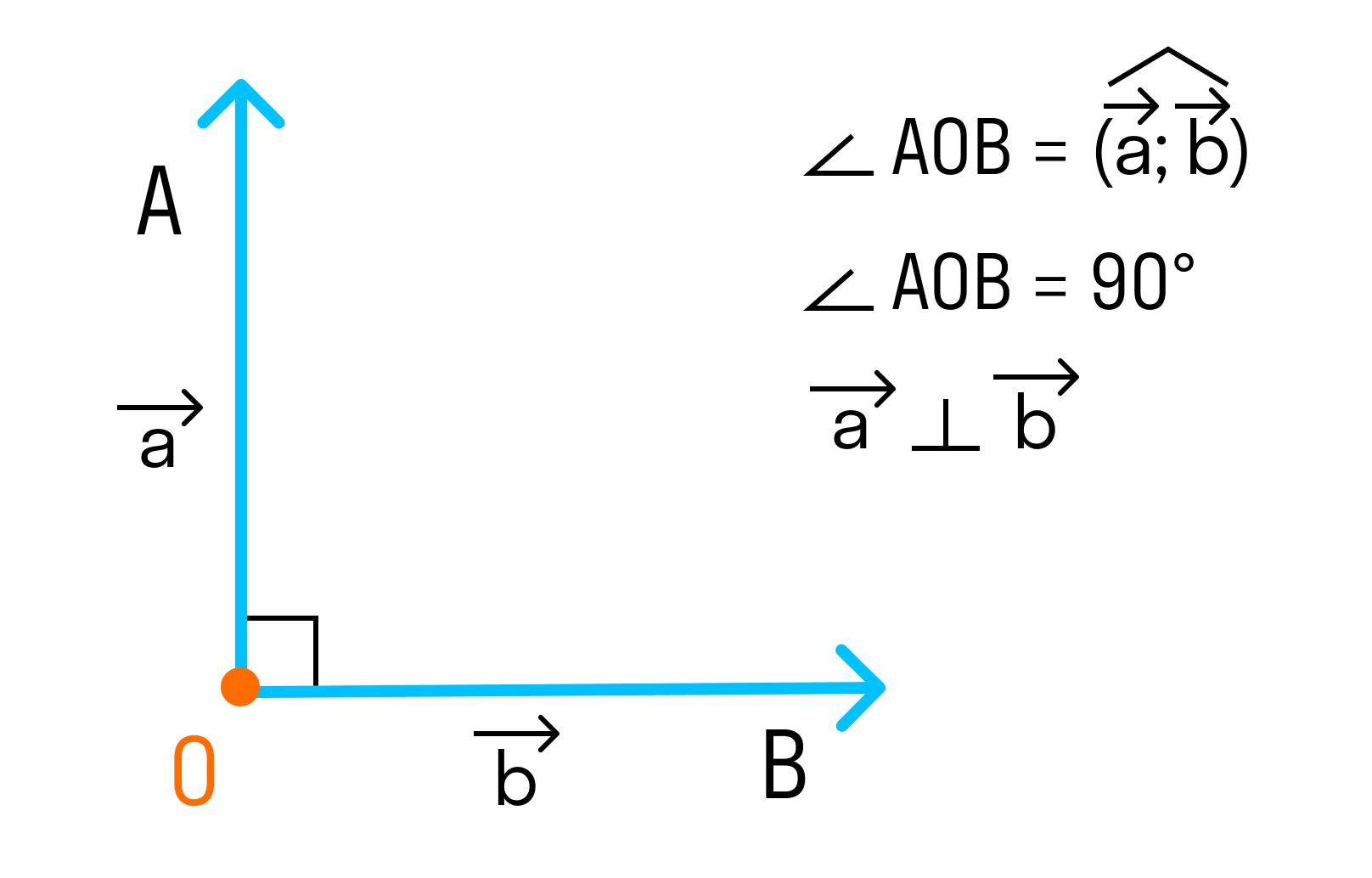
2. Если угол между векторами равен 90°, то такие векторы перпендикулярны друг другу.

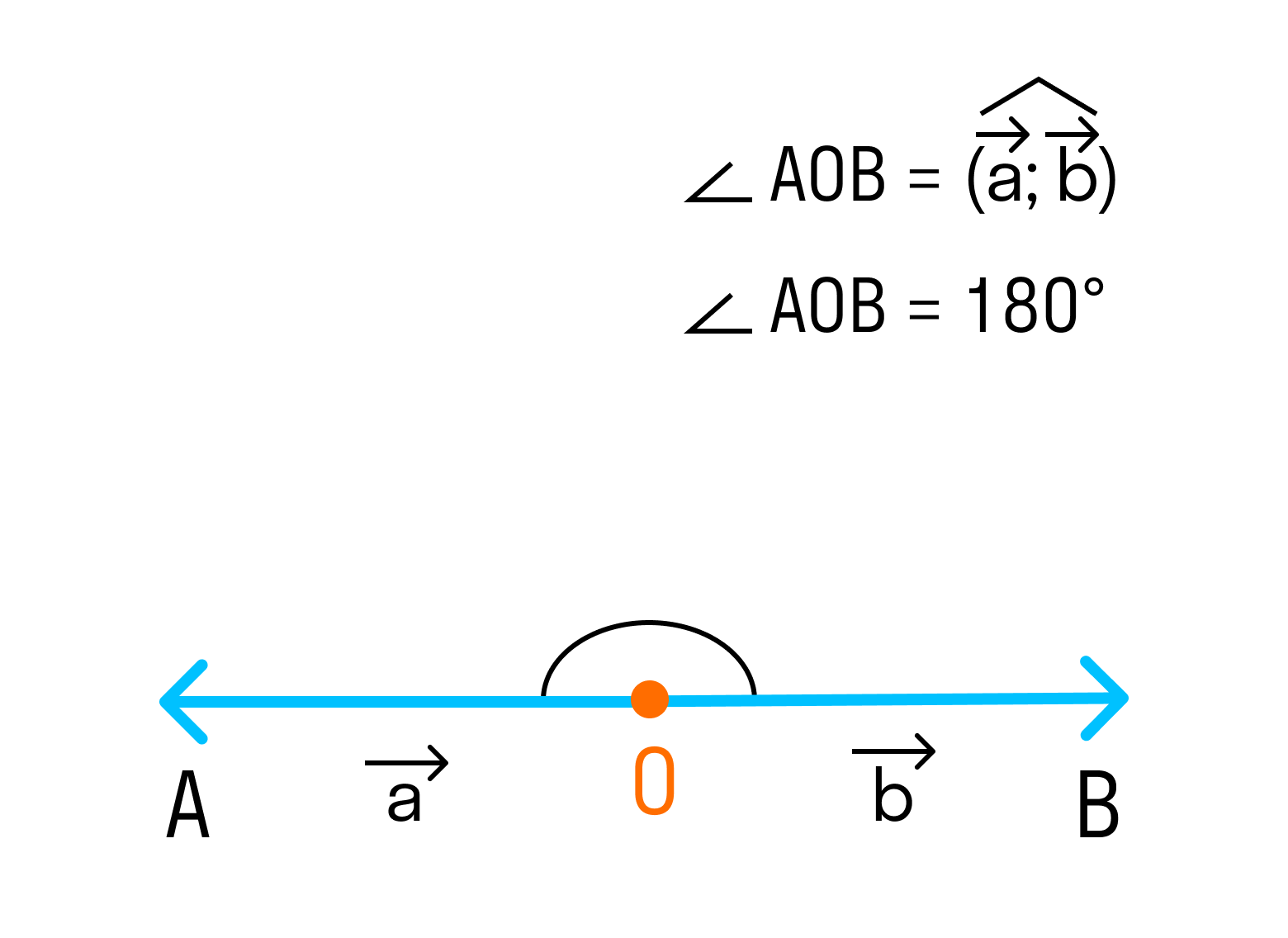
3. Если векторы направлены в разные стороны, тогда угол между ними 180°.

Также векторы могут образовывать тупой угол. Это выглядит так:

Видео:Скалярное произведение векторов. 9 класс.Скачать

Скалярное произведение векторов

Определение скалярного произведения можно сформулировать двумя способами:

Скалярное произведение двух векторов a и b дает в результате скалярную величину, которая равна сумме попарного произведения координат векторов a и b.

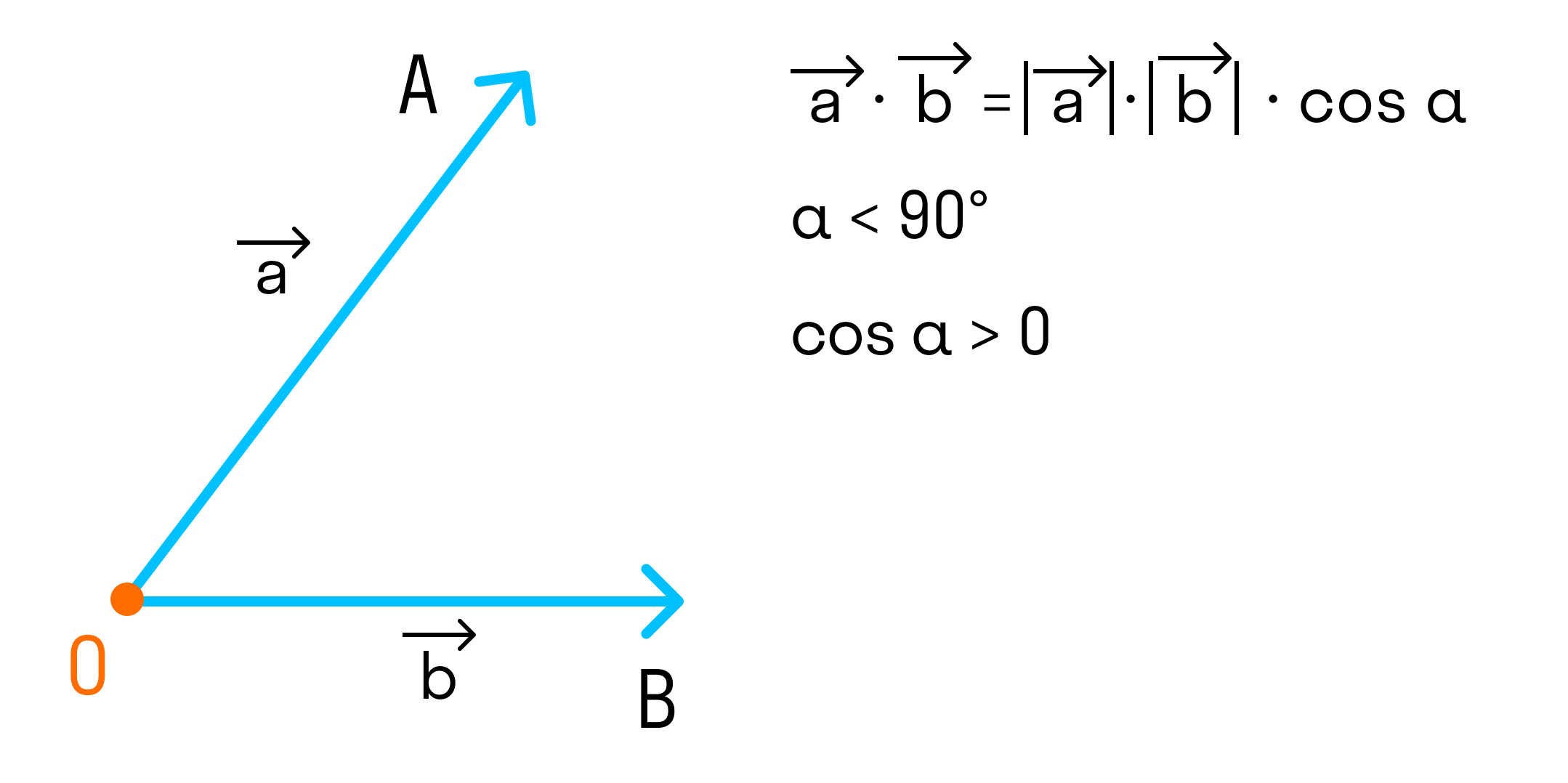
Скалярным произведением двух векторов a и b будет скалярная величина, равная произведению модулей этих векторов, умноженная на косинус угла между ними:

→a * →b = →|a| * →|b| * cosα

Алгебраическая интерпретация.

Что важно запомнить про геометрическую интерпретацию скалярного произведения:

Если угол между векторами острый и векторы ненулевые, то скалярное произведение положительно, то есть cosα > 0.
Если угол между векторами тупой и векторы ненулевые, то скалярное произведение отрицательно, так как cosα

Видео:Полный разбор задач с векторами №2 ЕГЭ ПРОФИЛЬ 2024 | Профильная математика ЕГЭ 2024 | УМСКУЛСкачать

Скалярное произведение в координатах

Вычисление скалярного произведения можно произвести через координаты векторов в заданной плоскости или в пространстве.

Скалярным произведением двух векторов на плоскости или в трехмерном пространстве в прямоугольной системе координат называется сумма произведений соответствующих координат векторов →a и →b.

То есть для векторов →a = (ax, ay), →b = (bx, by) на плоскости в прямоугольной декартовой системе координат формула для вычисления скалярного произведения имеет вид: (→a, →b) = ax*bx + ay*by

А для векторов →a = (ax, ay, az), →b = (bx, by, bz) в трехмерном пространстве скалярное произведение в координатах находится так: (→a, →b) = ax*bx + ay*by + az*bz

Докажем это определение:

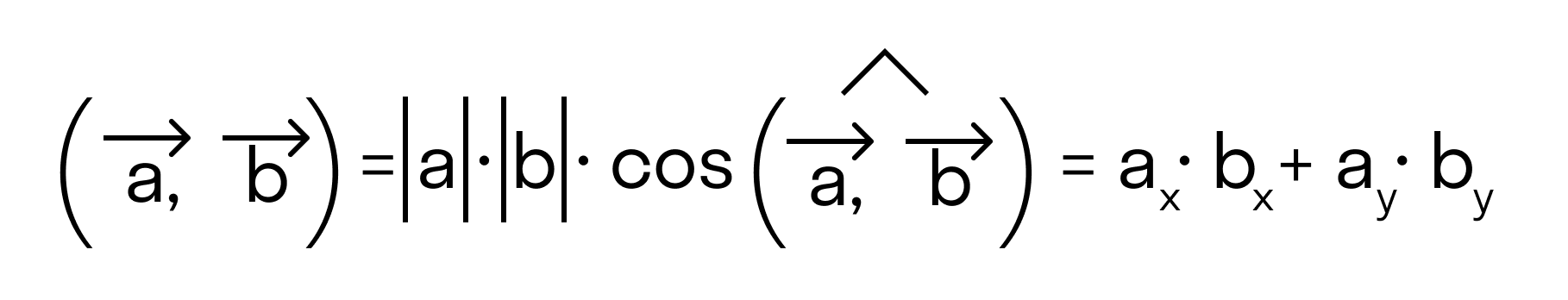
для векторов →a = (ax, ay), →b = (bx, by) на плоскости, заданных в прямоугольной декартовой системе координат.

Отложим от начала координат (точка О) векторы →OB = →b = (bx, by) и →OA = →a = (ax, ay)

Тогда, →AB = →OB — →OA = →b — →a = (bx — ax, by — ay)

Будем считать точки О, А и В вершинами треугольника ОАВ. По теореме косинусов можно записать:

то последнее равенство можно переписать так:

а по первому определению скалярного произведения имеем

Вспомнив формулу вычисления длины вектора по координатам, получаем

Абсолютно аналогично доказывается справедливость равенств (→a, →b) = |→a|*|→b|*cos(→a, →b) = ax*bx + ay*by + ax*bz для векторов →a = (ax, ay, az), →b = (bx, by, bz), заданных в прямоугольной системе координат трехмерного пространства.

Формула скалярного произведения векторов в координатах позволяет заключить, что скалярный квадрат вектора равен сумме квадратов всех его координат: на плоскости (→a, →a) = ax2 + ay2 в пространстве (→a, →a) = ax2 + ay2 + az2.

Записывайтесь на наши курсы по математике для учеников с 1 по 11 классы!

Видео:Понятие вектора. Коллинеарные вектора. 9 класс.Скачать

Формулы скалярного произведения векторов заданных координатами

Формула скалярного произведения векторов для плоских задач

В плоской задаче скалярное произведение векторов a = и b = можно найти по формуле:

a * b = ax * bx + ay * by

Формула скалярного произведения векторов для пространственных задач

В пространственной задаче скалярное произведение векторов a = и b = можно найти по формуле:

a * b = ax * bx + ay * by + az * bz

Формула скалярного произведения n-мерных векторов

В n-мерном пространстве скалярное произведение векторов a = и b = можно найти по формуле:

a * b = a1 * b1 + a2 * b2 + . + an * bn

Видео:№411. Даны векторы а{ — 1; 1; 1}, b{0; 2; —2}, с { — 3; 2; 0} и d{ — 2; 1; —2}. Найдите координатыСкачать

Свойства скалярного произведения

Свойства скалярного произведения векторов:

→0 * →0 = 0

Скалярное произведение вектора самого на себя равно квадрату его модуля:

→a * →a = →∣∣a∣∣2

Операция скалярного произведения коммуникативна, то есть соответствует переместительному закону:

→a * →b = →b * →a

Операция скалярного умножения дистрибутивна, то есть соответствует распределительному закону:

(→a + →b) * →c = →a * →c + →b * →c

Сочетательный закон для скалярного произведения:

(k * →a) * →b = k * (→a * →b)

Если скалярное произведение двух ненулевых векторов равно нулю, то эти векторы ортогональны, то есть перпендикулярны друг другу:

a ≠ 0, b ≠ 0, a * b = 0 a ┴ b

Эти свойства очень легко обосновать, если отталкиваться от определения скалярного произведения в координатной форме и от свойств операций сложения и умножения действительных чисел.

Для примера докажем свойство коммутативности скалярного произведения (→a, →b) = (→b, →a)

По определению (→a, →b) = ax*bx + ay*by и (→b, →a) = bx*ax + by*ay. В силу свойства коммутативности операции умножения действительных чисел, справедливо ax*bx = bx*ax b ay*by = by*ay, тогда ax*bx + ay*by = bx*ax + by*ay.

Следовательно, (→a, →b) = (→b, →a), что и требовалось доказать.

Аналогично доказываются остальные свойства скалярного произведения.

Следует отметить, что свойство дистрибутивности скалярного произведения справедливо для любого числа слагаемых, то есть,

Видео:#вектор Разложение вектора по ортам. Направляющие косинусыСкачать

Примеры вычислений скалярного произведения

Пример 1.

Вычислите скалярное произведение двух векторов →a и →b, если их длины равны 3 и 7 единиц соответственно, а угол между ними равен 60 градусам.

У нас есть все данные, чтобы вычислить скалярное произведение по определению:

(→a,→b) = →|a| * →|b| * cos(→a,→b) = 3 * 7 cos60° = 3 * 7 * 1/2 = 21/2 = 10,5.

Ответ: (→a,→b) = 21/2 = 10,5.

Пример 2.

Найти скалярное произведение векторов →a и →b, если →|a| = 2, →|b| = 5, ∠(→a,→b) = π/6.

Используем формулу →a * →b = →|a| * →|b| * cosα.

В данном случае:

→a * →b = →|a| * →|b| * cosα = 2 * 5 * cosπ/6 = 10 * √3/2 = 5√3

Пример 3.

Как найти скалярное произведение векторов →a = 7*→m + 3*→n и →b = 5*→m + 8*→n, если векторы →m и →n перпендикулярны и их длины равны 3 и 2 единицы соответственно.

По свойству дистрибутивности скалярного произведения имеем

Сочетательное свойство позволяет нам вынести коэффициенты за знак скалярного произведения:

В силу свойства коммутативности последнее выражение примет вид

Итак, после применения свойств скалярного произведения имеем

Осталось применить формулу для вычисления скалярного произведения через длины векторов и косинус угла между ними:

Пример 4.

В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, найти косинус угла между прямыми AB1 и BC1.

Если сделать выносной рисунок основания призмы, получим понятный плоскостной рисунок с помощью которого можно легко найти координаты всех интересующих точек.

Точка А имеет координаты (0;0;0). Точка С — (1;0;0). Точка В — (1/2;√3/2;0). Тогда точка В1 имеет координаты (1/2;√3/2;1), а точка С1 – (1;0;1).

Найдем координаты векторов →AB1 и →BC1:

Найдем длины векторов →AB1 и →BC1:

Найдем скалярное произведение векторов →AB1 и →BC1:

Найдем косинус угла между прямыми AB1 и BC1:

Пример 5.

а) Проверить ортогональность векторов: →a(1; 2; -4) и →b(6; -1; 1) .

б) Выяснить, будут ли перпендикулярными отрезки KL и MN, если K(3;5), L(-2;0), M(8;-1), N(1;4).

а) Выясним, будут ли ортогональны пространственные векторы. Вычислим их скалярное произведение: →ab = 1*6 + 2*(-1) + (-4)*1 = 0, следовательно

б) Здесь речь идёт об обычных отрезках плоскости, а задача всё равно решается через векторы. Найдем их: →KL(-2-3; 0-5) = →KL(-5; -5), →MN(1-8; 4-(-1)) = →MN(-7;5)

Вычислим их скалярное произведение: →KL*→MN = -5*(-7) + (-5)*5 = 10 ≠ 0, значит, отрезки KL и MN не перпендикулярны.

Обратите внимание на два существенных момента:

В данном случае нас не интересует конкретное значение скалярного произведения, важно, что оно не равно нулю.
В окончательном выводе подразумевается, что если векторы не ортогональны, значит, соответствующие отрезки тоже не будут перпендикулярными. Геометрически это очевидно, поэтому можно сразу записывать вывод об отрезках, что они не перпендикулярны.

Ответ: а) →a перпендикулярно →b, б) отрезки KL, MN не перпендикулярны.

Пример 6.

Даны три вершины треугольника A(-1; 0), B(3; 2), C(5; -4). Найти угол при вершине B — ∠ABC.

По условию чертеж выполнять не требуется, но для удобства можно сделать:

Требуемый угол ∠ABC помечен зеленой дугой. Сразу вспоминаем школьное обозначение угла: ∠ABC — особое внимание на среднюю букву B — это и есть нужная нам вершина угла. Для краткости можно также записать просто ∠B.

Из чертежа видно, что угол ∠ABC треугольника совпадает с углом между векторами →BA и →BC, иными словами: ∠ABC = ∠(→BA; →BC).

Вычислим скалярное произведение:

Вычислим длины векторов:

Найдем косинус угла:

Когда такие примеры не будут вызывать трудностей, можно начать записывать вычисления в одну строчку:

Полученное значение не является окончательным, поэтому нет особого смысла избавляться от иррациональности в знаменателе.

Найдём сам угол:

Если посмотреть на чертеж, то результат действительно похож на правду. Для проверки угол также можно измерить и транспортиром.

Ответ: ∠ABC = arccos(1/5√2) ≈1,43 рад. ≈ 82°

Важно не перепутать, что в задаче спрашивалось про угол треугольника, а не про угол между векторами. Поэтому указываем точный ответ: arccos(1/5√2) и приближенное значение угла: ≈1,43 рад. ≈ 82°, которое легко найти с помощью калькулятора.

А те, кому мало и хочется еще порешать, могут вычислить углы ∠A, ∠C, и убедиться в справедливости канонического равенства ∠A + ∠B + ∠C = 180°.