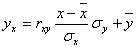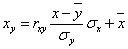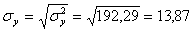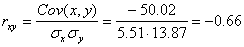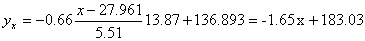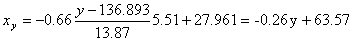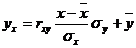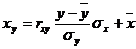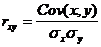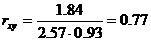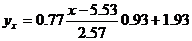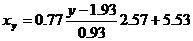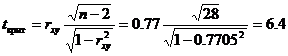Пример 1 . По данной корреляционной таблице построить прямые регрессии с X на Y и с Y на X . Найти соответствующие коэффициенты регрессии и коэффициент корреляции между X и Y .
| y/x | 15 | 20 | 25 | 30 | 35 | 40 |
| 100 | 2 | 2 | ||||
| 120 | 4 | 3 | 10 | 3 | ||
| 140 | 2 | 50 | 7 | 10 | ||
| 160 | 1 | 4 | 3 | |||
| 180 | 1 | 1 |
Решение:
Уравнение линейной регрессии с y на x будем искать по формуле
а уравнение регрессии с x на y, использовав формулу:
где x x , y — выборочные средние величин x и y, σx, σy — выборочные среднеквадратические отклонения.
Находим выборочные средние:
x = (15(1 + 1) + 20(2 + 4 + 1) + 25(4 + 50) + 30(3 + 7 + 3) + 35(2 + 10 + 10) + 40(2 + 3))/103 = 27.961
y = (100(2 + 2) + 120(4 + 3 + 10 + 3) + 140(2 + 50 + 7 + 10) + 160(1 + 4 + 3) + 180(1 + 1))/103 = 136.893
Выборочные дисперсии:
σ 2 x = (15 2 (1 + 1) + 20 2 (2 + 4 + 1) + 25 2 (4 + 50) + 30 2 (3 + 7 + 3) + 35 2 (2 + 10 + 10) + 40 2 (2 + 3))/103 — 27.961 2 = 30.31
σ 2 y = (100 2 (2 + 2) + 120 2 (4 + 3 + 10 + 3) + 140 2 (2 + 50 + 7 + 10) + 160 2 (1 + 4 + 3) + 180 2 (1 + 1))/103 — 136.893 2 = 192.29
Откуда получаем среднеквадратические отклонения:
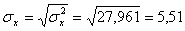
Определим коэффициент корреляции:
где ковариация равна:
Cov(x,y) = (35•100•2 + 40•100•2 + 25•120•4 + 30•120•3 + 35•120•10 + 40•120•3 + 20•140•2 + 25•140•50 + 30•140•7 + 35•140•10 + 15•160•1 + 20•160•4 + 30•160•3 + 15•180•1 + 20•180•1)/103 — 27.961 • 136.893 = -50.02
Запишем уравнение линий регрессии y(x):
и уравнение x(y):
Построим найденные уравнения регрессии на чертеже, из которого сделаем следующие вывод:
1) обе линии проходят через точку с координатами (27.961; 136.893)
2) все точки расположены близко к линиям регрессии.
Пример 2 . По данным корреляционной таблицы найти условные средние y и x . Оценить тесноту линейной связи между признаками x и y и составить уравнения линейной регрессии y по x и x по y . Сделать чертеж, нанеся его на него условные средние и найденные прямые регрессии. Оценить силу связи между признаками с помощью корреляционного отношения.
Корреляционная таблица:
| X / Y | 2 | 4 | 6 | 8 | 10 |
| 1 | 5 | 4 | 2 | 0 | 0 |
| 2 | 0 | 6 | 3 | 3 | 0 |
| 3 | 0 | 0 | 1 | 2 | 3 |
| 5 | 0 | 0 | 0 | 0 | 1 |
Уравнение линейной регрессии с y на x имеет вид:
Уравнение линейной регрессии с x на y имеет вид:
найдем необходимые числовые характеристики.
Выборочные средние:
x = (2(5) + 4(4 + 6) + 6(2 + 3 + 1) + 8(3 + 2) + 10(3 + 1) + )/30 = 5.53
y = (2(5) + 4(4 + 6) + 6(2 + 3 + 1) + 8(3 + 2) + 10(3 + 1) + )/30 = 1.93
Дисперсии:
σ 2 x = (2 2 (5) + 4 2 (4 + 6) + 6 2 (2 + 3 + 1) + 8 2 (3 + 2) + 10 2 (3 + 1))/30 — 5.53 2 = 6.58
σ 2 y = (1 2 (5 + 4 + 2) + 2 2 (6 + 3 + 3) + 3 2 (1 + 2 + 3) + 5 2 (1))/30 — 1.93 2 = 0.86
Откуда получаем среднеквадратические отклонения:
σx = 2.57 и σy = 0.93
и ковариация:
Cov(x,y) = (2•1•5 + 4•1•4 + 6•1•2 + 4•2•6 + 6•2•3 + 8•2•3 + 6•3•1 + 8•3•2 + 10•3•3 + 10•5•1)/30 — 5.53 • 1.93 = 1.84
Определим коэффициент корреляции:
Запишем уравнения линий регрессии y(x):
и вычисляя, получаем:
yx = 0.28 x + 0.39
Запишем уравнения линий регрессии x(y):
и вычисляя, получаем:
xy = 2.13 y + 1.42
Если построить точки, определяемые таблицей и линии регрессии, увидим, что обе линии проходят через точку с координатами (5.53; 1.93) и точки расположены близко к линиям регрессии.
Значимость коэффициента корреляции.
По таблице Стьюдента с уровнем значимости α=0.05 и степенями свободы k=30-m-1 = 28 находим tкрит:
tкрит (n-m-1;α/2) = (28;0.025) = 2.048
где m = 1 — количество объясняющих переменных.
Если tнабл > tкритич, то полученное значение коэффициента корреляции признается значимым (нулевая гипотеза, утверждающая равенство нулю коэффициента корреляции, отвергается).
Поскольку tнабл > tкрит, то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициент корреляции статистически — значим.
Пример 3 . Распределение 50 предприятий пищевой промышленности по степени автоматизации производства Х (%) и росту производительности труда Y (%) представлено в таблице. Необходимо:
1. Вычислить групповые средние i и j x y, построить эмпирические линии регрессии.
2. Предполагая, что между переменными Х и Y существует линейная корреляционная зависимость:
а) найти уравнения прямых регрессии, построить их графики на одном чертеже с эмпирическими линиями регрессии и дать экономическую интерпретацию полученных уравнений;
б) вычислить коэффициент корреляции; на уровне значимости α= 0,05 оценить его значимость и сделать вывод о тесноте и направлении связи между переменными Х и Y;
в) используя соответствующее уравнение регрессии, оценить рост производительности труда при степени автоматизации производства 43%.
Скачать решение
Пример . По корреляционной таблице рассчитать ковариацию и коэффициент корреляции, построить прямые регрессии.
Пример 4 . Найти выборочное уравнение прямой Y регрессии Y на X по данной корреляционной таблице.
Решение находим с помощью калькулятора.
Скачать
Пример №4
Пример 5 . С целью анализа взаимного влияния прибыли предприятия и его издержек выборочно были проведены наблюдения за этими показателями в течение ряда месяцев: X — величина месячной прибыли в тыс. руб., Y — месячные издержки в процентах к объему продаж.
Результаты выборки сгруппированы и представлены в виде корреляционной таблицы, где указаны значения признаков X и Y и количество месяцев, за которые наблюдались соответствующие пары значений названных признаков.
Решение.
Пример №5
Пример №6
Пример №7
Пример 6 . Данные наблюдений над двумерной случайной величиной (X, Y) представлены в корреляционной таблице. Методом наименьших квадратов найти выборочное уравнение прямой регрессии Y на X. Построить график уравнения регрессии и показать точки (x;y)б рассчитанные по таблице данных.
Решение.
Скачать решение
Пример 7 . Дана корреляционная таблица для величин X и Y, X- срок службы колеса вагона в годах, а Y — усредненное значение износа по толщине обода колеса в миллиметрах. Определить коэффициент корреляции и уравнения регрессий.
| X / Y | 0 | 2 | 7 | 12 | 17 | 22 | 27 | 32 | 37 | 42 |
| 0 | 3 | 6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 25 | 108 | 44 | 8 | 2 | 0 | 0 | 0 | 0 | 0 |
| 2 | 30 | 50 | 60 | 21 | 5 | 5 | 0 | 0 | 0 | 0 |
| 3 | 1 | 11 | 33 | 32 | 13 | 2 | 3 | 1 | 0 | 0 |
| 4 | 0 | 5 | 5 | 13 | 13 | 7 | 2 | 0 | 0 | 0 |
| 5 | 0 | 0 | 1 | 2 | 12 | 6 | 3 | 2 | 1 | 0 |
| 6 | 0 | 1 | 0 | 1 | 0 | 0 | 2 | 1 | 0 | 1 |
| 7 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 |
Решение.
Скачать решение
Пример 8 . По заданной корреляционной таблице определить групповые средние количественных признаков X и Y. Построить эмпирические и теоретические линии регрессии. Предполагая, что между переменными X и Y существует линейная зависимость:
- Вычислить выборочный коэффициент корреляции и проанализировать степень тесноты и направления связи между переменными.
- Определить линии регрессии и построить их графики.
Скачать
Видео:Ковариационная матрицаСкачать

Ковариационная и корреляционная матрицы случайного вектора
В случае многомерной случайной величины (случайного вектора) характеристикой разброса ее составляющих и связей между ними является ковариационная матрица.
Ковариационная матрица определяется как математическое ожидание произведения центрированного случайного вектора на тот же, но транспонированный вектор:
где
Ковариационная матрица имеет вид
где по диагонали стоят дисперсии координат случайного вектора on=DXi, o22=DX2, окк = DXk, а остальные элементы представляют собой ковариации между координатами
Ковариационная матрица является симметрической матрицей, т.е.
Для примера рассмотрим ковариационную матрицу двумерного вектора
Аналогично получается ковариационная матрица для любого /^-мерного вектора.
Дисперсии координат можно представить в виде
где Gi,C2. 0? — средние квадратичные отклонения координат случайного вектора.
Коэффициентом корреляции называется, как известно, отношение ковариации к произведению средних квадратичных отклонений:
После нормирования по последнему соотношению членов ковариационной матрицы получают корреляционную матрицу
которая является симметрической и неотрицательно определенной.
Многомерным аналогом дисперсии случайной величины является обобщенная дисперсия, под которой понимается величина определителя ковариационной матрицы
Другой общей характеристикой степени разброса многомерной случайной величины является след ковариационной матрицы
где т — вектор-столбец математических ожиданий;
|Х| — определитель ковариационной матрицы X;
? -1 — обратная ковариационная матрица.
Матрица X -1 , обратная к матрице X размерности пх п, может быть получена различными способами. Одним из них является метод Жордана—Гаусса. В этом случае составляется матричное уравнение
где х — вектор-столбец переменных, число которых равно я; b — я-мерный вектор-столбец правых частей.
Умножим слева уравнение (6.21) на обратную матрицу ХГ 1 :
Так как произведение обратной матрицы на данную дает единичную матрицу Е, то
Если вместо b взять единичный вектор
то произведение X -1 -ех дает первый столбец обратной матрицы. Если же взять второй единичный вектор
то произведение Е 1 е2 дает первый столбец обратной матрицы и т.д. Таким образом, последовательно решая уравнения
методом Жордана—Гаусса, получаем все столбцы обратной матрицы.
Другой метод получения матрицы, обратной к матрице Е, связан с вычислением алгебраических дополнений AtJ.= (/= 1, 2. п; j = 1, 2, . п) к элементам данной матрицы Е, подстановкой их вместо элементов матрицы Е и транспортированием такой матрицы:
Обратная матрица получается после деления элементов В на определитель матрицы Е:
Важной особенностью получения обратной матрицы в данном случае является то, что ковариационная матрица Е является слабо обусловленной. Это приводит к тому, что при обращении таких матриц могут возникать достаточно серьезные ошибки. Все это требует обеспечения необходимой точности вычислительного процесса или использования специальных методов при вычислении таких матриц.
Пример. Написать выражение плотности вероятности для нормально распределенной двумерной случайной величины <Xv Х2)
при условии, что математические ожидания, дисперсии и ковариации этих величин имеют следующие значения:
Решение. Обратную ковариационную матрицу для матрицы (6.19) можно получить, используя следующее выражение обратной матрицы к матрице X:
где А — определитель матрицы X.
Аи, Л12, А21, А22 — алгебраические дополнения к соответствующим элементам матрицы X.
Тогда для матрицы ]г- ! получаем выражение
Так как а12 = 01О2Р и °2i =a 2 a iP> а a i2 a 2i = cyfст|р, то 

Функция плотности вероятности запишется в виде
Подставив исходные данные, получим следующее выражение для функции плотности вероятности
Видео:Корреляция и ковариация двумерной случайной величиныСкачать

Дана ковариационная матрица случайного вектора составить корреляционную матрицу
6.5.1 лПЧБТЙБГЙС. лПЬЖЖЙГЙЕОФ ЛПТТЕМСГЙЙ
рХУФШ ЪБДБОП ЧЕТПСФОПУФОПЕ РТПУФТБОУФЧП ( W , F, P) Й ДЧЕ УМХЮБКОЩЕ ЧЕМЙЮЙОЩ ξ Й η ОБ ОЕН.
пртедемеойе 6.5.1.1
лпчбтйбгйек ДЧХИ УМХЮБКОЩИ ЧЕМЙЮЙО ξ Й η ОБЪЩЧБЕФУС ЮЙУМП, ПРТЕДЕМСЕНПЕ РП ЖПТНХМЕ: M((ξ — Mξ)(η — Mη)).
| пвпъобюеойе: cov(ξ, η) = M((ξ — Mξ)(η — Mη)) | (6.5.1.1) |
пЮЕЧЙДОП, ЮФП cov(ξ, η) НПЦОП ОБКФЙ ФПМШЛП Ч ФПН УМХЮБЕ, ЛПЗДБ УХЭЕУФЧХАФ УППФЧЕФУФЧХАЭЙЕ НБФЕНБФЙЮЕУЛЙЕ ПЦЙДБОЙС.
ъбнеюбойе. жПТНХМБ (6.5.1.1) Ч ТБУЮЕФБИ ЙУРПМШЪХЕФУС ТЕДЛП. пРЙТБСУШ ОБ УЧПКУФЧБ НБФЕНБФЙЮЕУЛПЗП ПЦЙДБОЙС Й ДЙУРЕТУЙЙ, НПЦОП РПМХЮЙФШ ВПМЕЕ ХДПВОЩЕ ДМС ТБУЮЕФПЧ ЖПТНХМЩ.
M((ξ — Mξ)(η — Mη)) = M(ξη — ηMξ — ξMη + MξMη) =
= M(ξη) — MξMη — MξMη + MξMη = M(ξη) — MξMη. уМЕДПЧБФЕМШОП,
D(ξ + η) = Dξ + Dη + 2M(ξη) — 2MξMη = Dξ + Dη + 2cov(ξ, η) (уНПФТЙ 6.2.2).
D(ξ — η) = D(ξ + (-η)) = Dξ + D(-η) — 2M(ξ(-η)) — MξM(-η) =
= Dξ + D(-η) — 2(M(ξη) — MξMη) = Dξ + Dη — 2cov(ξ, η).
фептенб 6.5.1.1 (уЧПКУФЧБ ЛПЧБТЙБГЙЙ ДЧХИ УМХЮБКОЩИ ЧЕМЙЮЙО)
1. еУМЙ ξ Й η — ОЕЪБЧЙУЙНЩЕ УМХЮБКОЩЕ ЧЕМЙЮЙОЩ, ФП cov(ξ, η) = 0.
2. cov(ξ, η) = cov(η, ξ).
3. cov(ξ, ξ) = Dξ.
4. cov(ξ, Cη) = Ccov(ξ, η),
cov(Cξ, η) = Ccov(ξ, η), » C п R.
5. cov(ξ1 + ξ2, η) = cov(ξ1, η) + cov(ξ2, η);
cov(ξ, η1 + η2) = cov(ξ, η1) + cov(ξ, η2).
уРТБЧЕДМЙЧПУФШ ХФЧЕТЦДЕОЙК 2-3 УМЕДХЕФ ЙЪ ЖПТНХМЩ (6.5.1.2). дМС ДПЛБЪБФЕМШУФЧБ ПУФБМШОЩИ ЧПУРПМШЪХЕНУС УППФЧЕФУФЧХАЭЙНЙ УЧПКУФЧБНЙ НБФЕНБФЙЮЕУЛПЗП ПЦЙДБОЙС.
1) cov(ξ, η) = M(ξη) — MξMη = MξMη — MξMη = 0, ФБЛ ЛБЛ ДМС ОЕЪБЧЙУЙНЩИ η, ξ M(ξη) = MξMη.
4) cov(ξ, Cη) = M(ξCη) — MξM(Cη) = CM(ξη) — CMξMη = Ccov(ξ, η).
уРТБЧЕДМЙЧПУФШ ЧФПТПК ЖПТНХМЩ НПЦОП ДПЛБЪБФШ МЙВП БОБМПЗЙЮОП, МЙВП, ЙУРПМШЪХС УЧПКУФЧП 2.
уРТБЧЕДМЙЧПУФШ ЧФПТПК ЖПТНХМЩ НПЦОП ДПЛБЪБФШ МЙВП БОБМПЗЙЮОП, МЙВП ЙУРПМШЪХС УЧПКУФЧП 2.
умедуфчйе 6.5.1.1
1. cov(ξ, C) = cov(C, ξ) = 0, » C п R.
2. cov(ξ, Aξ + B) = cov(Aξ+B, ξ) = ADξ, » A, B п R.
1) рПУФПСООХА у НПЦОП ТБУУНБФТЙЧБФШ ЛБЛ УМХЮБКОХА ЧЕМЙЮЙОХ η, РТЙОЙНБАЭХА ПДОП ЪОБЮЕОЙЕ у У ЧЕТПСФОПУФША 1. пЮЕЧЙДОП, ЮФП Ч ЬФПН УМХЮБЕ УМХЮБКОЩЕ ЧЕМЙЮЙОЩ ξ Й η — ОЕЪБЧЙУЙНЩЕ УМХЮБКОЩЕ ЧЕМЙЮЙОЩ Й, УМЕДПЧБФЕМШОП, cov(ξ, η) = 0.
2) cov(ξ, Aξ + B) = cov(ξ, Aξ) + cov(ξ, B) = Acov(ξ, ξ) + 0 = ADξ.
ъбнеюбойе. уМЕДХЕФ РПНОЙФШ, ЮФП ЙЪ cov(ξ, η) = 0 ОЕ УМЕДХЕФ ОЕЪБЧЙУЙНПУФЙ УМХЮБКОЩИ ЧЕМЙЮЙО ξ, η.
оБРТЙНЕТ, РХУФШ ξ — УМХЮБКОБС ЧЕМЙЮЙОБ ДЙУЛТЕФОПЗП ФЙРБ, ЙНЕАЭБС УМЕДХАЭЙК ЪБЛПО ТБУРТЕДЕМЕОЙС:
| xk | -2 | -1 | 1 | 2 |
| pk | 1/4 | 1/4 | 1/4 | 1/4 |
Mξ = (1/4)ћ(-2) + (1/4)ћ(-1) + (1/4)ћ2 + (1/4)ћ1 = 0.
тБУУНПФТЙН η = ξ 2 (η Й ξ Ч ФБЛПН УМХЮБЕ ЪБЧЙУЙНЩЕ УМХЮБКОЩЕ ЧЕМЙЮЙОЩ!) ъБЛПО ТБУРТЕДЕМЕОЙС УМХЮБКОПК ЧЕМЙЮЙОЩ η ЙНЕЕФ ЧЙД:
| xk | 1 | 4 |
| pk | 1/2 | 1/2 |
Mη = (1/2)ћ1 + (1/2)ћ4 = 5/2.
cov(ξ, η) = M(ξη) — MξMη = M(ξћξ 2 ) — 0ћ(5/2) = M(ξ 3 ).
уМХЮБКОБС ЧЕМЙЮЙОБ ξ 3 ЙНЕЕФ ЪБЛПО ТБУРТЕДЕМЕОЙС:
| xk | -8 | -1 | 1 | 8 |
| pk | 1/4 | 1/4 | 1/4 | 1/4 |
Mξ 3 = (1/4)ћ(-8) + (1/4)ћ(-1) + (1/4)ћ1 + (1/4)ћ8 = 0. уМЕДПЧБФЕМШОП, cov (ξ, η) = 0, Б УМХЮБКОЩЕ ЧЕМЙЮЙОЩ СЧМСАФУС ЪБЧЙУЙНЩНЙ.
пртедемеойе 6.5.1.2
лПЬЖЖЙГЙЕОФПН лпттемсгйй ДЧХИ УМХЮБКОЩИ ЧЕМЙЮЙО ξ Й η ОБЪЩЧБЕФУС ЮЙУМП, ПРТЕДЕМСЕНПЕ РП ЖПТНХМЕ:
| пвпъобюеойе: |  | (6.5.1.5) |
ъбнеюбойе. пЮЕЧЙДОП, ЮФП ЛПЬЖЖЙГЙЕОФ ЛПТТЕМСГЙЙ ДЧХИ УМХЮБКОЩИ ЧЕМЙЮЙО НПЦОП ПРТЕДЕМЙФШ МЙЫШ Ч ФПН УМХЮБЕ, ЛПЗДБ УХЭЕУФЧХАФ УППФЧЕФУФЧХАЭЙЕ НБФЕНБФЙЮЕУЛЙЕ ПЦЙДБОЙС Й Dξ 

пРЙТБСУШ ОБ УЧПКУФЧБ ЛПЧБТЙБГЙЙ Й ДЙУРЕТУЙЙ (6.2.2), НПЦОП РПМХЮЙФШ ЕЭЕ ФТЙ ДПРПМОЙФЕМШОЩЕ ЖПТНХМЩ ДМС ЧЩЮЙУМЕОЙС ЛПЬЖЖЙГЙЕОФБ ЛПТТЕМСГЙЙ.
(уНПФТЙ ЖПТНХМХ 6.5.1.3). уМЕДПЧБФЕМШОП,
уПЧЕТЫЕООП БОБМПЗЙЮОП, ПРЙТБСУШ ОБ ЖПТНХМХ 6.5.1.4, НПЦОП ДПЛБЪБФШ, ЮФП:
фептенб 6.5.1.2 (уЧПКУФЧБ ЛПЬЖЖЙГЙЕОФБ ЛПТТЕМСГЙЙ)
1. еУМЙ ξ Й η — ОЕЪБЧЙУЙНЩЕ УМХЮБКОЩЕ ЧЕМЙЮЙОЩ, ФП ρ(ξ, η) = 0.
2. ρ(ξ, η) = ρ(η, ξ).
3. ρ(Cξ, η) = ρ(ξ, Cη) = signC ρ(Cξ, η), » C п R (C 
4. |ρ(ξ, η)| ≤ 1.
5. |ρ(ξ, η)| = 1 щ $ A, B п R (A 
уЧПКУФЧБ 1-2 УМЕДХАФ ЙЪ УЧПКУФЧ ЛПЧБТЙБГЙЙ.
4) фБЛ ЛБЛ ДЙУРЕТУЙС МАВПК УМХЮБКОПК ЧЕМЙЮЙОЩ (ЕУМЙ ПОБ УХЭЕУФЧЕФ) — ЧЕМЙЮЙОБ ОЕПФТЙГБФЕМШОБС, ФП ЙЪ ЖПТНХМ (6.5.1.7 Й 6.5.1.8) УМЕДХЕФ:
5) ( а ) (ОЕПВИПДЙНПУФШ)
Б) ρ(ξ, η) = 1 а ЙЪ ЖПТНХМЩ 6.5.1.8 УМЕДХЕФ, ЮФП 
ч ФБЛПН УМХЮБЕ, $ C п R:
фБЛЙН ПВТБЪПН, η = Aξ + B, ЗДЕ
ъБНЕФЙН, ЮФП 
В) ρ(ξ, η) = -1. тБУУХЦДБС БОБМПЗЙЮОП Й ЙУРПМШЪХС ЖПТНХМХ 6.5.1.7, НПЦОП ДПЛБЪБФШ, ЮФП
( ш ) η = Aξ + B; A, B п R Й A 
умедуфчйе 6.5.1.2
ρ(ξ, ξ) = 1.
ъбнеюбойе. уМЕДХЕФ РПНОЙФШ, ЮФП ЙЪ ρ(ξ, η) = 0 ОЕ УМЕДХЕФ ОЕЪБЧЙУЙНПУФШ УМХЮБКОЩИ ЧЕМЙЮЙО ξ Й η. (фБЛ ЛБЛ ρ(ξ, η) = 0 щ cov(ξ,η)=0; Б ЙЪ cov(ξ,η)=0 ОЕ УМЕДХЕФ, ЮФП ξ Й η ОЕЪБЧЙУЙНЩЕ УМХЮБКОЩЕ ЧЕМЙЮЙОЩ).
пртедемеойе 6.5.1.3
еУМЙ ρ(ξ, η) = 0, ФП УМХЮБКОЩЕ ЧЕМЙЮЙОЩ ξ Й η ОБЪЩЧБАФУС оелпттемйтхенщнй.
ъбнеюбойе. еУМЙ ρ(ξ, η) 
еУМЙ ρ(ξ, η) 


ьФП РТЙВМЙЦЕОЙЕ СЧМСЕФУС ОБЙМХЮЫЕН Ч УНЩУМЕ:
рХУФШ ОБ ЧЕТПСФОПУФОПН РТПУФТБОУФЧЕ ( W , F, P) ЪБДБО УМХЮБКОЩК ЧЕЛФПТ (ξ1, ξ2, . , ξn).
фБЛ ЛБЛ kij = cov(ξi, ξj) = cov(ξj, ξi) = kji, » i, j, ФП НБФТЙГБ K — УЙННЕФТЙЮОБС НБФТЙГБ (ПФОПУЙФЕМШОП ЗМБЧОПК ДЙБЗПОБМЙ); kii = Dξi, i= 1, . , n.
пртедемеойе 6.5.1.5
пРТЕДЕМЙФЕМШ ЛПЧБТЙБГЙПООПК НБФТЙГЩ ОБЪЩЧБЕФУС пвпвэеоопк дйуретуйек УМХЮБКОПЗП ЧЕЛФПТБ.
еУМЙ ξ1, ξ2, . , ξn РПРБТОП ОЕЪБЧЙУЙНЩ ЙМЙ cov(ξi, ξj) = 0, i 
фептенб 6.5.1.3
еУМЙ ЙЪЧЕУФОБ ЛПЧБТЙБГЙПООБС НБФТЙГБ л = (kij)n УМХЮБКОПЗП ЧЕЛФПТБ (ξ1, ξ2, . , ξn) Й ηi = ci1ξ1 + ci2ξ2 + . + cinξn, i = 1, . , n; ФП ЕУФШ
ФП ЛПЧБТЙБГЙПООБС НБФТЙГБ H = (hij), hij = cov(ηi, ηj) УМХЮБКОПЗП ЧЕЛФПТБ (η1, η2, . , ηn) НПЦЕФ ВЩФШ ОБКДЕОБ РП ЖПТНХМЕ:
H = CћKћC T .
уМЕДПЧБФЕМШОП, ЛПТТТЕМСГЙПООБС НБФТЙГБ R СЧМСЕФУС УЙННЕФТЙЮОПК.
еУМЙ УМХЮБКОЩЕ ЧЕМЙЮЙОЩ ξ1, ξ2, . , ξn РПРБТОП ОЕЪБЧЙУЙНЩ ЙМЙ ОЕЛПТТЕМЙТХЕНЩ, ФП ЛПТТЕМСГЙПООБС НБФТЙГБ R СЧМСЕФУС ЕДЙОЙЮОПК:
ъбнеюбойе. уМЕДХЕФ РПНОЙФШ, ЮФП ЮФП ЪОБС ЪБЛПО ТБУРТЕДЕМЕОЙС УМХЮБКОПЗП ЧЕЛФПТБ (ξ1, ξ2, . , ξn), НПЦОП ОБКФЙ ЮЙУМПЧЩЕ ИБТБЛФЕТЙУФЙЛЙ ЛПНРБОЕФ (ЕУМЙ ПОЙ УХЭЕУФЧХАФ).
оБРТЙНЕТ, ЕУМЙ ЧЕЛФПТ — УМХЮБКОБС ЧЕМЙЮЙОБ БВУПМАФОП ОЕРТЕТЧЩОПЗП ФЙРБ У РМПФОПУФША ТБУРТЕДЕМЕОЙС 
ъБРЙЫЙФЕ УБНПУФПСФЕМШОП УППФЧЕФУФЧХАЭЙЕ ЖПТНХМЩ ДМС УМХЮБКОПЗП ЧЕЛФПТБ ДЙУЛТЕФОПЗП ФЙРБ.
ъбдбюб 6.5.1.1 йЪЧЕУФОП, ЮФП Mξ = 1, Dξ = 2; η = 5ξ + 7. оБКФЙ cov(ξ, η).
cov(ξ, η) = cov(ξ, 5ξ + 7) = 5Dξ = 10.
ъбдбюб 6.5.1.2 йЪЧЕУФОП, ЮФП Mξ = 3, Dξ = 8. оБКФЙ ρ(ξ, η), ЕУМЙ η = — 15ξ + 2.
ъбдбюб 6.5.1.3 дБО ЪБЛПО ТБУРТЕДЕМЕОЙС УМХЮБКОПЗП ЧЕЛФПТБ (ξ1, ξ2) ДЙУЛТЕФОПЗП ФЙРБ:
 | 5 | 6 | 7 |
|---|---|---|---|
| 0 | 0,2 | 0 | 0 |
| 0,1 | 0,1 | 0,15 | 0 |
| 0,2 | 0,05 | 0,15 | 0,1 |
| 0,3 | 0,05 | 0,1 | 0,1 |
оБКФЙ: ЛПЧБТЙБГЙПООХА Й ЛПТТЕМСГЙПООХА НБФТЙГЩ УМХЮБКОПЗП ЧЕЛФПТБ (ξ1, ξ2).
1) рТЕЦДЕ ЧУЕЗП ОБКДЕН ЪБЛПО ТБУРТЕДЕМЕОЙС ЛБЦДПК ЛПНРПОЕОФЩ (БМЗПТЙФН УНПФТЙ 4.4.2)
| ξ1 | 5 | 6 | 7 |
|---|---|---|---|
| 0,4 | 0,4 | 0,2 |
Mξ1 2 = 25ћ0,4 + 36ћ0,4 + 49ћ0,2 = 34,2;
| ξ2 | 0 | 0,1 | 0,2 | 0,3 |
|---|---|---|---|---|
| 0,2 | 0,25 | 0,3 | 0,25 |
Mξ2 = 0ћ0,2 + 0,1ћ0,25 + 0,2ћ0,3 + 0,3ћ0,25 = 0,16;
Mξ2 2 = 0ћ0,1 + 0,01ћ0,25 + 0,04ћ0,3 + 0,09ћ0,25 = 0,037;
ъБНЕФЙН, ЮФП УМХЮБКОБС ЧЕМЙЮЙОБ ξ1ћξ2 РТЙОЙНБЕФ УМЕДХАЭЙЕ ЪОБЮЕОЙС Ч ЪБЧЙУЙНПУФЙ ПФ ЪОБЮЕОЙК ЛПНРПОЕОФ:
 | 5 | 6 | 7 |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0,1 | 0,5 | 0,6 | 0,7 |
| 0,2 | 1 | 1,2 | 1,4 |
| 0,3 | 1,5 | 1,8 | 2,1 |
уМЕДПЧБФЕМШОП, ЪБЛПО ТБУРТЕДЕМЕОЙС УМХЮБКОПК ЧЕМЙЮЙОЩ ξ1ћξ2 ЙНЕЕФ УМЕДХАЭЙК ЧЙД:
| xk | 0 | 0,5 | 0,6 | 0,7 | 1 | 1,2 | 1,4 | 1,5 | 1,8 | 2,1 |
| pk | 0,2 | 0,1 | 0,15 | 0 | 0,05 | 0,15 | 0,1 | 0,05 | 0,1 | 0,1 |
M(ξ1ξ2) = 0ћ0,2 + 0,1ћ0,5 + 0,6ћ0,15 + 0,7ћ0 + 0,05ћ1 + 0,15ћ1,2 +
+ 1,4ћ0,1 + 1,5ћ0,05 + 0,1ћ1,8 + 0,1ћ2,1 = 0,975.
Dξ1Dξ2 = 0,56ћ0,0114 = 0,006384 а ρ12 = ρ21 = 
ъбдбюб 6.5.1.4 йЪЧЕУФЕО ЪБЛПО ТБУРТЕДЕМЕОЙС УМХЮБКОПЗП ЧЕЛФПТБ:
 | 0 | 1 |
|---|---|---|
| -1 | 0,1 | 0,2 |
| 0 | 0,2 | 0,3 |
| 1 | 0 | 0,2 |
оБКФЙ НБФЕНБФЙЮЕУЛПЕ ПЦЙДБОЙЕ Й ДЙУРЕТУЙА УМХЮБКОПК ЧЕМЙЮЙОЩ q = 2ξ1 + ξ 2 2.
уМЕДПЧБФЕМШОП, РТЕЦДЕ ЧУЕЗП ПРТЕДЕМЙН ЪБЛПОЩ ТБУРТЕДЕМЕОЙС ξ1 Й ξ2.
| ξ1 | xk | 0 | 1 |
|---|---|---|---|
| pk | 0,3 | 0,7 |
| ξ2 | xk | -1 | 0 | 1 |
|---|---|---|---|---|
| pk | 0,3 | 0,5 | 0,2 |
| ξ2 2 | xk | 0 | 1 |
|---|---|---|---|
| pk | 0,5 | 0,5 |
| ξ1ξ2 2 | xk | 0 | 1 |
|---|---|---|---|
| pk | 0,6 | 0,4 |
cov(ξ1, ξ2 2 ) = 0,4 — 0,7 ћ 0,5 = 0,05. фБЛЙН ПВТБЪПН,
M q = 2ћ0,7 + 0,5 = 1,9;
D q = 4ћ0,21 + 0,25 + 2ћ0,05 = 0,84 + 0,25 + 0,1 = 1,29.
ъбдбюб 6.5.1.5 йЪЧЕУФОБ РМПФОПУФШ ТБУРТЕДЕМЕОЙС УМХЮБКОПЗП ЧЕЛФПТБ (ξ, η):
оБКФЙ ЛПЧБТЙБГЙА УМХЮБКОЩИ ЧЕМЙЮЙО ξ, η.
Cov(ξ, η) = π/2 — 1 — π 2 /16.
(чУЕ ЧЩЮЙУМЕОЙС РТПЧЕТШФЕ!)
ъБДБЮЙ ДМС УБНПУФПСФЕМШОПЗП ТЕЫЕОЙС.
ъбдбюб 6.5.1.1(у) дБО ЪБЛПО ТБУРТЕДЕМЕОЙС УМХЮБКОПЗП ЧЕЛФПТБ (ξ1, ξ2):
 | 0 | 2 | 5 |
|---|---|---|---|
| 1 | 0,1 | 0 | 0,2 |
| 2 | 0 | 0,3 | 0 |
| 4 | 0,1 | 0,3 | 0 |
уПУФБЧЙФШ ЛПЧБТЙБГЙПООХА Й ЛПТТЕМСГЙПООХА НБФТЙГЩ.
ъбдбюб 6.5.1.2(у) ъБДБО УМХЮБКОЩК ЧЕЛФПТ (ξ, η). йЪЧЕУФОП, ЮФП Mξ = 0, Mη = 2, Dξ = 2, Dη = 1, ρ(ξ, η) = — 
ъбдбюб 6.5.1.3(у) йЪЧЕУФОБ РМПФОПУФШ ТБУРТЕДЕМЕОЙС УМХЮБКОПЗП ЧЕЛФПТБ (ξ, η):
D — ФТЕХЗПМШОЙЛ, ПЗТБОЙЮЕООЩК РТСНЩНЙ x + y = 1, x = 0, y = 0. оБКФЙ ЛПЬЖЖЙГЙЕОФ ЛПТТЕМСГЙЙ.
© гЕОФТ ДЙУФБОГЙПООПЗП ПВТБЪПЧБОЙС пзх, 2000-2002
💥 Видео
Теория вероятностей #19: ковариация, корреляция, зависимость двух случайных величинСкачать

Случайный вектор двумерной случайной величиныСкачать

Математика #1 | Корреляция и регрессияСкачать

Теория вероятностей #25: Ковариация и корреляция / ковариационная матрицаСкачать

Оценка ковариационной матрицыСкачать

Математика без Ху!ни. Ряд распределения дискретной случайной величины. Мат ожидание и дисперсия.Скачать

Биноминальное распределениеСкачать

Теория вероятностей #12: случайная величина, плотность и функция распределенияСкачать

Ковариация. ТемаСкачать

Расчет корреляционных зависимостей в Microsoft ExcelСкачать

О корреляционной функции и её аналитическом вычисленииСкачать

8. Двумерные случайные векторы. КовариацияСкачать

Нахождение функции распределения для двумерного случайного вектора по плотностиСкачать

Коэффициент корреляции. Дискретное распределениеСкачать

Функция распределения и плотность распределенияСкачать

Теория вероятностей. Подготовка к контрольной. Ковариационные матрицыСкачать

Расчет коэффициента корреляции в ExcelСкачать

Собственные векторы и собственные значения матрицыСкачать