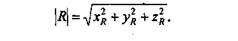Тема9. Построение реалистических изображений
В этом разделе мы рассмотрим методы, которые позволяют получить более-менее реалистичные изображения для объектов, моделируемых многогранниками и полигональными сетками.
Модели отражения света
Рассмотрим, как можно определить цвет пикселов изображения поверхности согласно интенсивности отраженного света при учете взаимного расположения поверхности, источника света и наблюдателя.
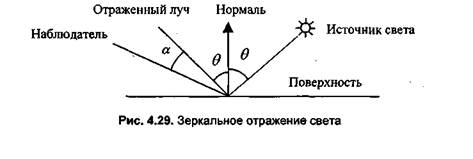
Зеркальное отражение света.Угол между нормалью и падающим лучом (Θ) равен углу между нормалью и отраженным лучом. Падающий луч, отраженный, и нормаль располагаются в одной плоскости (рис. 4.29).
Поверхность считается идеально зеркальной, если на ней отсутствуют какие либо неровности, шероховатости. Собственный цвет у такой поверхности не наблюдается. Световая энергия падающего луча отражается только по линии отраженного луча. Какое-либо рассеяние в стороны от этой линии отсутствует. В природе, вероятно, нет идеально гладких поверхностей, поэтому полагают, что если глубина шероховатостей существенно меньше длины волны излучения, то рассеивания не наблюдается. Для видимого спектра можно принять, что глубина шероховатостей поверхности зеркала должна быть существенно меньше 0.5 мкм
Если поверхность зеркала отполирована неидеально, то наблюдается зависимость интенсивности отраженного света от длины волны — чем больше длина волны, тем лучше отражение. Например, красные лучи отражаются сильнее, чем синие.
При наличии шероховатостей имеется зависимость интенсивности отраженного света от угла падения. Отражение света максимально для углов, близких к 90 градусам.
Падающий луч, попадая на слегка шероховатую поверхность реального зеркала, порождает не один отраженный луч, а несколько лучей, рассеиваемые по различным направлениям. Зона рассеивания зависит от качества полировки и может быть описана некоторым законом распределения. Как правило, форма зоны рассеивания симметрична относительно линии идеального зеркально отраженного луча. К числу простейших, но достаточно часто используемых, относится эмпирическая модель распределения Фонга, согласно которой интенсивность зеркально отраженного излучения пропорциональна (cosа) p , где а— угол отклонения от линии идеально отраженного луча. Показатель р находится в диапазоне от 1 до 200 и зависит от качества полировки. Запишем это таким образом:
где I— интенсивность излучения источника, Ks— коэффициент пропорциональности, который изменяется от 0 до 1.
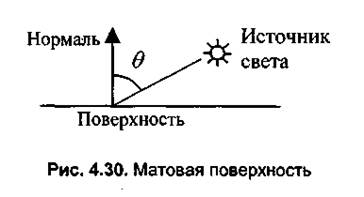
Диффузное отражение.Этот вид отражения присущ матовым поверхностям. Матовой можно считать такую поверхность, размер шероховатостей которой уже настолько велик, что падающий луч рассеивается равномерно во все стороны. Такой тип отражения характерен, например, для гипса, песка бумаги. Диффузное отражение описывается законом Ламберта, согласно которому интенсивность отраженного света пропорциональна косинусу угла между направлением на точечный источник света и нормалью к поверхности (рис. 4.30).
где I— интенсивность источника света, Kd— коэффициент, который учитывает свойства материала поверхности. Значение Kd находится в диапазоне от 0 до 1 . Интенсивность отраженного света не зависит от расположения наблюдателя.
Матовая поверхность имеет свой цвет. Наблюдаемый цвет матовой поверхности определяется комбинацией собственного цвета поверхности и цвета излучения источника света.
При создании реалистичных изображений следует учитывать то, что в природе, вероятно, не существует идеально зеркальных или полностью матовых поверхностей. При изображении объектов средствами компьютерной графики обычно моделируют сочетание зеркальности и диффузного рассеивания в пропорции, характерной для конкретного материала. В этом случае модель отражения записывают в виде суммы диффузной и зеркальной компонент:
где константы Kd, KS определяют отражательные свойства материала.
Согласно этой формуле интенсивность отраженного света равна нулю для некоторых углов Θ и а. Однако в реальных сценах обычно нет полностью затемненных объектов, следует учитывать фоновую подсветку, освещение рассеянным светом, отраженным от других объектов. В таком случае интенсивность может быть эмпирически выражена следующей формулой:
где Iа — интенсивность рассеянного света, Ка — константа, изменяется от 0 до 1.
Можно еще усовершенствовать модель отражения, если учесть то, что энергия от точечного источника света уменьшается пропорционально квадрату расстояния. Использование такого правила вызывает сложности, поэтому на практике часто реализуют модель, выражаемую эмпирической формулой:
где R — расстояние от центра проекции до поверхности, k — константа.
Как определить цвет закрашивания точек объектов в соответствии с данной моделью? Наиболее просто выполняется расчет в градациях серого цвет (например, для белого источника света и серых объектов). В данном случае интенсивность отраженного света соответствует яркости. Сложнее обстоит дело с цветными источниками света, освещающими цветные поверхности. Например, для модели RGB составляются три формулы расчета интенсивности отраженного света для различных цветовых компонент. Коэффициент! Ка и Kd различны для разных компонент — они выражают собственный цвет поверхности. Поскольку цвет отраженного зеркального луча равен цвету источника, то коэффициент Ks будет одинаковым для всех компонент цветовой модели. Цвет источника света выражается значениями интенсивности I для соответствующих цветовых компонент.
Алгебра векторов
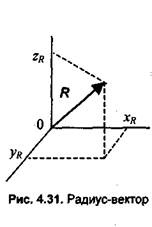
Здесь уместно сделать небольшое отступление от темы. Рассмотрим элементы алгебры векторов. Вектором называется отрезок прямой, соединяющий некоторые точки пространства А и В. Направление вектора — от начальной точки А к конечной точке В. Радиус-вектор R — это вектор, с начальной точкой в центре координат. Координатами радиус-вектора являются координаты конечной точки (рис. 4.31). Длина радиус-вектора часто называется модулем, обозначается как R|и вычисляется следующим образом:
Единичный вектор — это вектор, длина которого равна единице. Перечислим основные операции над векторами.
1. Умножение вектора на число X = Va. Результат — вектор X, длина которого в а раз больше вектора V. Если число а положительно, то направление вектора X совпадает с вектором V. При а
Видео:Раскрываю секрет магии с зеркалом #зеркало #секрет #физикаСкачать

Отражение в зеркале вектор
В. Г. Автор. Векторная и тензорная алгебра для будущих физиков и техников
.Геометрическое определение вектора
.Алгебраические операции над направленными отрезками
..Сложение направленных отрезков
..Умножение направленных отрезков на число
..Параллельное проектирование вектора в пространстве
. Проекция точки на плоскость
. Проекция вектора на плоскость
..Ортогональная проекция вектора в пространстве
. Ортогональная проекция вектора на плоскость
. Ортогональная проекция вектора на прямую и направленную ось
..Векторы в трехмерном геометрическом пространстве
..Линейная зависимость векторов и размерность пространства
..Различные формы записи векторов
..Линейные операции над векторами в координатной форме
. Свойства скалярного умножения
. Скалярное умножение в декартовых координатах
..Некоторые примеры использования скалярного умножения
..Площадь параллелограмма, построенного на векторах
..Задачи на применение определителей
..Определитель третьего порядка и его свойства
..Векторное умножение векторов базиса декартовой системы координат
.Ковариантные и контравариантные координаты вектора
..Индексная форма записи для выражений с определителями
..Свойства символов Веблена
..Операция векторного умножения в произвольных косоугольных координатах
.Линейные преобразования или операторы
.Линейный оператор и его матрица
.Доказательство теоремы об определителе
.Общие определения алгебраических операций с тензорами
.Примеры на применение тензоров в физике
..Задачи на тождественные преобразования
Векторы удобны для работы с теми или иными величинами, обладающими «векторными» свойствами. Векторы позволяют задать такие величины, т.е. дать им численную характеристику. Но на проблеме описания величин потребности науки и практики никогда не исчерпываются. Любая теория, прежде всего исследует связи или зависимости между изучаемыми величинами. Для отражения связей между различными величинами в математике вводится понятие функции. Наиболее простой, досконально проработанной и исследованной во всех деталях, является теория функций числового аргумента. То, что координатный метод позволяет использовать все достижения теории функций для описания функциональных зависимостей между векторными величинами можно считать одним из главных его достоинств. Для того чтобы задать функциональную зависимость между двумя векторными величинами 


Имеющийся набор хорошо исследованных элементарных, и не очень элементарных и совсем не элементарных функций позволяет задать практически любую мыслимую зависимость между векторными величинами. Наиболее простой вид зависимости между векторами определяют линейные функции:


При всей своей простоте линейная зависимость обладает широкими выразительными возможностями. К тому же, если ограничить область исследования достаточно малой областью изменения величин, зависимость между ними почти всегда можно считать приближенно линейной.
Линейной является зависимость между дифференциалами координат векторов 


Последнее обстоятельство особенно важно для математического анализа.
Особую роль линейные функции получили в последнее время благодаря широкой компьютеризации и порожденному ей стремительному развитию численных методов, которые, так или иначе, сводят любую задачу к решению больших систем линейных уравнений.
Подробно теория линейных функций или линейных преобразований, как ее часто называют, изучается в курсе линейной алгебры. Мы остановимся на этом предмете только для того, чтобы на отдельных примерах продемонстрировать те идеи, которые имеют отношение к нашему предмету.
Линейные функции часто записывают в виде операторов. Принципиальной разницы между понятием оператора и функции не существует. Разница в основном терминологическая. На языке функций мы можем сказать, что 





Каждый линейный оператор может быть задан в виде линейных уравнений либо в матричной форме:

Но кроме этих двух, линейный оператор может быть задан и многими другими способами, например, при помощи такой инструкции: повернуть вектор, стоящий на входе на угол φ относительно оси x в направлении от оси y к оси z . Для выполнения этой инструкции нет необходимости прибегать к матричной записи, хотя она и может быть сделана. Поэтому, принято различать сам оператор, который выполняет некоторые действия с векторами, и его матрицу, как некоторый, но не единственный способ выражения этих действий.
Пусть 










Так как 


Матрицу, выполняющую преобразование через ковариантные координаты будем обозначать 



Мы видим, что с индексами элементов матрицы линейного преобразования можно производить операции по изменению их типа точно так же, как с индексами координат векторов. При этом мы получим четыре различные матрицы, которые при их правильном использовании, т.е. с координатами векторов соответствующего типа, приводят к одинаковому геометрическому результату.
Векторы также могут быть заданы в различных координатных системах. Пусть выражение 

Умножим правую и левую части данного равенства на матрицу 


Отсюда мы получаем связь между матрицами одного и того же преобразования в различных координатных системах:

Также можно доказать, что 
Если подходить к этому закону как к формальному преобразованию индексов, то нетрудно заметить полную идентичность этого преобразования с правилом преобразования индексов ковариантных и контравариантных координат векторов. Поэтому, элементы матриц 







Прежде чем переходить к конкретным примерам линейных преобразований, получим простое правило, которое позволит нам в некоторых случаях легко вычислить их координаты.
Пусть 

Символом 





Теперь мы можем сформулировать следующее правило .
Для того, чтобы найти матрицу координат линейного преобразования 
1. «Подействовать» преобразованием на векторы базиса и найти результат этого действия.
2. Найти координаты преобразованных векторов базиса.
3. Составить матрицу из координат преобразованных векторов базиса как из столбцов.
Поставим задачу найти координаты линейного оператора 


В соответствии с полученным нами правилом, найдем векторы, которые получаются в результате действия преобразования на векторы базиса. Для этого разложим произвольный (для определенности возьмем вектор 







При отражении в зеркале вектор 


Для произвольного вектора:

Теперь мы можем записать преобразованные базисные векторы в координатной форме.



На последнем этапе мы строим матрицу преобразования из найденных столбцов.
Задача решена. Общий метод работает, но не всегда общий метод является самым простым и коротким. Попробуем решить задачу иначе. Пусть вектор 

Разложим вектор 











Таким образом: 
В данном случае мы воспользовались преобразованиями в индексной форме, но если перейти к матричной форме записи, то мы получим тот же самый результат:

Следует заметить, что на этот раз мы не делали никаких предположений о базисных векторах, следовательно, формулу можно считать действительной для самого общего случая.
В декартовой системе координат мы можем воспользоваться более привычными обозначениями для проекций вектора единичной нормали n :

Для того, чтобы лучше понять смысл полученного выражения конкретизируем условие. Пусть




Дадим графическую иллюстрацию полученному решению.

Серьезной проблемой при решении задач на стереометрию оказывается сложность в выполнении пространственных чертежей. Данная задача хороша тем, что вектор n лежит в плоскости xoy . При этом вертикальная составляющая вектора 

Видео:Дед не узнал своё отражение в зеркале и стал с ним разговаривать!Скачать

Отражение в зеркале вектор
Пойдем дальше. Вы видели, что в физике имеется масса примеров применимости правила правой и левой руки. В самом деле, когда мы изучали векторный анализ, то узнали о правиле правой руки, которым необходимо пользоваться, чтобы получить правильный момент количества движения и момент силы, магнитное поле и т. п. Например, сила, действующая на заряд в магнитном поле, равна 



Представьте себе, что какой-то озорной чертик, решив подшутить над физиками, пробрался во все лаборатории и всюду заменил слово «правое» на «левое». И в результате, где было написано правило правой руки, мы вынуждены были бы пользоваться правилом левой руки. Ну что ж, физики бы просто не заметили этого, ибо ни к какому изменению в физических законах это бы не привело, разумеется, если физические законы симметричны.
Покажем это на примере. Вы знаете, что существуют два сорта векторов. Имеются обыкновенные, «настоящие» векторы, подобные, например, отрезку расстояния 
Фиг. 52.2. Отрезок в пространстве и его зеркальное отражение.
Но второй сорт векторов, связанных с вращением, имеет совсем другую природу. Представьте себе нечто вращающееся в трехмерном пространстве (фиг. 52.3). Если посмотреть на это в зеркало, то вращение будет происходить так, как показано на рисунке, т. е. как зеркальное изображение первоначального вращения. Условимся теперь представлять зеркальное вращение с помощью того же самого правила. В результате мы получим «вектор», который в отличие от полярного вектора не изменяется при отражении и оказывается перевернутым по отношению к полярному вектору и геометрии всего пространства. Такой вектор мы называем аксиальным.
Фиг. 52.3. Вращающееся колесо и его зеркальное отражение.
Заметьте, что направление «вектора» угловой скорости не изменяется.
Если физический закон симметрии относительно отражения правилен, то уравнения должны быть устроены так, чтобы при изменении знака каждого аксиального вектора и каждого векторного произведения (что соответствует отражению) ничего не произошло. Например, когда мы пишем формулу для момента количества движения 










Давайте посмотрим на примере, как это все получается. Пусть у нас имеются два магнита, похожих на изображенные на фиг. 52.4. Один из магнитов выглядит в точности так, как зеркальное отражение другого, т. е. витки его накручены в другую сторону, и все, что происходит внутри катушки, должно быть в точности обращено в другую сторону; ток течет, как это показано на рисунке. Теперь из законов магнетизма (которые вы хотя еще и не знаете официально, но, по-видимому, помните из школьного курса) получается, что магнитное поле направлено так, как это показано на рисунке. Там, где у первого магнита южный полюс, у другого магнита будет северный, ибо у него ток течет в другую сторону, а магнитное поле перевернуто. Таким образом, выходит, что при переходе от правой системы к левой мы действительно должны заменить северный полюс на южный!
Фиг. 52.4. Электромагнит и его зеркальное отражение.
Но северный и южный полюсы — это просто договоренность, и замена их еще ничего не означает. Давайте посмотрим на само явление. Предположим, что электрон движется от нас через магнитное поле перпендикулярно к плоскости страницы. Тогда, если воспользоваться формулой для силы 
А теперь проделаем тот же опыт с зеркально отраженным магнитом: пошлем электрон в соответствующем направлении. Теперь на него будет действовать обратная сила. Вычислив ее по тем же правилам, мы получим правильный результат: соответствующее движение будет зеркальным отражением предыдущего!
🎬 Видео
Сферические зеркала, построение изображения в сферическом зеркале. 8 класс.Скачать

Физика 9 класс (Урок№28 - Отражение света. Плоское зеркало.)Скачать

Отражение света от плоского зеркалаСкачать

Урок 200 (осн). Построение изображения в плоском зеркалеСкачать

ОТРАЖЕНИЕ В ЗЕРКАЛЕ 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать

Отражение света от выпуклого зеркалаСкачать

Проверил лайфхак отражение видно в зеркалеСкачать

Жуткое отражение в зеркале (до конца).Скачать

Отражение в зеркале изменило девушку #shortsСкачать

Изображение в вогнутом зеркалеСкачать

Сферические зеркала, построение изображения в сферическом зеркале. Практическая часть. 8 класс.Скачать

Отражение света от зеркалаСкачать

Отражение света, законы отражения, плоские зеркала. 8 класс.Скачать

Отражение в зеркалеСкачать

Таинственный момент: отражение в зеркале опережает движения смотрящегося в негоСкачать

Многократное отражение светаСкачать

Изображение предмета в плоском зеркалеСкачать

отражение в зеркалеСкачать