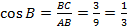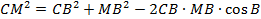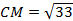Неравенство треугольников теорема косинусов

Теорема косинусов — теорема евклидовой геометрии, которая обобщающает теорему Пифагора.

Теорема косинусов:

Для плоского треугольника, у которого стороны a, b, c и угол α, который противолежит стороне a, справедливо соотношение:

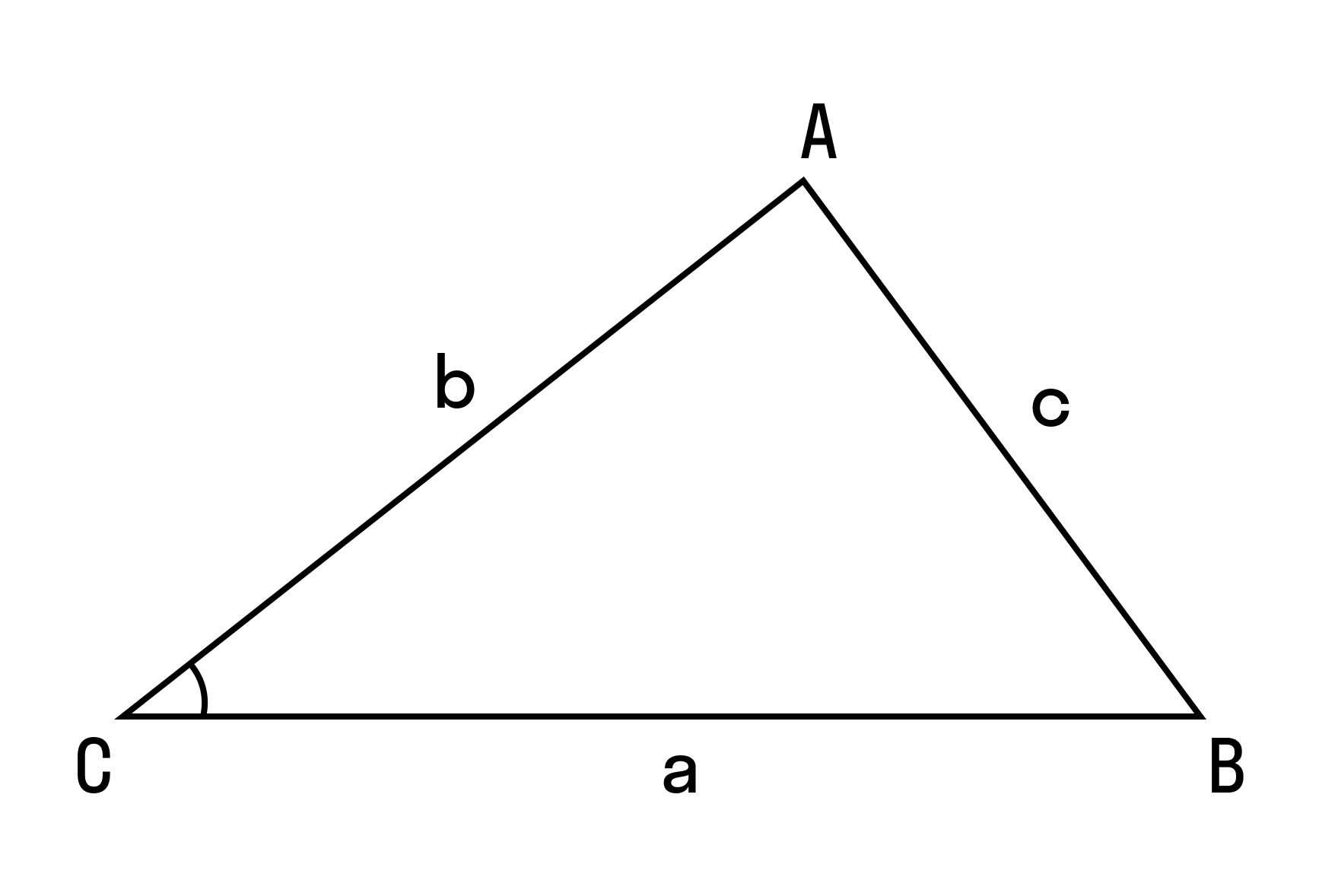
Квадрат стороны треугольника равняется сумме квадратов 2-х других сторон минус удвоенное произведение этих сторон на косинус угла между ними.

Видео:ТЕОРЕМА СИНУСОВ И ТЕОРЕМА КОСИНУСОВ. Тригонометрия | МатематикаСкачать

Следствие из теоремы косинусов.

• Теорема косинусов используется для определения cos угла треугольника:

h 2 = a 2 — (c – b cos α) 2 (2)

Приравниваем правые части уравнений (1) и (2):

b 2 — (b cos α) 2 = a 2 — (c — b cos α) 2

a 2 = b 2 + c 2 — 2bc cos α.

Если 1-н из углов при основании тупой (высота упирается в продолжение основания), полностью аналогичен рассмотренному выше.

Определить стороны b и c:

Видео:Неравенства треугольника. 7 класс.Скачать

Теорема косинусов и синусов

О чем эта статья:

Видео:9 класс, 14 урок, Теорема косинусовСкачать

Формулировка и доказательство теоремы косинусов

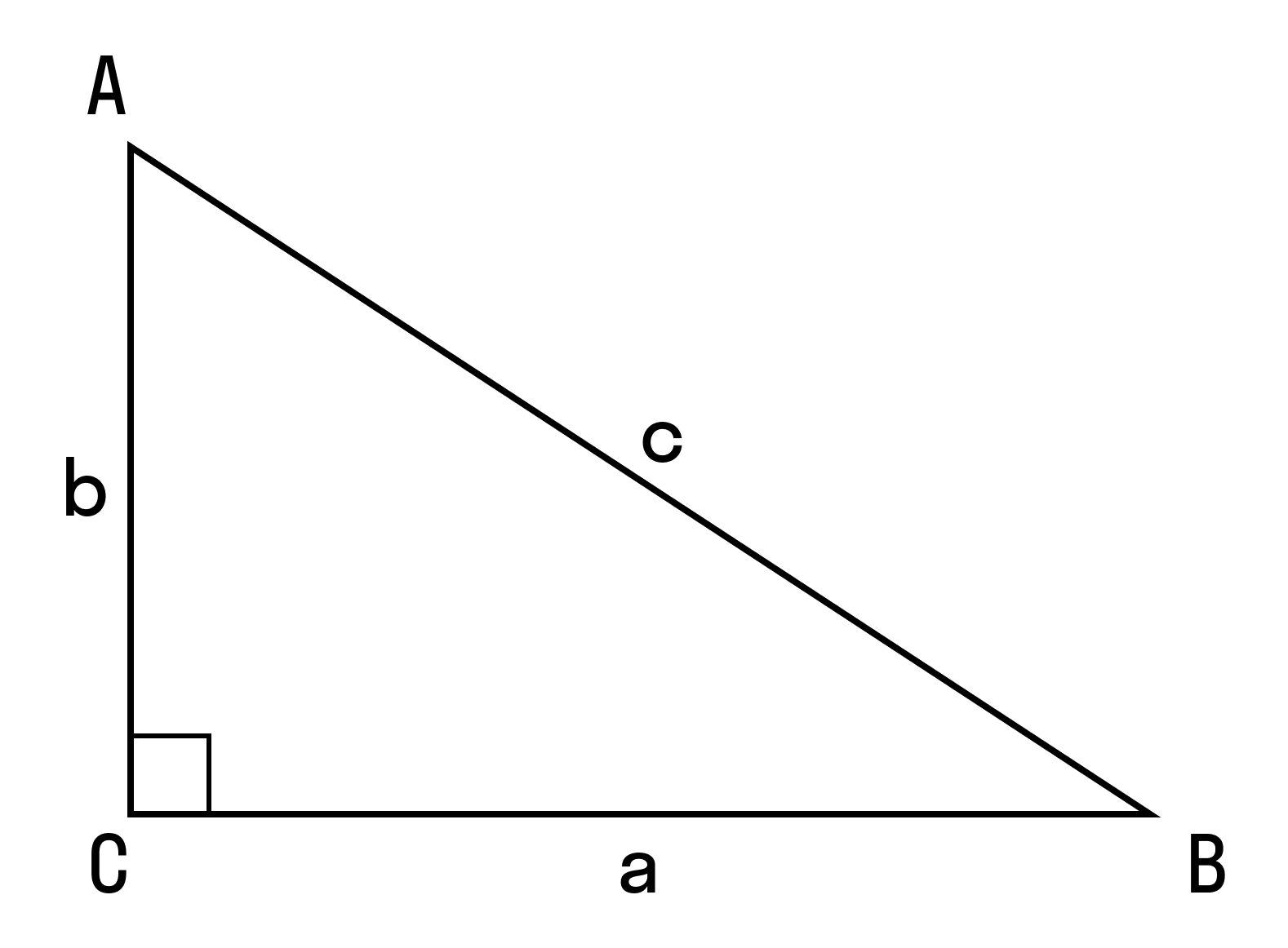
Для начала вспомним теорему Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Формула Теоремы Пифагора:

a 2 > + b 2 > = c 2 >, где a, b — катеты, с — гипотенуза.

Теорема косинусов звучит так: квадрат стороны треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон на косинус угла между ними.

Формула теоремы косинусов:

a 2 = b 2 + c 2 — 2bc cos α

В доказательстве теоремы косинусов используем формулу длины отрезка в координатах. Рассмотрим данную формулу:

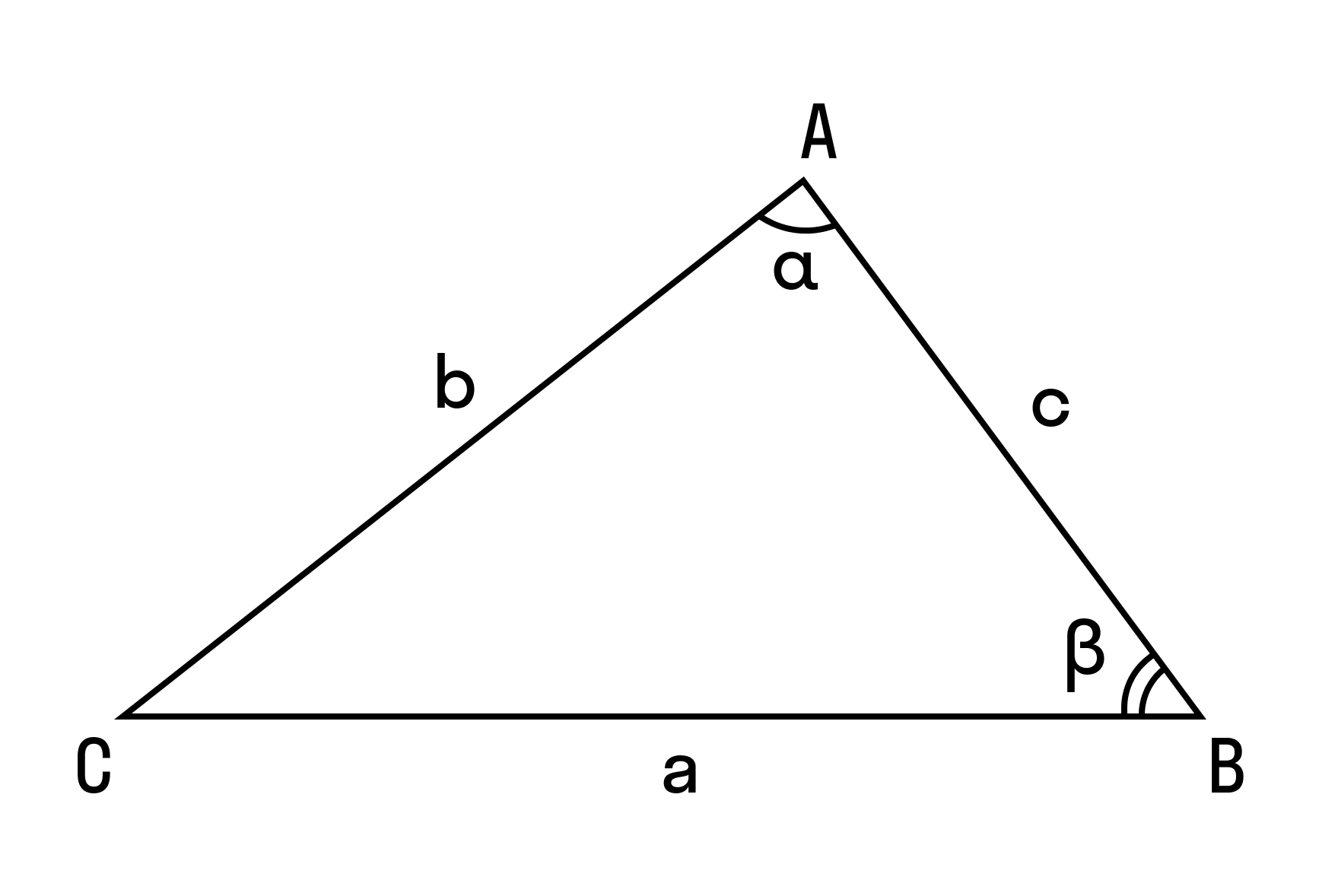
В доказательстве теоремы косинусов BC — это сторона треугольника АВС, которая обозначена буквой а. Введем удобную систему координат и найдем координаты нужных нам точек. У точки В координаты (с; 0).
Координаты точки С — (b cos α; b sin α) при α ∈ (0° ; 180°).

cos 2 α + sin 2 α = 1 — основное тригонометрическое тождество.

BC 2 = a 2 = (b cos α — c) 2 + b 2 sin 2 α = b 2 cos 2 α + b 2 sin 2 α — 2bc cos α + c 2 = b 2 (cos 2 α + sin 2 α) — 2bc cos α + c 2

Что и требовалось доказать.

Совет: чтобы быстрее разобраться в сложной теме, запишитесь на онлайн-курсы по математике для детей и подростков.

С помощью теоремы косинусов можно найти косинус угла треугольника:

• Когда b 2 + c 2 — a 2 > 0, угол α будет острым.
• Когда b 2 + c 2 — a 2 = 0, угол α будет прямым.
• Когда b 2 + c 2 — a 2

Сформулируем еще одно доказательство теоремы косинусов.

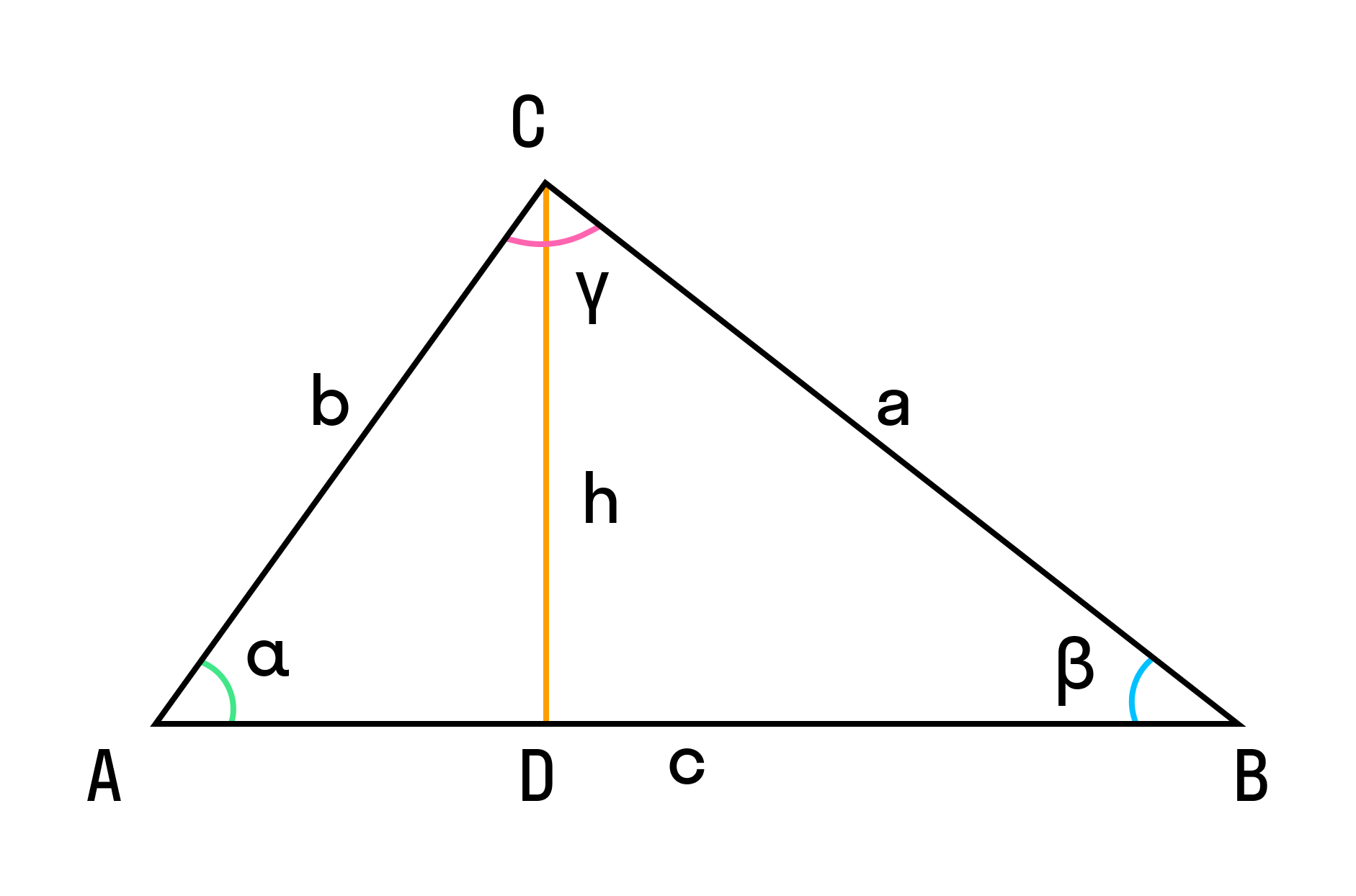
Пусть нам дан треугольник ABC, в котором из вершины C на сторону AB опустили высоту CD. Это значит:

• AD = b × cos α,
• DB = c – b × cos α.

Запишем теорему Пифагора для двух прямоугольных треугольников ADC и BDC:

• h 2 = b 2 — (b × cos α) 2
• h 2 = a 2 — (c – b × cos α) 2

Приравниваем правые части уравнений:

• b 2 — (b × cos α) 2 = a 2 — (c — b × cos α) 2

• a 2 = b 2 + c 2 — 2bc × cos α

Если один из углов при основании тупой (высота упирается в продолжение основания), полностью аналогичен рассмотренному выше.

Определим стороны b и c:

• b 2 = a 2 + c 2 — 2ac × cos β;
• c 2 = a 2 + b 2 — 2ab × cos γ.

Видео:Теоремы синусов и косинусов | Ботай со мной #029 | Борис ТрушинСкачать

Формулировка теоремы для каждой из сторон треугольника

Теорема косинусов справедлива для всех сторон треугольника, то есть:

a 2 = b 2 + c 2 — 2bc cos α

b 2 = c 2 + a 2 — 2ca cos β

c 2 = a 2 + b 2 — 2ab cos γ

Теорема косинусов может быть использована для любого вида треугольника.

Видео:✓ Тригонометрические формулы | Борис ТрушинСкачать

Косинусы углов треугольника

Теорема косинусов позволяет найти как косинус, так и угол треугольника. Найдём косинусы углов:

Видео:ТЕОРЕМА КОСИНУСОВ. Задачи на произвольные треугольникиСкачать

Определение угла с помощью косинуса

А теперь обратим внимание на углы.

Как мы уже знаем, косинус угла из промежутка (0°; 180°) определяет угол (в отличие от его синуса).

Пусть нам дана единичная полуокружность. Если нам задан cos α, то нам задана точка на верхней полуокружности и задан угол α. Следовательно, cos α однозначно определяет точку М(cos α; sin α), и однозначно определяется угол ∠AOM.

Видео:Геометрия 9 класс (Урок№16 - Теорема косинусов.)Скачать

Рассмотрение пределов изменения cos α и sin α

Рассмотрим пределы изменения синуса и косинуса α. Вспомним, что если α — угол треугольника, то он лежит в пределах от 0° до 180°.

Предел изменения косинуса: -1 0, то α ∈ (0°;90°)
Если cos α

Видео:Теорема косинусов | ДоказательствоСкачать

Примеры решения задач

При помощи теоремы косинусов можно решать задачки по геометрии. Рассмотрим интересные случаи.

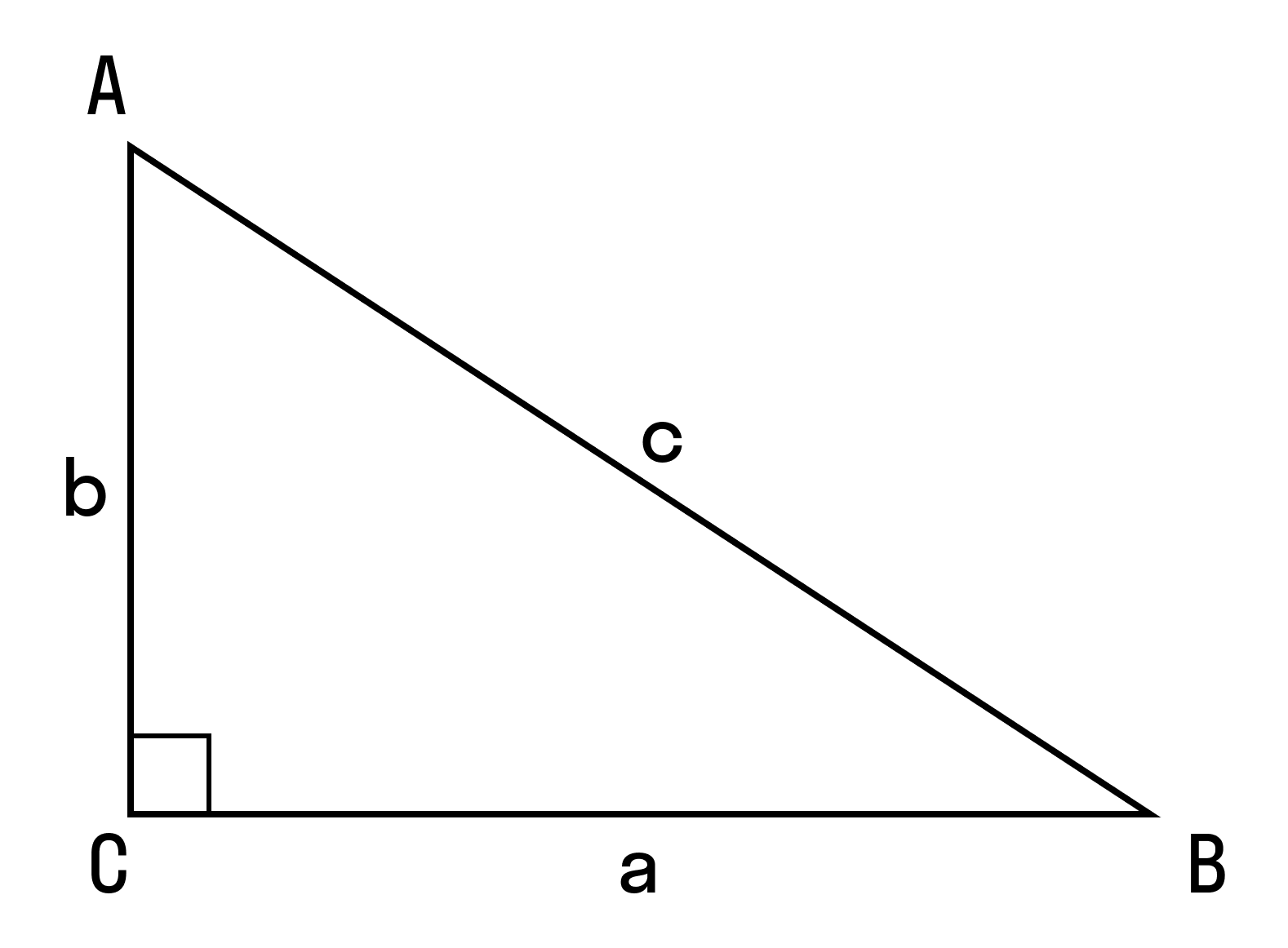
Пример 1. Дан треугольник АВС. Найти длину СМ.

∠C = 90°, АВ = 9, ВС = 3, AM/MB = 1/2, где М — точка на гипотенузе АВ.

Так как АМ + МВ = 9, а AM/MB = 1/2, то АМ = 3, МВ = 6.
Из треугольника АВС найдем cos B:

Из треугольника СМВ по теореме косинусов найдём СМ:

Пример 2. Дан треугольник АВС, в котором a2+ b22 + b 2 2 , то cos C 2 = a 2 + b 2 , то ∠C = 90°.

• Если c 2 2 + b 2 , то ∠C — острый.

Видео:7 класс, 34 урок, Неравенство треугольникаСкачать

Теорема косинусов. Следствия из теоремы косинусов

Разделы: Математика

Цель урока:

• Повторить ранее изученный теоретический материал, изучить теорему косинусов и её следствия, учить делать теоретические обобщения.
• Развивать логику мышления при решении специально подобранных задач.
• Воспитывать потребность в доказательстве высказанной гипотезы.

Тип урока: урок ознакомления с новым материалом.

Оборудование урока: ноутбук, мультимедийный проектор, интерактивная доска.

Видео:Самый короткий тест на интеллект Задача Массачусетского профессораСкачать

Ход урока

I. Сообщение темы, цели и задач урока. Мотивация учебной деятельности.

II. Подготовка к изучению нового материала через повторение и актуализацию опорных знаний

(Фронтальная работа с классом)

Рис. 1

Рис. 2

Рис. 3

1. Рис.1. Как найти гипотенузу прямоугольного треугольника, если известны длины катетов a и b.
2. Рис.1. Как найти катет a, если известны длина гипотенузы c и В.
3. Рис.1. Как найти катет b, если известны длина гипотенузы с и А.
4. Чему равен квадрат расстояния между точками А (х₁; у₁) и В (х₂; у₂).
5. Рис. 2. Найти координаты точки A, если OA = a и угол между положительной полуосью OX и лучом OA равен .
6. Рис. 3. a | | b. Что вы можете сказать об углах 1 и 2. Односторонние, 1 +2 = 180° . Если 2 = , тогда 1 = 180° —
7. Чему равны: sin(180° — ) = ? cos(180° — ) = ?

III. Изучение нового материала.

Учащимся предлагается задача на готовом чертеже. Теорема синусов для решения этой задачи не подходит, поскольку из трех известных элементов треугольника не известны сторона и противолежащий угол.

Первый способ решения задачи. (Устно)

ABC,

A

Проведём CH – высоту.

1) Прямоугольный ACH:

AH = bcosA, CH =

CB 2 = a 2 = CH 2 + BH 2

a = .

Рис. 4

Второй способ решения задачи. Координатный метод.

1. Введём прямоугольную систему координат с началом в точке А так, чтобы точка В лежала на положительной полуоси AX, а точка С имела положительную ординату. Решение записывают все учащиеся. 2. Запишем координаты точек: B(c; 0) ; C(bcosA; bsinA). 3. Найдём квадрат стороны BC: BC 2 = a 2 = (bcosA — c) 2 + (bsinA) 2 = = b 2 cos 2 A – 2bccosA + c 2 + b 2 sin 2 A = = b 2 (cos 2 A + sin 2 A) + c 2 – 2bccosA = = b 2 + c 2 – 2bccosA. a 2 = b 2 + c 2 – 2bccosA – теорема косинусов b 2 = a 2 + c 2 – 2accosB c 2 = b 2 + a 2 – 2abcosC

Рис. 5

Вывод: Таким образом, квадрат стороны треугольника равен сумме квадратов двух других его сторон без удвоенного произведения этих сторон на косинус угла между ними.

По теореме косинусов можно найти любую сторону треугольника, зная длины двух других сторон и угол между ними.

Теорему косинусов иногда называют обобщённой теоремой Пифагора. Почему? Объясните.

Если С = 90°, то cosC = 0 и 2abcosC = 0, тогда c 2 = a 2 + b 2 .

Вывод: Теорема Пифагора является частным случаем теоремы косинусов.

Рассмотрим следствия из теоремы косинусов.

В прямоугольном ACH: bc = bcosA. Так как A – острый, то cosA > 0, тогда a 2 = b 2 + c 2 – 2bcc, то есть квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение одной из них на проекцию другой.

Случай, когда угол, лежащий против неизвестной стороны тупой рассмотреть самостоятельно. Следующий урок начнём с проверки этого задания. (т.к. cosA 2 = b 2 + c 2 + 2bccosA, т.е. квадрат стороны треугольника равен сумме квадратов двух других сторон плюс удвоенное произведение одной из них на проекцию другой.

ABC: d₁ 2 = a 2 + b 2 – 2abcosB.

ABD: d₂ 2 = a 2 + b 2 – 2abcosA = a 2 + b 2 – 2abcos(180° — B) = a 2 + b 2 + 2abcosB.

d₁ 2 + d₂ 2 = a2 + b2 – 2abcosB + a 2 + b 2 + 2abcosB = a 2 + b 2 + a 2 + b 2 .

d₁ 2 + d₂ 2 = 2 a 2 + 2 b 2 .

Вывод: Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон.

ABC,

Достроим ABC до параллелограмма ABA₁C.

AA₁ 2 + BC 2 = 2b 2 + 2c 2 . BC = a, 2m_a = AA₁.

(2m_a) 2 + a 2 = 2b 2 + 2c 2

4m_a 2 = 2(b 2 + c 2 ) – a 2

m_a 2 =

m_a =

m_b =

m_c =

Вывод: В любом треугольнике со сторонами a, b и c длины медиан m_a, m_b, m_c вычисляются по формулам: m_a = , m_b = , m_c = .

IV. Первичное осмысление и закрепление связей и отношений в объектах изучения .

Задача: В треугольнике две стороны равны 20 см и 21 см, а синус угла между ними равен 0,6. Найти третью сторону. Сколько решений имеет задача?

sin = 0,6 ,

sin = 0,6 может быть острым или тупым.

1 случай: – острый

BC 2 = AB 2 + AC 2 – 2ABACcos.

Так как – острый, то cos>0.

Тогда cos = = = = 0.8

BC = = = 13(см).

2 случай: – тупой.

BC 2 = AB 2 + AC 2 – 2ABACcos

Так как – тупой, то cos 19.02.2012

📺 Видео

Как проверяют учеников перед ЕНТСкачать

Теорема косинусов. Урок геометрии 9 класс.Скачать

Решение задачи с использованием теоремы косинусовСкачать

Теорема КосинусовСкачать

9 класс, 15 урок, Решение треугольниковСкачать

Теорема синусов и теорема косинусовСкачать

9 класс. Геометрия. Решение треугольников. Теорема косинусов. Теорема синусов. Урок #2Скачать

9 класс, 13 урок, Теорема синусовСкачать

Теорема косинусовСкачать

Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

1 следствие.
Дано: ABC Возможны 2 случая: а) A – острый, то cosA > 0, б) A – тупой, то cosA 2 = b 2 + c 2 – 2bccosA	Рис. 6
2 следствие.
Рис. 7
3 следствие.
Рис. 8
Рис. 9