Египетский треугольник свойства углы (8 видео)

Египетский треугольник

В математике есть определенные каноны, которые явились, так сказать, фундаментом или основанием всего последующего развития современной математики. Одним из этих канонов, по праву можно считать теорему Пифагора.

Кому еще со школьных времен не известна смешная формулировка теоремы Пифагора: «Пифагоровы штаны во все стороны равны». Ну да, правильно это звучит так: «квадрат гипотенузы равен сумме квадратов катетов «, но про штаны гораздо лучше запоминается.

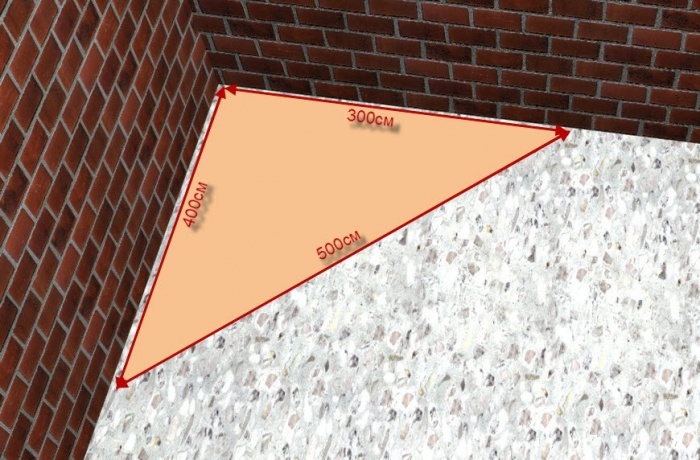
Нагляднее всего это видно на треугольнике со сторонами 3-4-5. Но если изучить внимательно использование такого треугольника в древней истории, то можно заметить одну занимательную вещь и называется она ни как по другому, как Египетский треугольник.

Этот самый философ и математик Пифагор Самосский из Греции, именем которого и названа эта теорема, жил примерно 2,5 тысяч лет тому назад. Ну конечно дошедшая до нашего времени биография Пифагора не совсем достоверна, но, тем не менее, известно что Пифагор много путешествовал по странам Востока. В том числе он был и Египте и Вавилоне. В Южной Италии Пифагор основал свою знаменитую «Пифагорову школу», которая сыграла очень даже важную роль, как в научной, так и политической жизни древней Греции. С тех времен по преданиям Плутарха, Прокла и других известных математиков того времени, считалось, что эта теорема до Пифагора известна не была и именно по этому её назвали его именем.

Но история говорит что это не так. Обратимся туда, где бывал Пифагор и что видел, прежде чем сформулировать свою теорему. Африка, Египет. Бесконечный и однообразный океан песка, почти ни какой растительности. Редкие кустики растений, едва заметные верблюжьи следы. Раскаленная пустыня. Солнце и то кажется тусклым, как будто покрытым этим вездесущим мелким песком.

И вдруг, как мираж, как видение, на горизонте возникают строгие очертания пирамид, изумительных по своим идеальным геометрическим формам, устремленным к палящему солнцу. Своими огромными размерами, и совершенством своих форм они изумляют.

Скорее всего, Пифагор их видел в ином виде, нежели как они выглядят сейчас. Это были сияющие полированные громады с четкими гранями на фоне многоколонных прилегающих храмов. Рядом с величественными царскими пирамидами стояли пирамиды поменьше: жен и родичей фараонов.

Власть фараонов Древнего Египта была непререкаемой. Фараонов считали божеством и отдавали им божественные почести. Фараон-бог был вершителем судьбы народа и его покровителем. Даже после смерти культ фараона имел преогромное значение. Умершего фараона сохраняли веками, и для сохранения тела фараона сооружали гигантские пирамиды. Величие, архитектура и размеры этих пирамид поражают и сейчас. Недаром эти сооружения относили к одному из семи чудес света.

Изначально назначение пирамид было не только как усыпальниц фараонов. Считают что они сооружались как атрибуты могущества, величия, и богатства Египта. Это памятники культуры того времени, хранилища истории страны и сведений о жизни фараона и его народа, собрание предметов быта того времени. Кроме того однозначно, что пирамиды имели определенное «научное содержание». Их ориентирование на местности, их форма, размеры и каждая деталь, каждый элемент настолько тщательно продумывались, что должны были продемонстрировать высокий уровень знаний создателей пирамид. Очевидно что они строились на тысячелетия, «навечно». И недаром арабская пословица гласит: «Все на свете страшится времени, а время страшится пирамид».

Своим аналитическим умом Пифагор не мог не заметить определенную закономерность в формах и геометрических размерах пирамид. Скорее всего, это и натолкнуло Пифагора на анализ этих размеров, что впоследствии и было им выражено своей знаменитой теоремой, от которой ныне и отталкивается современная геометия.

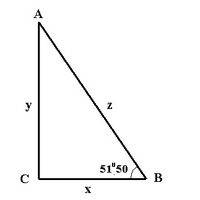
Среди множества пирамид сохранившихся до нашего времени особое место занимает пирамида Хеопса. Если рассмотреть геометрическую модель этой пирамиды и восстановить её первоначальную форму, то очевидно, что её поперечное сечение представляет собой два треугольника с внутренним углом равным 51°50′.

Сейчас пирамида является усеченной, но это разрушения времени, а если геометрически восстановить её в первоначальном виде, то получается что стороны этих треугольников равны: основание СВ = 116, 58 м, высота АС = 148,28 м.

Отношение катетов у/х = 148,28/116,58 = 1,272. А это величина тангеса угла 51град 50 мин. Получается, что в основу треугольника АСВ пирамиды Хеопса было заложено отношение AC/CB = 1,272. Такой прямоугольный треугольник называется «золотым» прямоугольным треугольником.

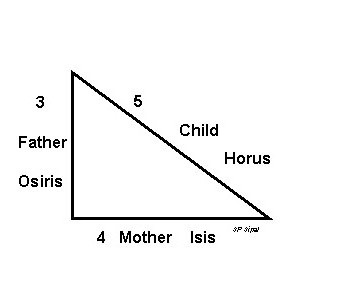
Получается что основной «геометрической идеей» пирамиды Хеопса является «золотой» прямоугольный треугольник. Но особой в этом отношении является пирамида Хефрена. Угол наклона боковых граней у этой пирамиды равен 53°12, при котором отношение катетов прямоугольного треугольника 4:3. Такой треугольник называют «священным» или «египетским» треугольником. По мнению многих известных историков, «египетскому» треугольнику в древности придавали особый магический смысл. Так Плутарх писал, что египтяне сопоставляли природу Вселенной со «священным» треугольником: символически они уподобляли вертикальный катет мужу, основание — жене, а гипотенузу — тому, что рождается от обоих.

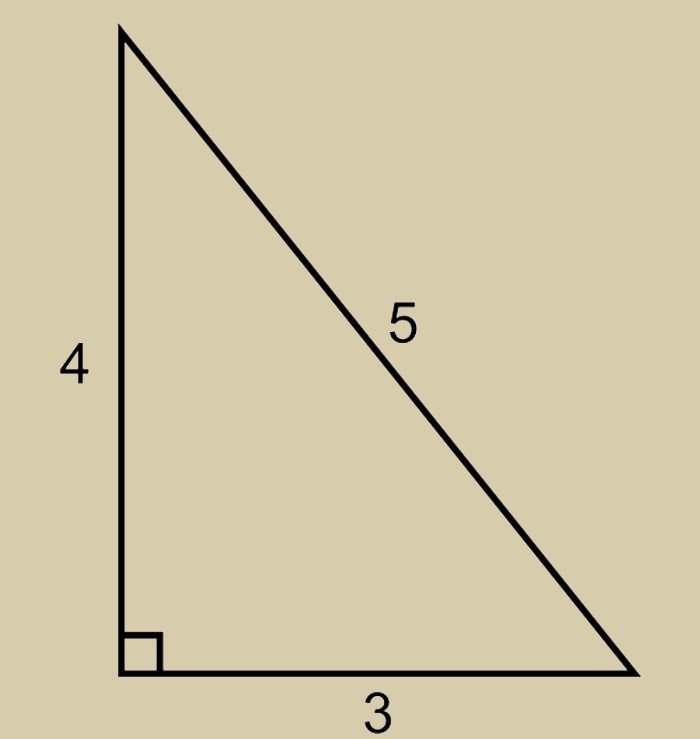
Для египетского треугольника со сторонами 3:4:5 справедливо равенство: 32 + 42 = 52, а это и есть знаменитая теорема Пифагора. По неволе напрашивается вопрос: не это ли соотношение хотели увековечить египетские жрецы, построив пирамиду в основе которой лежит треугольник 3:4:5. Пирамида Хефрена наглядное подтверждение того что знаменитая теорема была известна египтянам задолго до ее открытия Пифагором.

Неизвестно как это попало к древним египтянам, то ли это заслуга их ученых, то ли это дар из вне, не исключается и то, что это дар внеземной цивилизации, но использование такого треугольника давало египетским строителям очень существенную и к тому же простую возможность при возведении таких огромных сооружений соблюдать точные геометрические размеры. Ведь свойства этого треугольника таковы, что его угол между катетами является равный 90 градусов. То есть использование такого элемента позволяет обеспечить точную перпендикулярность сопрягаемых элементов и естественно всей конструкции, что и подтверждает архитектура древнего Египта.

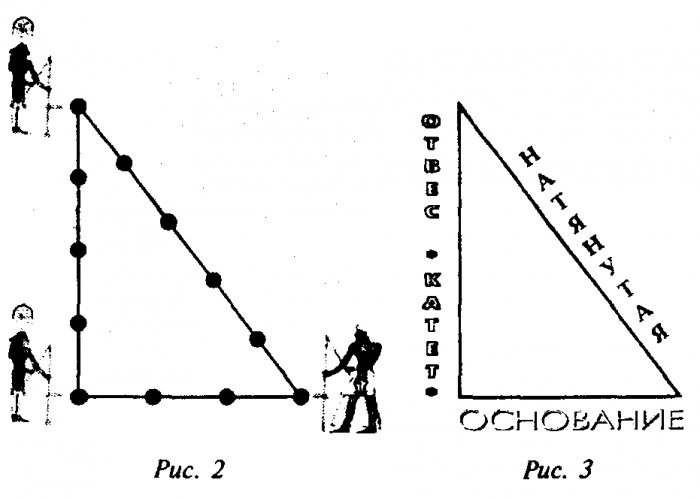
Получить прямой угол без необходимых инструментов не просто. Но если воспользоваться этим треугольником, оказывается все достаточно просто. Нужно взять обычную веревку, разделить её на 12 равных частей, и из них сложить треугольник, стороны которого будут равны 3, 4 и 5 частям. Угол между сторонами длиной 3 и 4 части оказывается и есть прямой. Вот это и есть Египетский треугольник Пифагора.

Во многих исторических письменах имеются следы, что уникальные свойства «египетского треугольника» были известны и широко использовались за много веков до Пифагора и не только в Египте, но и далеко за его пределами: в Месопотамии, в древнем Китае, в Вавилоне.

Знаменитая древнеегипетская пословица «Делай, как делается», дошедшая до наших дней, наталкивает на мысль что сами египтяне, возводившие эти строительные шедевры, были простыми исполнителями и особыми знаниями не обладали, а все секреты были скрыты от непосвященных. Ведь работами на строительстве руководили жрецы — члены особой привилегированной замкнутой касты. Они были хранителями древних знаний, которые держались в секрете. Но пытливый ум великого мыслителя Пифагора сумел разгадать один их этих секретов.

Умы людей всегда будоражат разнообразные загадки, и это, вероятно, будет всегда. Египетский треугольник, хоть и известен человечеству с незапамятных времён, все-таки одна из не полностью разгаданных тайн.

Ведь, что не говори, а форма египетского треугольника и проста, и в то же время гармонична, по своему он даже красив. И с ним достаточно легко работать. Для этого можно использовать самые простые инструменты — линейку и циркуль. Использую этот незатейливый элемент и его симметричные отображения, можно получить красивые, гармоничные фигуры. Это и мальтийский крест, и серединное сечение пирамиды Хефрена, и фрактальный ряд убывающих — возрастающих, по размерам египетских треугольников в соответствии с правилом золотого сечения. Это удивительное богатство гармоничных пропорций.

До сих пор в мире есть много пытливые люди, которые как безумцы изобретают вечный двигатель, ищут квадратуру круга, философский камень и книгу мёртвых. Скорее всего, усилия их тщетны, но даже в случае с Египетским треугольником, ясно что «простых тайн» на земле еще много.

Содержание

Египетский треугольник — загадка древности
История открытия
Применение
Доказательство
Египетский треугольник, его свойства
История египетского треугольника
Египетский треугольник в строительстве
Альтернативные способы построить прямой угол на 90 градусов
Как получить египетский треугольник при помощи верёвки
Как построить угол в 45, 30 и 60 градусов
Итоги
📽️ Видео

Видео:Египетский треугольник #огэ #математика #shortsСкачать

Египетский треугольник — загадка древности

Известный математик Пифагор совершил множество различных открытий, но большинству людей, которым не приходится регулярно сталкиваться с алгеброй и геометрией, он известен благодаря своей теореме. Ученый открыл ее, пребывая в Египте, где его очаровала красота и изящность пирамид, а это, в свою очередь, натолкнуло его на мысль о том, что в их формах прослеживается определенная закономерность.

Видео:Египетский треугольник. Пифагоровы тройки.Скачать

История открытия

Своим названием египетский треугольник обязан эллинам, которые часто посещали Египет в VII-V веках до н. э., среди них был и Пифагор. Основой пирамиды Хеопса является прямоугольный многоугольник, а

Видео:Что такое египетский треугольник?Скачать

Применение

Египетский треугольник с древности пользовался популярностью в архитектуре и строительстве.

Соотношение сторон этого треугольника 3:4:5 приводит к тому, что он является прямоугольным, т. е. один угол равен 90 градусам, а два других – 53,13 и 36,87 градусам. Прямым является угол между сторонами, соотношение которых равно 3:4.

Видео:Египетский треугольникСкачать

Доказательство

При помощи некоторых простых вычислений можно доказать, что треугольник является прямоугольным. Если следовать теореме обратной той, которую создал Пифагор, т. е. в случае, если сумма квадратов двух сторон будет равняться квадрату третьей, то он прямоугольный, а поскольку его стороны приводят к равенству 3 2 х 4 2 = 5 2 , следовательно, он является прямоугольным.
Подводя итог, надо отметить, что египетский треугольник, свойства которого уже в течение многих столетий известны человечеству, на сегодняшний день продолжает использоваться в архитектуре. Это вовсе неудивительно, ведь такой способ гарантирует точность, которая очень важна при строительстве. Кроме этого, он очень прост в использовании, что тоже значительно облегчает процесс. Все преимущества использования этого метода прошли проверку веками и остаются популярными до сих пор.

Видео:Египетский треугольник, свойстваСкачать

Египетский треугольник, его свойства

О египетском треугольнике и его свойствах хорошо известно ещё с древних времён. Эта фигура широко применялась в строительстве для разметки и построения правильных углов.

Видео:Египетский треугольникСкачать

История египетского треугольника

Создателем этой геометрической конструкции является один из величайших математиков древности Пифагор. Именно благодаря его математическим изысканиям мы можем в полной мере использовать все свойства данного геометрического построения в строительстве.

Можно предположить, что математические навыки позволили Пифагору заметить закономерность в формах строения. Дальнейшее развитие событий можно легко представить. Базовый анализ и построение выводов создали одну из самых значимых фигур в истории. Скорее всего, в качестве прообраза была выбрана именно пирамида Хеопса из-за своих практически совершенных пропорций.

Видео:Египетский треугольникСкачать

Египетский треугольник в строительстве

Свойства этой уникальной геометрической конструкции заключаются в том, что её построение без применения каких-либо инструментов позволяет построить дом с правильными во всех соотношениях углами.

Итак, качества египетского треугольника позволяют делать правильные во всех соотношениях углы. Стороны конструкции имеют следующее соотношение друг к другу:

Чтобы проверить ту ли фигуру вы начертили, используйте хорошо известную ещё со школьной скамьи Теорему Пифагора.

Для лучшего понимания возьмём приведенную выше зависимость и составим небольшой пример. Умножим пять на пять. В результате чего получим гипотенузу равную 25. Вычислим квадраты двух катетов. Они составят 16 и 9. Соответственно их сумма будет двадцать пять.

Именно поэтому свойства египетского треугольника так часто используются в строительстве. Вам достаточно взять заготовку и прочертить прямую линию. Её длина всегда должна быть кратной 5. Затем нужно наметить один край и отмерять от него линию кратную 4, а от второго 3.

Альтернативные способы построить прямой угол на 90 градусов

Как уже упоминалось выше, наилучшим вариантом будет просто взять угольник или транспортир. Эти инструменты позволяют с наименьшими затратами времени и сил добиться нужных пропорций. Главное же свойство египетского треугольника заключается в его универсальности. Фигуру можно построить, не имея в арсенале практически ничего.

Сильно в построении прямого угла помогают простые печатные издания. Возьмите любой журнал или книгу. Дело в том, что в них соотношение сторон всегда составляет ровно 90 градусов. Типографические станки работают очень точно. В противном случае рулон, который заправляется в станок, будет резаться непропорциональными кривыми углами.

Как получить египетский треугольник при помощи верёвки

Свойства этой геометрической фигуры тяжело переоценить. Неудивительно, что инженерами древности было придумано множество способов её образования с использованием минимальных ресурсов.

Одним из самых простых считается метод образования египетского треугольника со всеми его вытекающими свойствами посредством простой верёвки. Возьмите бечёвку и разрежьте её на 12 абсолютно ровных частей. Из них сложите фигуру с пропорциями 3, 4 и 5.

Как построить угол в 45, 30 и 60 градусов

Безусловно, египетский треугольник и его свойства очень полезны при постройке дома. Но без других углов вам обойтись всё-таки не удастся. Чтобы получить угол, равняющийся 45 градусам, возьмите материал рамки или багета. После чего распилите его под углом в сорок пять градусов и состыкуйте половинки друг с другом.

Как видите, свойства фигуры позволяют гораздо проще и быстрее построить геометрический конструкт. Чтобы добиться соотношения сторон в 60 градусов нужно взять один треугольник на 30º и второй такой же. Обычно подобные пропорции необходимы при создании определённых декоративных элементов.

Видео:Равнобедренный треугольник. Свойства равнобедренного треугольника | Математика | TutorOnlineСкачать

Итоги

Свойства египетского треугольника широко использовались в строительстве на протяжении почти, что двух с половиной веков. Даже сейчас при недостатке инструментов строители применяют эту открытую ещё Пифагором методику, чтобы добиться ровных прямых углов.