Свойства тензоров второго ранга эквивалентны свойствам квадратной матрицы , построенной из компонент тензора.
Тензор второго ранга называется симметричным, если для любых индексов i и j выполняется равенство: .
Тензор второго ранга называется антисимметричным, если для любых индексов i и j выполняется равенство: .
Произвольный тензор второго ранга можно представить в виде суммы симметричного и антисимметричного тензоров:
Вектор называется собственным вектором симметричной квадратной матрицы , а — ее собственным значением, если выполняется условие:
В тензорной алгебре направление, задаваемое вектором называется главным направлением тензора , а -главным значением тензора.
Система уравнений, из которой находятся главные направления и главные значения тензора является системой линейных, однородных уравнений относительно компонент вектора , которая имеет отличное от нуля решение только при условии :
где — единичная матрица. Раскрывая определитель, получаем для нахождения главных (собственных) значений тензора алгебраическое уравнение третьей степени (т.е. кубическое уравнение).
Можно доказать, что в случае симметричного тензора полученное уравнение всегда имеет три вещественных корня. Возможно, что некоторые из них, совпадают по величине. (В этом случае корни называются кратными или вырожденными.) Если все корни различны, каждому из них однозначно соответствуют направления в пространстве, называемые главными направлениями тензора. В случае вырожденных корней возникает неоднозначность в выборе главных направлений. Так в случае двукратного вырождения корня существует плоскость, проходящая через начало координат, перпендикулярная третьему главному направлению, все направления на которой являются главными. Если вырождение трехкратное, то любые направления в пространстве являются главными. Аналогично, в случае тензоров на плоскости (двумерное пространство) возможны либо два разных вещественных корня, либо эти корни совпадут.
В согласии со сказанным, главные направления (главные оси) симметрического тензора второго ранга всегда можно выбрать взаимно ортогональными. Эти направления выбираются однозначно в случае невырожденных главных значений и неоднозначно в случае вырождения. В системе главных осей тензор диагонален, а на его главной диагонали стоят главные (собственные) значения.
(Следует иметь в виду, что в данном случае суммирование по индексу i не подразумевается).
Для геометрической иллюстрации указанных свойств симметричного тензора второго ранга удобно ввести понятие характеристической поверхности тензора. Ее уравнение имеет вид уравнения, определяющего поверхность второго порядка:
Если все главные значения тензора одинаковы , то такой тензор называется шаровым. Шаровой тензор пропорционален единичному и имеет одинаковый вид во всех системах координат. Характеристическая поверхность шарового тензора есть сфера. Если два главных значения одинаковы, а третье отлично от них , то тензор называется симметрическим. Его характеристическая поверхность является поверхностью вращения. Если все три собственные значения различны, то такой тензор называется асимметрическим, а его характеристическая поверхность является поверхностью второго порядка общего вида.
Если все главные значения тензора положительны, то тензор называется положительно определенным. Если все главные значения отрицательны, то тензор называется отрицательно определенным. В этих случаях при построении характеристических поверхностей надо выбирать разные знаки в правой части уравнения поверхности (плюс для положительно определенного тензора и минус для отрицательно определенного). И в том, и в другом случаях характеристическая поверхность тензора есть эллипсоид (шар в случае , эллипсоид вращения в случае и эллипсоид общего вида в случае ).
Если некоторые собственные значения тензора положительны, а некоторые отрицательны, то тензор называется знаконеопределенным. Его характеристической поверхностью является гиперболоид с двумя листами, отвечающим двум знакам в правой части уравнения для характеристической поверхности.
Для вычисления собственных значений симметричного тензора второго ранга в трехмерном пространстве удобно воспользоваться следующим приемом. Преобразуем уравнение, определяющее собственные значения
Замена переменной приводит к кубическому уравнению относительно величины , в котором отсутствует квадратичный член. (Удобно обозначить коэффициенты нового уравнения как -3p и 2q. В случае трех вещественных корней величина p > 0)
Корни этого уравнения могут быть найдены по формуле:


Ее доказательство основано на использовании известного выражения для синуса тройного аргумента: . Запишем данное выражение как тождество: . Сделав в кубическом уравнении замену , получим , или . Сравнение данного уравнения с тригонометрическим тождеством позволяет найти все его корни как , где . Отсюда следует, что и соответственно: , где n=1,2,3. (Конец доказательства).
Собственные векторы симметрического тензора , принадлежащие собственному значению , находим как , где — миноры матрицы с данным собственным значением .
- 4.1 Разложить в двумерном случае тензор второго ранга на сумму симметричного и антисимметричного тензоров. Компоненты тензора равны:
- 4.1.1
- 4.1.2
- 4.1.3
- 4.1.4
- 4.1.5
- 4.1.6
- 4.2 Разложить тензор второго ранга на сумму симметричного и антисимметричного тензоров, где равны
- 4.2.14.2 .2
Решение задачи 4.2.1. Используем для данного разложения формулы: и . Непосредственное вычисление компонент симметричного и антисимметричного тензоров дает: , , и т.д.
- 4.3 Для симметричного тензора на плоскости:
- 4.3.1 Найти собственные значения.
- 4.3.2 Найти собственные векторы.
- 4.3.3 Проверить ортогональность собственных векторов.
- 4.3.4 Найти орты системы координат, связанной с главными осями.
- 4.3.5 Записать матрицу поворота к главным осям.
- 4.3.6 Записать вид тензора в главных осях.
- 4.3.7 Построить характеристическую поверхность.
Произвести вычисления для тензоров с компонентами:
- а)
- б)
- в)
- г)
- 4.4 Разложить тензор на сумму симметричного и антисимметричного тензоров. Для симметричного тензора :
- 4.4.1 Найти собственные значения.
- 4.4.2 Найти собственные векторы.
- 4.4.3 Проверить ортогональность собственных векторов
- 4.4.4 Найти орты системы координат, связанной с главными осями.
- 4.4.5 Записать матрицу поворота к главным осям.
- 4.4.6 Записать вид тензора в главных осях.
- 4.4.7 Классифицировать тензор (шаровой, симметрический, асимметрический, положительно, отрицательно определенный или знаконеопределенный).
Произвести вычисления для тензоров с компонентами:

Решение задачи 4.4.1(а) Симметричная часть указанного тензора
Раскрыв определитель, получим . Нахождение корней этого уравнения , , решает поставленную задачу.
Решение задачи 4.4.2(а) Проведем вычисление компонент собственного вектора, принадлежащего собственному значению . Для этого следует решить уравнение . Подставив , распишем его как систему трех линейных уравнений . Отсюда следует, что , . (Здесь — любое вещественное число, не равное нулю)
Аналогично, для находим , . И, наконец, для компоненты собственного вектора , .
Решение задачи 4.4.4(а) Используем найденные выше три собственных вектора , , , принадлежащих соответственно собственным значениям 2, 5, 10. Орты системы координат, связанной с главными осями тензора, по определению, это собственные векторы с модулями, равными единице. Очевидно, что при , , собственные векторы имеют единичные модули. Поэтому, искомые орты имеют вид: , ,


Решение задачи 4.4.5(а) Искомая матрица поворота , здесь -орты системы главных осей тензора, -орты системы координат, в которой заданы компоненты тензора. Учитывая, что , , вычислим все возможные скалярные произведения . В итоге мы получим матрицу поворота , по строкам которой расположены компоненты орт системы главных осей тензора. Как у любой матрицы поворота ее определитель равен 1. В ряде случаев возможен результат (-1). Тогда, для построения матрицы поворота требуется дополнительно изменить направление одного из орт.
Решение задачи 4.4.6(а) Выполним поворот в систему главных осей тензора. Его компоненты в повернутой системе координат вычисляются как матричное произведение . Воспользуемся матрицей поворота, найденной в ходе решения предыдущей задачи, и вычислим матричное произведение
В системе главных осей тензор диагонален, а на его главной диагонали расположены главные (собственные) значения.
4.5 Какая характеристическая поверхность отвечает тензору, у которого одна (две) главных значения равны 0?
Видео:Собственные векторы и собственные числа линейного оператораСкачать

Собственные значения и собственные векторы матрицы
Собственные значения и собственные векторы матрицы
С задачами на собственные значения инженер сталкивается в самых различных ситуациях. Так для тензоров (матриц) напряжений собственные значения определяют главные напряжения, а собственные векторы задают направления нормалей к главным сечениям. При динамическом анализе механических систем собственные значения соответствуют собственным частотам колебаний. Инженер должен стараться сделать собственные частоты проектируемого им сооружения отличными от тех, которые могут вызываться внешними воздействиями (ветром, автотранспортом и т. д.). Вообще, собственные частоты колебаний являются наиболее важной характеристикой практически любой динамической системы.
Опр. Число λ и ненулевой вектор X называется собственным значением и соответствующим ему собственным вектором квадратной матрицы А, если выполняется соотношение

Некоторые свойства собственных значений и собственных векторов
1. У квадратной матрицы размерности n существует ровно n не обязательно различных собственных значений.
2. Все собственные значения вещественной симметричной матрицы вещественны.
3. Собственные векторы вещественной симметричной матрицы, соответствующие различным собственным значениям, ортогональны, то есть их скалярное произведение равно нулю.
4. Если X – собственный вектор матрицы A, то вектор 

5. Сумма всех собственных значений матрицы А равна сумме ее диагональных элементов

6. Произведение всех собственных значений матрицы А равно ее определителю

Нахождение собственных значений и собственных векторов матрицы
По определению собственных значений и собственных векторов матрицы имеем


Соотношение (3) представляет собой однородную систему линейных алгебраических уравнений. В развернутом виде она выглядит так

СЛАУ (3) всегда имеет нулевое решение, которое нам не подходит. Если ее определитель не равен нулю, то нулевое решение является единственным. Ненулевое решение, которое нас интересует в соответствии с (1), существует только, если определитель СЛАУ (3) равен нулю. Поэтому будем иметь

Если раскрыть определи, то получим алгебраическое уравнение n-го порядка относительно 
Использование матриц при исследовании
напряженного состояния тел
Плоское напряженное состояние
Плоское напряженное состояние описывается тремя компонентами напряжений 


которая называется матрицей (тензором) напряжений. Так как 
Напряжения в произвольном сечении






l и m представляют собой проекции единичного вектора 



Подставим (1) и (3) в (2)


Формулы (5) известны из курса сопротивления материалов и могут быть получены из уравнений равновесия статики для сил, действующих на элементарную призму.
Найдем нормальное 

Так как 

Здесь 

Для нахождения касательного напряжения спроектируем вектор напряжения 


Подставим (9) в (8)

Формулы (7), (10) выводятся в курсе сопротивления материалов из уравнений равновесия статики. Преимущество соотношений (2), (6) и (8) в том, что они справедливы как для плоского, так и для объемного напряженных состояний.
Нахождение главных напряжений и положения главных сечений
Так как на главных сечениях касательное напряжение τ равно нулю и вектор напряжений 

где σ – нормальное напряжение на главном сечении, то есть главное напряжение. Подставляя (2) в (11), найдем

Отсюда с учетом, что 
Для нахождения главных напряжений составим характеристическое уравнение для матрицы ∑ и решим его

Найдем теперь положение главного сечения, на котором действует главной напряжение 




Так как определитель системы линейных алгебраических уравнений (14) равен нулю, то ее уравнения линейно зависимы и одно из них следует отбросить, заменив условием, что длина вектора 


Из (15) 


Аналогично находятся 

Видео:Собственные векторы и собственные значения матрицыСкачать

Главные оси и главные значения тензора
Видео:Собственные значения и собственные векторы матрицы (4)Скачать

Главные направления и главные значения.
Как отмечалось ранее, определена операция умножения тензора V на вектор а, результатом которой является новый вектор Ъ : Va = Ь. Эту операцию мы определяли как действие тензора на вектор, приводящее в общем случае к изменению его длины и направления. Интерес представляет такое направление а, для которого действие тензора сводится только к изменению длины вектора (но нс направления!). Если выполняется соотношение
то направление вектора а называют главным направлением тензора (или главной осью тензора), а скаляр Л — главным значением тензора. В теории квадратных матриц эквивалентом этих характеристик являются собственные вектора и соответствующие им собственные числа. Как мы увидим в дальнейшем, тензор может иметь несколько главных направлений и соответствующих им главных значений.
Покажем, что при переходе в другую координатную систему с помощью ортогонального преобразования главное значение и главное направление сохраняются. Для этого умножим соотношение (1.17) слева на ортогональную матриц>’ преобразования координат И 7 , а между сомножителями V и а вставим единичную матрицу ? = = W T W. Пользуясь ассоциативным законом, выполним приведенную ниже цепочку преобразований Va = Ха —* WV(W T W)a = = XWa —? (WV(V T )(Wa) = A(Wa) —» V’a’ = Ха из которой следует независимость Л и а от выбора координатной системы. Следовательно, главные направления и главные значения являются особыми характеристиками тензора, независимыми от выбора координатной системы, в которой в данный момент этот тензор рассматривается. Как мы увидим в дальнейшем, главные оси и главные значения играют очень важную роль в тензорном исчислении, поэтому ключевым является вопрос их нахождения для заданного тензора.
Определение главных значений тензора. Очевидно, условие существования главных значений и направлений Va — Ха = 0 приводится к системе линейных однородных уравнений (V — Х?)а = О, которая в подробной записи будет иметь вид
Как известно, однородная линейная система, кроме тривиального (нулевого) решения, может иметь при определенных условиях и ненулевое, так называемое нетривиальное решение. Компоненты этого решения могут быть определены лишь с точностью до произвольного множителя (т.е. могут быть определены лишь их отношения, выражающие направление в пространстве вектора а). Поэтому длину вектора а нормируют так, чтобы его модуль был равен единице и он указывал особое направление в пространстве — главное направление тензора. По аналогии с теорией матриц этот вектор можно назвать собственными вектором матрицы тензора, а главное значение тензора представится собственными числом его матрицы, отвечающим данному собственному вектору.
Для существования нетривиального решения необходимо потребовать равенства нулю основного определителя системы (1.18):
Раскрывая определитель (1.19), получим кубическое уравнение относительно главного значения:
которое в подробной записи будет иметь вид
Оно называется характеристическим уравнением или иногда — ве- ковыл1 уравнением для данного тензора. Коэффициенты этого уравнения определяются компонентами тензора. Уравнение (1.20) может иметь три действительных корня или один действительный и два комплексно-сопряженных. Возможен также случай кратных корней.
В соответствующих разделах теории матриц доказывается, что для симметрической матрицы (симметрического тензора) все корни характеристического уравнения (1.20) являются действительными числалш. В дальнейшем мы часто будем пользоваться этим свойством, гак как большинство рассматриваемых тензорных объектов или симметрические, или из них естественным образом выделяется симметрическая часть.
Инварианты симметрического тензора. Ранее мы показали, что главные значения тензора сохраняются при переходе к другой координатной системе — инвариантны относительно преобразования вращения. Здесь мы подходим к важному понятию инвариантов тензора. Инвариантами тензора называются такие функции его компонентов, которые сохраняют свою величину при переходе в другую координатную систему. Понятие инвариантов определено в общем случае для тензоров любого ранга. Так, скаляр тензор нулевого ранга является инвариантом. Для вектора тензора первого ранга — инвариантом является квадрат его длины. Для тензора второго ранга имеется более богатый набор инвариантов, который характеризует данный тензорный объект и определяет его фундаментальные характеристики.
Из того, что корни характеристического уравнения не зависят от выбора системы координат, можно получить систему инвариантов тензора, которая широко используется в различных приложениях тензорного исчисления. Так как коэффициенты алгебраического уравнения выражаются, согласно теореме Виста, через его корни, то коэффициенты (1.20) будут инвариантны к выбору системы координат. Таким образом для афинного ортогонального тензора второго ранга мы можем в качестве инвариантов принять коэффициенты 1, /2 и /3 его характеристического уравнения:
Первый инвариант выражает то свойство, что в любой системе координат сумма диагональных элементов тензора есть величина постоянная:
Второй инвариант тензора можно также определить с помощью операции взятия следа:
Из трех приведенных инвариантов можно получить бесчисленное множество других. Так, например, в задачах прочности часто используется комплекс
Так как он является алгебраической функцией инвариантов, то и сам будет инвариантом. Таким образом можно построить произвольное количество инвариантов, в частности систему инвариантов, называемых моментами, на основе вычисления следов степеней тензора:
Инварианты тензора 1, /2 и /3 , определенные как коэффициенты характеристического уравнения (1.20), называются главнылш инвариантами.
Инварианты можно построить и для объектов более высокой мерности. Так, главными инвариантами матрицы А порядка п называются коэффициенты U ее характеристического многочлена
Девиатор и шаровой тензор. Тензор, у которого первый инвариант равен нулю, называется deeuamopoAi, а диагональный тензор, у которого все диагональные компоненты одинаковы С = к?, — шаровыми тензором. При переходе к другим координатным системам шаровые и девиаторные свойства тензоров сохраняются.
Часто произвольный тензорный объект представляют в виде суммы дсвиаторной и шаровой составляющих:
Такое представление соответствует физическому расщеплению некоторого явления на более удобные в описании и понимании составляющие. При исследовании напряженного состояния упругой среды выделение дивиаторной части означает устранение из рассмотрения процессов объемного сжатия, в то время как шаровая часть именно этим процессам и отвечает.
Видно, что девиатор характеризуется лишь двумя инвариантами, а все инварианты шарового тензора выражаются через значение его диагонального компонента: 1 = ЗЛт, /2 = ЗА; 2 , /3 = кг. В определенном смысле можно полагать что шаровой тензор представляет отображение скалярной величины на класс тензорных объектов. Такой характеристикой является, например, гидростатическое давление в жидкости, которое можно сопоставить с шаровой частью тензора напряжений стоксовской вязкой жидкости.
Теорема представления симметрических тензоров. Для симметрических тензоров имеет место теорема представления, согласно которой любая изотропная скалярная функция, аргументом которой является симметрический тензор, может быть представлена как функция трех главных инвариантов этого тензора: / = f(V) =
Взаимосвязь между соосными тензорами. Можно показать, что тензор удовлетворяет своему характеристическому уравнению
Это известная теорема матричного исчисления — теорема Гамильтона Кэли, которая справедлива и для характеристических уравнений квадратных матриц более высокого порядка. Из этого соотношения можно сделать важное заключение о характере взаимосвязи между соосными тензорами. Такие связи часто формулируются при построении более сложных моделей механики сплошных сред.
Прежде всего установим некоторые свойства степеней тензоров. Покажем, что любая степень тензора V» имеет гот же набор собственных векторов, что и сам тензор V. Для доказательства этого утверждения умножим выражение, определяющее собственный вектор тензора Vv = v, слева на тензор Т. Получим V(Vv) = V(Xv) или, после очевидных преобразований, V 2 v = X 2 v.
Таким образом, главные направления у тензоров V 2 и V совпадают, а главные значения тензора V 2 являются квадратами главных значений тензора V.
Тензоры, главные направления которых совпадают, называются соосными. Последовательное применение приведенного выше преобразования показывает соосность всех степеней исходного тензора. Можно сказать, что степени тензора образуют соосное семейство. Заметим также, что как умножение матриц тензора на скаляр, гак и добавление к сумме степеней шарового тензора нс изменяют собственных векторов (оставляют главные направления неизменными).
Предположим теперь, что между тензорами А и В существует аналитическая зависимость
причем, коэффициенты этой зависимости являются в общем случае скалярной функцией от инвариантов тензора В .’
В силу теоремы Гамильтона Кэли мы можем из (1.21) выразить третью степень тензора через низшие:
Подставляя в (1.22) представление высших степеней тензора в соответствии с соотношением (1.23), мы сможем понизить степени всех членов, начиная с третьей до второй. Окончательно взаимосвязь между тензорами представится в виде
где коэффициенты , с’2, с’> являются скалярными функциями инвариантов матрицы тензора В.
📺 Видео
Собственные векторы и собственные числа линейного оператораСкачать

Собственные векторы и собственные значенияСкачать

Собственные значения и собственные векторыСкачать

Собственные значения и собственные векторы. ТемаСкачать

7 4 Собственные векторы и собственные значенияСкачать

А.7.35 Собственные вектора и собственные значения матрицыСкачать

Квантовая механика 8 - Операторы. Собственные векторы и собственные значения.Скачать

Айгенвектора и айгензначения | Сущность Линейной Алгебры, глава 10Скачать

Собственные значения и собственные векторы. ПримерСкачать

Овчинников А. В. - Линейная алгебра - Собственные значения и собственные векторы линейного оператораСкачать

Практика 1. Часть 1. Собственные вектора и значения линейного оператора. Канонический вид.Скачать

А.7.40 Метод Якоби поиска собственных векторов и значений симметричных матрицСкачать

Косимов А Собственные векторы и собственные значенияСкачать

Собственные значения матрицыСкачать

Алгебра и геометрия 1. Собственные значения, вектора и подпространстваСкачать

Привести квадратичную форму к каноническому видуСкачать
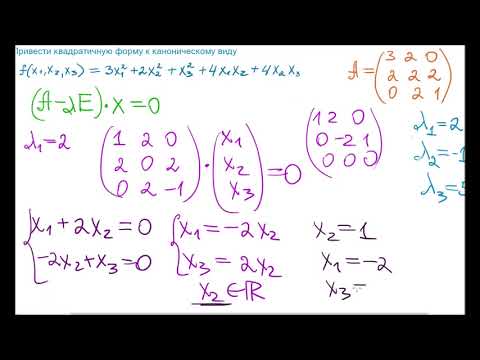
Вычислительные методы алгебры - Степенной метод, метод вращенийСкачать











































































