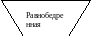Четырехугольники на каждом шагу проект (2 видео)

Урок-проект «Четырехугольники». 8-й класс

Класс: 8

Содержание

Презентация к уроку
«Мир четырёхугольников»
Просмотр содержимого документа «»Мир четырёхугольников»»
Проект по математике на тему «Четырехугольники на каждом шагу» (8 класс)
«Управление общеобразовательной организацией: новые тенденции и современные технологии»
📹 Видео

Презентация к уроку

Тип урока: открытия нового знания (исследовательский).

Цели урока:

Образовательная: дать определения и вывести особые свойства прямоугольника, ромба, квадрата.
Развивающая: развитие математического и общего кругозора, мышления и речи, формирование умений применять приемы наблюдения, сравнения, анализа сформировать навыки исследовательской деятельности.
Воспитательная: воспитать ответственное отношение к учебе, воспитание воли и настойчивости для достижения конечных результатов.

Методы и приемы: Исследовательская работа в группах при изучении теоретического материала.

Технология обучения: Технология проблемного обучения, деятельностный подход в обучении.

Форма организации труда: Работа по группам 3-х уровней: повышенный, средний, обязательный

Оборудование: карточки с заданиями, слайды для устной работы, опорные конспекты с теоретическим материалом, компьютер, проектор, интерактивная доска.

Структура урока:

Устная разминка.
Постановка целей.
Исследовательская работа по трем блокам. А. Прямоугольник. В. Ромб. С. Квадрат.
Практическая работа.
Защита проекта. Работа по опорному конспекту.
Закрепление.
Информация о домашнем задании.
Итоги урока.

Ожидаемые результаты:

Учащиеся должны знать: определение и свойства параллелограмма, прямоугольника, ромба, квадрата.
Учащиеся должны уметь: применять свойства параллелограмма для доказательства свойств ромба, квадрата, прямоугольника.

Этап урока (время)

Деятельность учителя

Деятельность учащихся1. Организационный момент (1 мин.)

Цель: формирование познавательной компетентности– Сегодня мы продолжим изучение темы «Четырехугольники».
Одной из основных и простейших фигур в геометрии является четырехугольник.
За несколько тысячелетий геометры так подробно изучили четырехугольник, что иногда говорят о «геометрии четырехугольника» как о самостоятельном разделе геометрии.Правила работы на уроке: работаем по группам, оценивается лично и по группам2. Актуализации опорных знаний (8 мин.)

Цель: повторение и обсуждение заданий, необходимых при изучении новой темыУстные задания: Слайды 3, 4, 5Общеклассная2. «Открытие» детьми нового знания (8 мин.)

Цель: формирование продуктивной творческой компетентности 1. Открытие «нового знания»– На какие две группы вы бы разбили данные четырехугольники?

– А теперь из предложенных параллелограммов выберем те, которые:

1) содержат прямые углы
2) имеют равные стороны
3) имеют равные стороны и прямые углы

Слайды 8-12Групповая работа

Какова тема нашего урока?

Даем определение каждому четырехугольнику3. Постановка проблемы– Можем ли сейчас решить задачу? Нет.

– Почему не можем решить задачу? Не знаем, по-видимому, каких-то особых свойств данных четырехугольников.

– Мы приступили к исследованию темы урока, Сегодня нам предстоит сыграть роль исследователей и открыть особые свойства четырехугольников.
Всего у нас три блока. Каждая группа выбирает один из блоков и выполняет задание.

– Ну а теперь приступаем к заданию, выдвигаем гипотезу и доказываем ее.

Видео:Четырехугольники. Геометрия 8 класс.Скачать

«Мир четырёхугольников»

Проектная работа учащихся 8 класса. В ней представлен материал, который изучается на уроке и вне урока.

Просмотр содержимого документа
«»Мир четырёхугольников»»

Районный конкурс ученических

проектов по математике

Муниципальное бюджетное общеобразовательное учреждение Жирятинская средняя общеобразовательная школа им.А.Ф.Возликова

Молодожен Лидия Сёмина Анастасия

Руководитель :Козлова Галина Петровна, учитель математики

с.Жирятино ул.Ленина д.38

2.1 Определение четырехугольника ………………… 4

2.2 Таблица классификации четырёхугольников……5…

2.8 Ортодиагональный четырёхугольник…………………

I. Введение Актуальность темы: Нам порою кажется, что геометрия совершенно не связана с нашей жизнью, что это очень трудная и совсем непонятная наука. Часто самые интересные факты — из-за малого количества отведенных на предмет часов — проходят мимо вас. На самом же деле мы с вами живем в мире, который неразрывно связан с геометрией. В ходе работы над проектом перед нами открылся удивительный мир четырёхугольников, обладающих неповторимыми свойствами. Квадраты, ромбы, прямоугольники… каждый ученик сталкивается с ними в школе на уроках геометрии. Основополагающий вопрос: Можно ли представить себе мир без четырехугольников? Зачем мы изучаем четырехугольники? Какое применение находят четырехугольники в природе и технике? Что связывает четырехугольники между собой? Чем интересны четырехугольники? Научная формулировка гласит, что геометрия — это раздел математики, который изучает фигуры и свойства фигур на плоскости и в пространстве . Стоит осмотреться, и мы увидим, что многие предметы имеют форму, похожую на уже знакомые нам геометрические фигуры. В современной архитектуре смело используются самые разные геометрические формы, чаще всего – четырехугольники. Плитки пола в ванной, на тротуарах, на вокзалах чаще бывают четырехугольными. По улице движутся автомобили, автобусы, троллейбусы, их окна это четырехугольники: трапеции, квадраты, прямоугольники. Цель работы – Провести классификацию четырехугольников, систематизировать знания для подробного изучения темы «Четырехугольники»; уметь применять теоретические знания в решении практических, занимательных задач, активизировать познавательную деятельность и интерес к геометрии.

Исходя из цели, были поставлены следующие задачи:

1. Рассмотреть определения четырехугольников .

2. Изучить виды, свойства, признаки четырехугольников.

3. Выяснить, в каких областях человеческой деятельности применяются четырехугольники.

Объект исследования: геометрические фигуры четырехугольники.

Методы исследования:

изучение дополнительной литературы по данному вопросу;
наблюдения в повседневной жизни;

Обобщение и систематизация изученного материала .

2. Основное содержание

2.1 Определение четырехугольника.

Четырёхугольником называется фигура, которая состоит из четырёх точек (вершин) и четырёх отрезков (сторон), которые последовательно соединяют вершины. При этом никакие три из данных точек не должны лежать на одной прямой, а соединяющие их отрезки не должны пересекаться. Каждый четырехугольник имеет четыре вершины, четыре стороны и две диагонали. [1,19]. В курсе геометрии мы изучали выпуклые многоугольники: Параллелограмм, Ромб, Прямоугольник, Квадрат, Трапецию.

2.2 Таблица классификации четырёхугольников

В ажнее всех фигур,

Я всех их свойствами своими наделил.

Хоть стороны мои попарно и равны, и параллельны,

Всё ж я в печали, что не равны мои диагонали,

Да и углы не делят пополам.

Параллелограмм – четырёхугольник, у которого противолежащие стороны попарно параллельны.

1.Противоположные стороны параллелограмма равны и противоположные углы равны.

2.Диагонали параллелограмма точкой пересечения делятся пополам.

Если в четырёхугольнике две стороны равны и параллельны, то этот четырёхугольник – параллелограмм

Если в четырехугольнике две стороны попарно равны, то этот четырехугольник – параллелограмм.

Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник – параллелограмм. [1,15].

Сумма любых двух соседних углов параллелограмма равна 180°:

Каждая диагональ делит параллелограмм на два равных треугольника. [4,7].

А я — особый параллелограмм,

В се стороны мои наклонены,

да и к тому же все равны.

Меня за это ромбом величают.

Геометрической фигурой называют.

Диагонали под прямым углом пройдут.

На части равные фигуру разобьют.

Ромб – параллелограмм, у которого все стороны равны. Ромб является параллелограммом, значит, он обладает всеми свойствами параллелограмма.

Диагонали ромба взаимно перпендикулярны и делят его углы пополам, т.е. диагонали ромба пересекаются под прямым углом и являются биссектрисами его углов.

1) Если у параллелограмма диагонали взаимно перпендикулярны, то он является ромбом.

2) Если диагональ параллелограмма является биссектрисой его углов, то он является ромбом.

3) Если у четырехугольника все стороны равны, то он является ромбом.

4) Если смежные стороны параллелограмма равны, то он является ромбом.

2.5 Прямоугольник A я — прямоугольник,

В отличие от всех.

Все стороны свои держу я строго,

Две — чуть поменьше, ну а две побольше,

Которые напротив — те равны,

А те, что смежные, углом прямым скрепляю,

И преимущество имею я:

«Ведь всё ж равны мои диагонали».

Прямоугольником называется параллелограмм, у которого все углы прямые.

Диагонали прямоугольника равны

Признак: Если в параллелограмме диагонали равны, то этот параллелограмм — прямоугольник.

Р екомендуюсь: я — квадрат.

Любую площадь я измерить рад.

С глубокой древности я — мера площадей,

Она в квадрате стороны моей.

Имею я четыре стороны,

И все они равны.

Но у меня притом равны диагонали,

Углы они мне делят пополам,

На части равные разбит я ими сам.

Вобрав всё важное в себя,

Фигурой знатной стал и я

Квадрат – это прямоугольник, у которого все стороны равны.

Свойства: Квадрат обладает всеми свойствами ромба и прямоугольника.

1.Все углы квадрата прямые.

2.Диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся полам, делят углы квадрата пополам.

А я — фигура, не похожая на всех

. Хоть я и не параллелограмм, Но среди всех фигур мне место есть.

Ведь у меня же параллельны основания.

Бывают стороны равны, диагонали.

Ещё углы при основании.

Тогда трапецией я равнобедренной зовусь.

Трапецией называется четырёхугольник, у которого две стороны параллельны, а две стороны не параллельны.

Параллельные стороны трапеции называются основаниями, а две другие – боковыми. Высота трапеции – перпендикуляр, проведённый из произвольной точки одного основания трапеции к прямой, содержащей другое основание трапеции.

Средней линией (первой средней линией) трапеции называется отрезок, который соединяет середины боковых сторон данной трапеции: Средняя линия трапеции параллельна её основаниям и равна их полусумме.

У равнобокой трапеции:

углы при основании равны:

сумма противолежащих углов равна 180

Трапеция называется прямоугольной, если одна из её боковых сторон перпендикулярна основаниям.

2.8 Ортодиагональный четырёхугольник

Изучая дополнительную литературу мы выяснили, что существуют другие виды четырёхугольников

Ортодиагональный четырёхугольник — это четырёхугольник, в котором диагонали пересекаются под прямым углом.

. Согласно описанию этих четырёхугольников, два красных квадрата на двух противоположных сторонах четырёхугольника дают в сумме ту же площадь, что и два синих квадрата на другой паре сторон.

Дельтоид является ортодиагональным четырёхугольником, в котором одна диагональ является осью симметрии. Дельтоиды — это в точности ортодиагональные четырёхугольники, имеющие окружность, касающуюся всех четырёх сторон. Таким образом, дельтоиды являются описанными ортодиагональными четырёхугольниками[1].

Ромб — это ортодиагональный четырёхугольник с двумя парами параллельных сторон

2.8 Практическое применение четырехугольников в решении реальных задач.

Работая над проектом, мы нашли интересные факты о некоторых четырёхугольниках

Французский математик Франсуа Лукас (1847-1891)- специалист в области теории чисел, занимаясь поиском простого объяснения формы арабских цифр, столкнулся с легендой о перстне царя Соломона.

Легенда гласит, что на драгоценном камне, украшавшем перстень, была изображена таинственная фигура, квадрат с двумя диагоналями, из которой, можно получить фигуры всех десяти цифр

В средние века и в эпоху Возрождения математики были заворожены числом 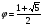= 1.61803398. названным «божественной пропорцией». Среди фигур — «золотой прямоугольник»..(В нём отношение большей стороны к меньшей равно числу 1.618

Демонстрация этой фигуры и её свойств:

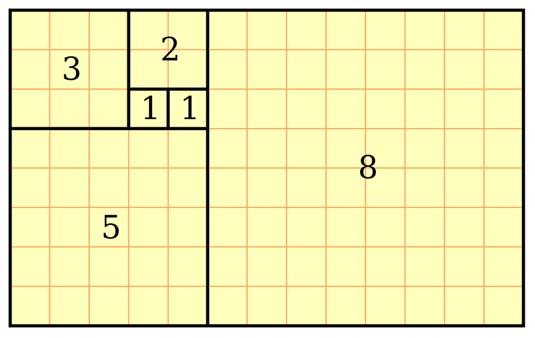
Золотой прямоугольник сечения делится на квадрат и другой, меньший золотой прямоугольник сечения. Этот процесс может быть продолжен до бесконечности, добавляя квадрат (площадь) по более длинной стороне золотого прямоугольника сечения.

Окна, рамы картин, здания, книги часто приблизительно соответствуют Золотому прямоугольнику.

Парфенон V в. до н.э. одно из красивейших сооружений древнегреческой архитектуры.

Правило золотого сечения просматривается в фасаде здания.

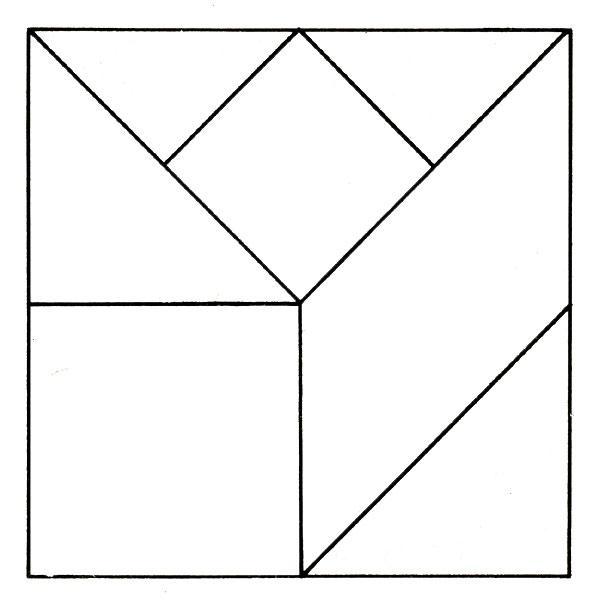
4.Занимательная игра «Пифагор» Чтобы дать пищу нашему мозгу, человек издавна изобретает различные занимательные игры. Давайте рассмотрим некоторые математические игры. Вот, например, китайская игра «Танграм», она же греческая игра «стомахион». У нас можно встретить игру «Пифагор».

Ими увлекались ещё Архимед, французский император Наполеон.

Описание игры. Квадрат размером 7X7 см разрезан так, что получается 7 геометрических фигур: 2 разных по размеру квадрата, 2 маленьких треугольника, 2 — больших (в сравнении с маленькими) и 1 четырехугольник (параллелограмм).

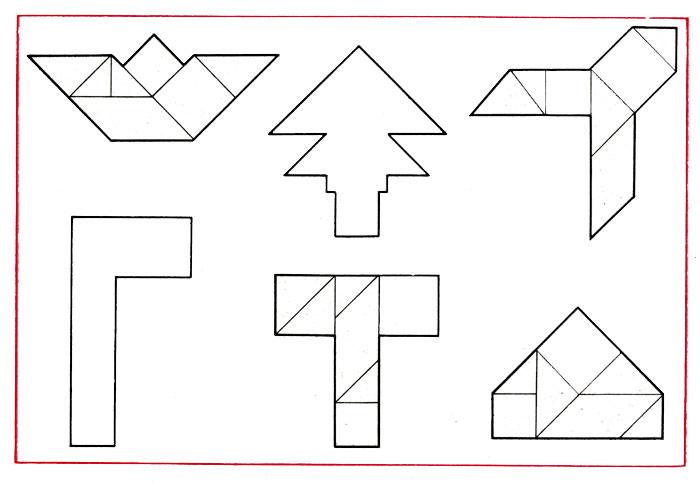
Цель игры состоит в составлении из 7 геометрических фигур — частей игры, плоских изображений: силуэтов строений, предметов, животных.

Работая над проектом, наблюдая за окружающим миром мы выяснили, что четырехугольники окружают нас повсюду и играют важную роль в нашей жизни: определяют форму столь необходимых нам предметов, приборов и механизмов, радуют глаз, красуясь на фасадах памятников архитектуры и исторических сооружений, помогают в построении планов и схем, делают наш быт и повседневность проще, легче и удобней.

Вывод: Четырёхугольники – просто, сложно, интересно!

5.Список использованных источников

http://ru.wikipedia.org – Википедия – свободная энциклопедия

http://www.nigma.ru – интеллектуальная поисковая система

Атанасян Л.С. Геометрия 7-9: учеб. Для общеобразоват. Учреждений – М.: Просвещение, 2013

Большая энциклопедия Кирилла и Мефодия – 2010

Глейзер Г.И. «История математики»

9. Энциклопедия. Я познаю мир. Математика. – М.: ООО «Издательство АСТ», 2003. – 408 с.

Видео:Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

Проект по математике на тему «Четырехугольники на каждом шагу» (8 класс)

Видео:3 правила для вписанного четырехугольника #shortsСкачать

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»

Свидетельство и скидка на обучение каждому участнику

МБОУ СОШ № 71 г. Воронеж

Проект по математике в 8 классе по теме:

Подготовила учитель математики ВКК

1. Развитие умения применять математические знания по теме в практической деятельности человека.

1. Систематизировать сведения о четырёхугольниках и их свойствах.

2. Развивать интерес учащихся к математике через занимательные игры.

В процессе работы над проектом были созданы по интересам и склонностям группы учащихся разных направлений.

Избрали лидеров групп, определили роли каждого члена группы

Каждая группа получила задание.

Сообщения об истории возникновения некоторых математических терминов. Малоизвестная информация из истории изучения свойств четырёхугольника.

Карточки для работы с классом.

Сообщение: «Свойства четырёхугольника»

Сообщение о приложении геометрии в геодезии.

Изготовленные приборы: экер, «параллельные линейки», шарнирные фигуры «прямогольник-параллелограмм», «треугольник», «трапеция».

Модели чашечных весов Роберваля, макет колёс тепловоза.

Сообщить и показать приёмы в работе столяра.

Сообщить и показать приёмы в работе швеи. Рисунки.

Провести психологический тест в классе и проанализировать результат.

информацию об истории возникновения игр «Танграм», «Оригами» и продемонстрировать правила игры.

Учитель: «Основоположник геометрии Евклид сказал: «В математике нет особых путей для королей». Мы сейчас пройдём многовековой путь в геометрии: от возникновения некоторых математических понятий до использования их в наши дни. А помогут нам ребята из учебных микрогрупп, которые приготовили об этом свои сообщения на основе проведенных исследований.

II . Обмен информацией

1-й ученик: Нам нужно было выяснить происхождение терминов «Параллелограмм», «Ромб», «Трапеция». Мы узнали, что в древних египетских и вавилонских математических документах встречаются следующие фигуры: квадраты и прямоугольники, равнобедренный и прямоугольный треугольники. Термин «параллелограмм» происходит от греческих слов «параллелос» — тот, что идёт рядом, и «грамме» — черта, линия. Согласно Проклу (создатель первого каталога геометрических терминов, в 5 в.н.э.), термин был введен Евклидом. Слово «ромб» греческого происхождения, в древности оно означало вращающееся тело, веретено. «Трапеция» — греческое слово, означавшее в древности «столик». Древнегреческий математик Фалес (6 в. до н.э.) открывает свойства квадрата и прямоугольника и применяет их в решении практических задач: измеряет высоту громадной пирамиды, измеряет расстояние от берега до корабля, находящегося в море.

2-й ученик: Мы подготовили задание классу.

Задание классу: Как можно получить фигуры всех десяти цифр?

Эксперимент: Вам предлагается набор прямоугольников. Выберите тот, который вам больше нравится.

Экспериментаторы определили, что люди находят соотношение 1,618 эстетически приятным.

«Никакое человеческое исследование не может называться настоящим знанием, если оно не прошло через математическое доказательство», — считал Леонардо да Винчи.

В средние века и в эпоху Возрождения математики были заворожены числом = 1.61803398. названным «божественной пропорцией». Один из крупных математиков эпохи Возрождения Лука Пачоли издал в 1509г. трактат «О божественной пропорции» с иллюстрациями Леонардо да Винчи. Трактат содержит интересные примеры, в которых встречаются такие отношения. Среди фигур — «золотой прямоугольник», у которого отношение сторон равно j».

Демонстрация этой фигуры и её свойств:

Окна, рамы картин, здания, книги часто приблизительно соответствуют Золотому прямоугольнику.

Парфенон V в. до н.э. одно из красивейших сооружений древнегреческой архитектуры.

Правило золотого сечения просматривается в фасаде здания. Ученые установили, что в Парфеноне нет прямых линий, а поверхности не плоские, а слегка изогнутые. Зодчие знали, что строго горизонтальная линия или плоская поверхность кажется наблюдателю слегка изогнутой посередине.

Учитель: «Математику уже затем учить надо она ум в порядок приводит», — всем известно это выражение М. В. Ломоносова».

Упорядочим знания о четырёхугольниках и мы.

2.2. Микрогруппа «теоретики».

«Круги Эйлера»: учащиеся рассказывают о свойствах фигур

Микрогруппа «Теоретики» выявляет четырехугольники в «Кругах Эйлера»

Вдумаемся в слова известных людей о приложении теории к решению практических задач: «Рано или поздно всякая правильная математическая идея находит применение в том или ином деле». (А.Н.Крылов).

«Измеряй всё, что можешь измерить, и делай таковым всё, не поддающееся измерению». (Ф.Бэкон). Эти слова подтвердят «геодезисты».

2.3. Микрогруппа «геодезисты».

Задача 1: Две доступные точки А и В разделены препятствиями. Найдите расстояние между ними.

Найдите расстояния между недоступными точками А и В.

Учитель: Помощь геодезистам в работе на местности окажут ребята из «конструкторского бюро».

2.4. Микрогруппа «Конструкторское бюро»

Демонстрация изготовленных приборов.

1) Прибор «экер» для построения на местности прямых углов и «провешивания».

2) Прибор «Параллельные линейки». Рассказ ученика, на чём основано это устройство и о его использовании.

3)Шарнирные «прямоугольник-параллелограмм», «треугольник», трапеция».

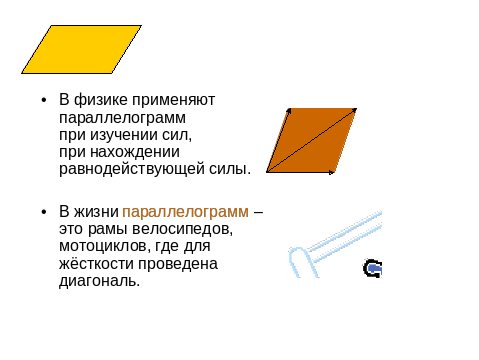
Учащийся демонстрируют «жёсткость» фигур и объясняет

их применение в жизни.

4-й ученик Применение шарнирного соединения параллелограмма.

Чашечные весы Роберваля.

Шарнирный параллелограмм опирается на подставках в точках М и N . Мы всегда имеем параллельность сторон АВ и С D .

5-й ученик Демонстрация макета колёс тепловоза и их работы.

Стержень АВ, длина которого равна расстоянию ОО₁ между центрами колёс, передает движение от одного колеса к другому.

2.5. Микрогруппа «столяры».

Решение практических задач с теоретическим обоснованием:

Как проверить правильность изготовления рамы?

Как разделить доску с параллельными краями по длине на полосы равной ширины?

Как плотник может отрезать конец доски с параллельными краями под углом 45 о ?

Какие углы должны иметь ромбовидные плитки, чтобы ими можно было выложить паркетный пол?

Столяр, желая проверить, имеет ли поверхность стола форму квадрата, измеряет его стороны и находит, что они равны. Все ли операции он выполнил?

Как проверить, что выпиленный из фанеры четырёхугольник есть квадрат, располагая остальной частью фанеры?

« В математике есть своя красота, как в живописи и поэзии»,- утверждает известный ученый Н.Е.Жуковский..

2.6 Красоту четырёхугольников в моделях продемонстрируют девочки из микрогруппы «Швея».

Демонстрация моделей одежды (в рисунках) с использованием элементов отделки в виде ромбов, прямоугольников, квадратов.

Практические приёмы выкройки «квадрата», «ромба».

Задача: Как проверить, что отрезанный кусок материи — квадрат

— Грек Пифагор (6в. до н.э.) провозгласил: «Числа правят миром».Так ли это, сейчас помогут разобраться учащиеся из группы «Психологи».

2.7. Микрогруппа «Психологи».

Что по Пифагору означало «4»?

«Число «4» Пифагор и его ученики изображали «справедливость». Первыми четырьмя числами 1, 2, 3 и 4 они обозначали четыре элемента, из которых, по воззрениям древнегреческих мудрецов, состоял весь мир: огонь, землю, воду и воздух.

2-й ученик Эксперимент (работа с классом):

Взгляните на следующие фигуры:

Выберите из них ту, в отношении которой можете сказать: «Это — я!» Постарайтесь почувствовать свою форму. Если вы испытываете сильное затруднение, выберите из фигур ту, которая первой привлекла вас.

Краткие психологические характеристики соответствующих форм личности

Если вашей основной фигурой оказался квадрат, то вы — неутомимый труженик. Трудолюбие, усердие, потребность доводить начатое дело до конца, упорство, позволяющее добиваться завершения работы, — вот основные качества истинных Квадратов. Выносливость, терпение и методичность обычно делают Квадрата высококлассным специалистом в своей области. Все сведения, которыми они располагают, систематизированы и разложены по полочкам. Квадрат способен выдать необходимую информацию моментально. Поэтому Квадраты заслуженно слывут эрудитами. Квадратам быстро устанавливать контакты с разными лицами

Эта форма символизирует лидерство. Самая характерная особенность истинного Треугольника — способность концентрироваться на главной цели. Они — энергичные, сильные личности. Треугольник — это очень уверенный человек, который хочет быть правым во всем! Треугольники быстро и успешно учатся (впитывают полезную информацию как губка). Треугольники честолюбивы

Это люди, не удовлетворенные тем образом жизни, который они ведут сейчас, и поэтому занятые поисками лучшего положения. У Прямоугольника обнаруживаются позитивные качества, привлекающие к нему окружающих: любознательность, пытливость, живой интерес ко всему происходящему и. смелость! Правда, оборотной стороной этого является чрезмерная доверчивость, внушаемость.

Круг — самая доброжелательная из пяти форм. Круги «болеют» за свой коллектив и популярны среди коллег по работе. Пытаясь сохранить мир, они иногда избегают занимать «твердую» позицию и принимать непопулярные решения. В одном Круги проявляют завидную твердость — если дело касается вопросов морали или нарушения справедливости.

Зигзаги обычно имеют развитое эстетическое чувство. Зигзаги — идеалисты, отсюда берут начало такие их черты, как непрактичность, наивность. Зигзаг — самый возбудимый из пяти фигур. Они несдержанны, очень экспрессивны, используя свое природное остроумие, они могут быть весьма язвительными, «открывая глаза» другим.

Учитель: «Старайся дать уму как можно больше пищи», призывал великий русский писатель Л. Толстой.

2.8. Микрогруппа «Эврика».

1-й ученик Чтобы дать пищу нашему мозгу, человек издавна изобретает различные занимательные игры. Давайте рассмотрим некоторые математические игры. Вот, например, китайская игра «Танграм», она же греческая игра «стомахион». У нас можно встретить игру «Пифагор».

Ими увлекались ещё Архимед, французский император Наполеон.

Рассказ об игре и демонстрация рисунков, которые можно выполнить из 7 частей квадрата.

«Сотни фигур из 7 частей»

2-й ученик. Демонстрирует им изготовленную игру «Пифагор».

3-й ученик. Древнеяпонская игра «оригами»:

Квадратный лист бумаги, который можно только сгибать, преображается в рыб, птиц и животных.

(Обоснование математической стороны этой игры).

III . Подведение итогов работы.

Учитель: «Жизнь лишь постольку прекрасна, поскольку её можно посвятить изучению математики и её преподаванию», — писал известный ученый Б.Паскаль. Обоснуйте справедливость этого суждения.