Четырехугольник вписан в окружность так что его вершины делят окружность в отношении 3 5

Геометрия | 5 — 9 классы

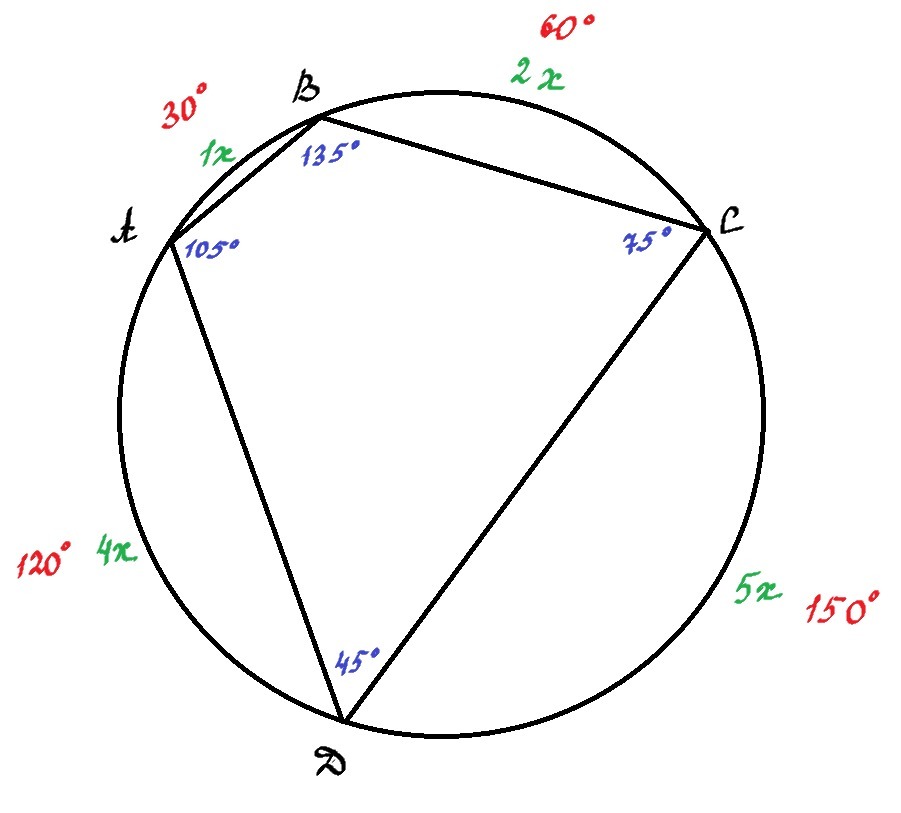
Вершины четырёхугольника ABCD делят окружность в отношении 1 : 2 : 5 : 4.

Найдите углы этого четырёхугольника.

Смотри рисунок к задаче в прикрепленном файле.

Вершины четырехугольника делят окружность на дуги.

Обозначим одну часть через х°.

Тогда градусная мера дуги АВ = х, дуги ВС = 2х, дуги CD = 5х, дуги DA = 4х.

В сумме все эти дуги дают 360°х + 2х + 5х + 4х = 36012х = 360х = 30.

Значит дуга АВ 30°, дуга ВС 2 * 30° = 60°, дуга CD = 5 * 30° = 150°, дуга DA 4 * 30° = 120°.

Градусная мера вписанного угла равна половине градусной меры дуги, на которую он опирается.

Угол А опирается на дугу ВD.

ВD = ВС + CD = 60° + 150° = 210°.

∠А = 210° : 2 = 105°Угол В опирается на дугу АС.

АС = СD + DA = 150° + 120° = 270°∠В = 270° : 2 = 135°.

Угол С опирается на дугу DB.

DB = DA + AB = 120° + 30° = 150°∠С = 150° : 2 = 75°.

∠D = 360° — (105° + 135° + 75°) = 45°.

Ответ : ∠А = 105°, ∠В = 135°, ∠С = 75°, ∠D = 45°.

Видео:Четырехугольники, вписанные в окружность. 9 класс.Скачать

Вершины четырёхугольника ABCD лежат на окружности?

Вершины четырёхугольника ABCD лежат на окружности.

Верно ли, что угол ACD = углу ABD?

Видео:3 правила для вписанного четырехугольника #shortsСкачать

Вершины четырёхугольника делят окружность в отношении 1 : 2 : 5 : 4?

Вершины четырёхугольника делят окружность в отношении 1 : 2 : 5 : 4.

Найдите углы этого четырехугольника.

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Угол A четырёхугольника ABCD, вписанного в окружность, равен 80 градусов?

Угол A четырёхугольника ABCD, вписанного в окружность, равен 80 градусов.

Найдите угол C этого четырёхугольника.

Ответ дайте в градусах.

Видео:ОГЭ ЗАДАНИЕ 16 ЧЕТЫРЕХУГОЛЬНИК АВСД ВПИСАН В ОКРУЖНОСТЬ. НАЙДИТЕ УГОЛ АБДСкачать

Вершины четырехугольника abcd делят окружность в отношении 1 : 2 : 8 : 7 ?

Вершины четырехугольника abcd делят окружность в отношении 1 : 2 : 8 : 7 .

Найдите углы этого четырехугольника.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

В выпуклом четырёхугольнике ABCD диагонали пересекаются и точкой пересечения делятся пополам?

В выпуклом четырёхугольнике ABCD диагонали пересекаются и точкой пересечения делятся пополам.

Найдите больший угол четырёхугольника, если угол А : угол В = 2 : 4.

Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Окружность вписана в четырёхугольник ABCD?

Окружность вписана в четырёхугольник ABCD.

Известно что AD = 12 ; BC = 18.

Найдите периметр ABCD.

Видео:Четырехугольник АВСD со сторонами АВ=12 иСD=13 вписан в окружность. 27 вариант Ященко ОГЭ задача 25Скачать

Углы A, B и C четырёхугольник ABCD относятся как 7 : 3 : 11?

Углы A, B и C четырёхугольник ABCD относятся как 7 : 3 : 11.

Найдите угол D, если около данного четырёхугольника можно описать окружность.

Видео:Четырёхугольник ABCD со сторонами AB = 40 и CD = 10 вписан в окружность. Диагонали #огэ #математикаСкачать

Вершины четырёхугольника ABCD лежат на окружности и разделяют её на четыре дуги, градусные меры которых относительно как 3 : 7 : 5 : 3 Найдите больший угол четырёхугольника?

Вершины четырёхугольника ABCD лежат на окружности и разделяют её на четыре дуги, градусные меры которых относительно как 3 : 7 : 5 : 3 Найдите больший угол четырёхугольника.

Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

СРОЧНО?

Найдите углы А и В четырёхугольника ABCD, вписанного в окружность, если угол С = 12, а угол D = 118 градусам.

Видео:Вписанный в окружность четырёхугольник.Скачать

Углы А, В, С четырёхугольника АВСD, вписанного в окружность, относятся как 3 : 2 : 7?

Углы А, В, С четырёхугольника АВСD, вписанного в окружность, относятся как 3 : 2 : 7.

Найдите больший угол этого четырёхугольника (в градусах).

Перед вами страница с вопросом Вершины четырёхугольника ABCD делят окружность в отношении 1 : 2 : 5 : 4?, который относится к категории Геометрия. Уровень сложности соответствует учебной программе для учащихся 5 — 9 классов. Здесь вы найдете не только правильный ответ, но и сможете ознакомиться с вариантами пользователей, а также обсудить тему и выбрать подходящую версию. Если среди найденных ответов не окажется варианта, полностью раскрывающего тему, воспользуйтесь «умным поиском», который откроет все похожие ответы, или создайте собственный вопрос, нажав кнопку в верхней части страницы.

60гр, 120гр, 60гр, 120гр. Используйте свойство внешнего угла треугольника и сумму острых углов прямоугольного треугольника. Ответ : 60, 120, 60, 120 градусов.

По идее 180 — 80 = 100 100 : 2 = 50 Ответ : 2 парралельных угла по 50 градусов.

Первое задание там совподают CA — AC лучи.

Периметр сумма всех сторон, многоугольник это ломанная у которой много углов.

Дано : O — центр окружностиAB = 4 смCM — AM = 4 смНайти : r (радиус окружности)Решение : CM = CO + OM = r + OMAM = OA — OM = r — OMCM — AM = 4r + OM — r + OM = 42×OM = 4OM = 2 ⇒ CM = r + 2, AM = r — 2Рассмотрим ΔMBA — прямоугольныйПо теореме Пифагора..

Ответ : r = 4 смОбъяснение : Дано : АС — диаметр окружности, точка В лежит на окружности, ВМ⊥АС, СМ = АМ + 4. Найти : r. Решение : Рисунок к задаче смотри в прикрепленном файле. Пусть АМ = х, тогда МС = х + 4. ΔАВМ прямоугольный, т. К. ВМ⊥АС (по..

Через точкуNможно провести бесконечное множество прямых, если известно, чтоN∉a.

Если все боковые ребра пирамиды равны, то вершина пирамиды проецируется в центр окружности описанной около основания. В основании прямоугольный треуг — к, значит центр окружности является серединой гипотенузы. Рассмотрим основание пирамиды треуг — ..

Видео:Описанная и вписанная окружности четырехугольника - 8 класс геометрияСкачать

Вписанный четырехугольник в окружность. Четырехугольник ABCD вписан в окружность

С разделением математики на алгебру и геометрию учебный материал становится сложнее. Появляются новые фигуры и их частные случаи. Для того чтобы хорошо разобраться в материале, необходимо изучить понятия, свойства объектов и сопутствующие теоремы.

Видео:11 класс, 43 урок, Вписанный четырехугольникСкачать

Общие понятия

Под четырехугольником подразумевается геометрическая фигура. Состоит она из 4-х точек. Причем 3 из них не располагаются на одной прямой. Имеются отрезки, последовательно соединяющие указанные точки.

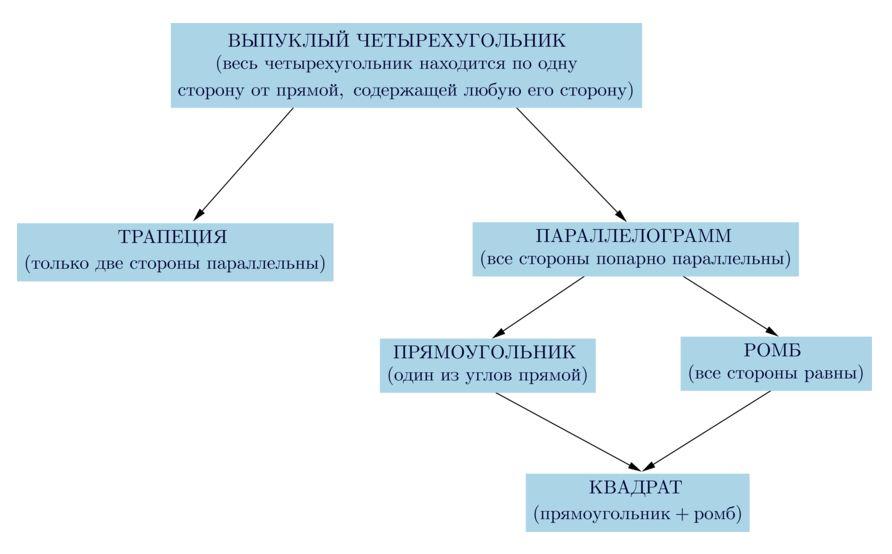
Все четырехугольники, изучаемые в школьном курсе геометрии, показаны в следующей схеме. Вывод: любой объект из представленного рисунка обладает свойствами предыдущей фигуры.

Вам будет интересно: Железнодорожный техникум в Челябинске после 9 класса: специальности, отзывы

Четырехугольник может быть следующих видов:

• Параллелограмм. Параллельность его противоположных сторон доказывается соответствующими теоремами.
• Трапеция. Четырехугольник, у которого основания параллельны. Другие две стороны – нет.
• Прямоугольник. Фигура, у которой все 4 угла = 90º.
• Ромб. Фигура, у которой все стороны равны.
• Квадрат. Совмещает в себя свойства последних двух фигур. У него все стороны равны и все углы прямые.

Основное определение данной темы – вписанный четырехугольник в окружность. Оно заключается в следующем. Это фигура, вокруг которой описана окружность. Она должна проходить через все вершины. Внутренние углы четырехугольника, вписанного в окружность, в сумме дают 360º.

Не каждый четырехугольник может быть вписан. Связано это с тем, что серединные перпендикуляры 4-х сторон могут не пересечься в одной точке. Это сделает невозможным нахождение центра окружности, описанной около 4-угольника.

Видео:ОПИСАННЫЕ И ВПИСАННЫЕ ОКРУЖНОСТИ ЧЕТЫРЕХУГОЛЬНИКА . §10 геометрия 8 классСкачать

Частные случаи

Из всякого правила есть исключения. Так, в данной теме также имеются частные случаи:

• Параллелограмм, как таковой, не может быть вписан в окружность. Только его частный случай. Это прямоугольник.
• Если все вершины ромба находятся на описывающей линии, то он является квадратом.
• Все вершины трапеции находятся на границе окружности. В таком случае говорят о равнобедренной фигуре.

Видео:Урок 2. Описанная окружность около четырехугольника. Задача из ОГЭ| Подобные треугольникиСкачать

Свойства вписанного четырехугольника в окружность

Перед решением простых и сложных задач по заданной теме необходимо удостовериться в своих знаниях. Без изучения учебного материала невозможно решить ни один пример.

Видео:ЕГЭ Математика Задание 6#27935Скачать

Теорема 1

Сумма противоположных углов, четырехугольника вписанного в окружность, равна 180º.

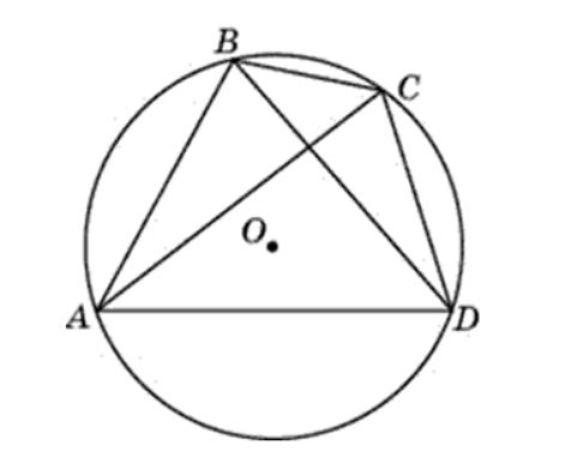
Дано: четырехугольник АВСД вписан в окружность. Ее центр – точка О. Нужно доказать, что

Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Вписанный четырехугольник. Задание 6

Вписанный четырехугольник. Задание 6

При решении задач на нахождение углов вписанного четырехугольника нам нужно вспомнить, что

1. Четырехугольник называется вписанным в окружность, если все его вершины лежат на окружности:

2. Сумма противоположных углов вписанного четырехугольника равна 180°:

Рассмотрим решение задач из Открытого банка заданий по математике:

1 .Задание B7 (№ 27871)

Угол A четырехугольника ABCD, вписанного в окружность, равен 58°. Найдите угол C этого четырехугольника. Ответ дайте в градусах.

Сумма углов А и С равна 180°, поэтому угол С равен 180°-58°=122°

Ответ: 122°

2 . Задание B7 (№ 27927)

Два угла вписанного в окружность четырехугольника равны 82° и 58°. Найдите больший из оставшихся углов. Ответ дайте в градусах.

Углы 82° и 58° не могут быть противоположными, так как их сумма не равна 180°. Значит, оставшиеся углы являются противоположными к этим. очевидно. что величина большего угла равна 180°-58°=122°

3 . Задание B7 (№ 27928)

Углы A, B и C четырехугольника ABCD относятся как 1:2:3. Найдите угол D, если около данного четырехугольника можно описать окружность. Ответ дайте в градусах.

Введем единичный угол. Тогда величины углов А, В и С можно записать так:

А=х, В=2х, С=3х. Суммы противоположных углов вписанного четырехугольника равны и равны 180°. Сумма углов А и С равна 4х и равна 180°. Отсюда х=45°.

Очевидно, что величина угла D равна 4х-2х=90°

📸 Видео

Вписанная и описанная окружность - от bezbotvyСкачать

8 класс Геометрия. Окружность вписанная в четырехугольник и описанная около четырехугольника Урок #4Скачать

Четырёхугольник ABCD вписан в окружность ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

16 задание из ОГЭ| Четырехугольник ABCD вписан в окружность, ABC = 105°, CAD = 29°, найдите угол ABDСкачать