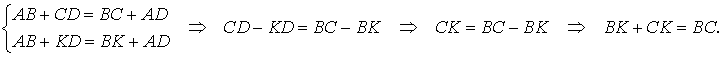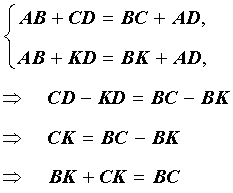Четырехугольник klmn описан около окружности с центром о

Четырехугольник KLMN описан около окружности и вписан в окружность. Прямые KL и NM пересекаются в точке P. Найдите площадь треугольника KPN, если известно, что ∠KPN = φ и радиусы окружностей, вписанных в треугольники KPN и LMP равны соответственно r и R.

Решение . Первый случай.

Центры O₁ и O окружностей, вписанных в треугольники KPN и LMP соответственно, лежат на биссектрисе PO угла KPN. Окружность, вписанная в четырехугольник KLMN, является также окружностью, вписанной в треугольник KPN и вневписанной окружностью треугольника LMP.

Четырехугольник KLMN вписан в окружность, следовательно, ∠LKN + ∠LMN = 180°. Но ∠LMP + ∠LMN = 180°, откуда ∠LKN = ∠LMP. Так как треугольники KPN и LMP имеют еще общий угол KPN, они подобны, причем коэффициент подобия равен отношению радиусов окружностей, вписанных в эти треугольники.

1)

2) S_ΔLPM = pR, где p — полупериметр треугольника LPM равный длине отрезка AP, как сумма отрезков касательных проведенных из одной точки.

3) из прямоугольного треугольника OAP находим откуда

Подставляя найденное S_ΔLPM в формулу площади треугольника KPN, окончательно получаем

Отличается от первого расположением точки P левее точек N и K. В этом случае R > r и в рассуждении они и треугольники LMP и KPN должны быть поменяны местами. Таким образом, в этом случае KPN — меньший из двух треугольников, а радиус вписанной в него окружности r. Значит

S_KPN = rp, где p — полупериметр треугольника KPN равный отрезку PB. При этом, как и в первом случае, Таким образом,

Ответ: или

Четырёхугольник ABCD описан около окружности, с центром в точке О. Докажите, что сумма градусных мер углов: a)AOB и COD; 6)BOC и AOD равна 180°.

Ваш ответ

Похожие вопросы

• Все категории
• экономические 43,277
• гуманитарные 33,618
• юридические 17,900
• школьный раздел 606,688
• разное 16,822

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Описанные четырехугольники

Определение 1 . Окружностью, вписанной в четырёхугольник, называют окружность, которая касается касается каждой из сторон четырёхугольника (рис.1). В этом случае четырёхугольник называют четырёхугольником, описанным около окружности или описанным четырёхугольником .

Замечание . В настоящем разделе мы рассматриваем только выпуклые четырёхугольники.

Теорема 1 . Если четырёхугольник описан около окружности, то суммы длин его противоположных сторон равны.

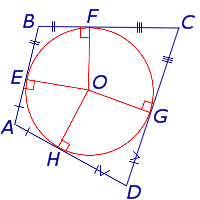
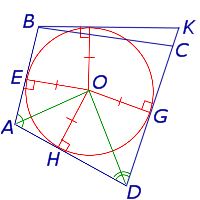
Доказательство . Рассмотрим четырёхугольник ABCD , описанный около окружности, и обозначим буквами E, F, G, H – точки касания сторон четырёхугольника с окружностью (рис.2).

AH = AE, BF = BE, CF = CG, DH = DG,

Складывая эти равенства, получим:

AH + BF + CF + DH =
= AD + BC,
AE + BE + CG + DG =
= AB + CD,

то справедливо равенство

что и требовалось доказать.

Теорема 2 (обратная теорема к теореме 1) . Если у четырёхугольника суммы длин противоположных сторон равны, то в этот четырёхугольник можно вписать окружность.

Доказательство . Рассмотрим четырёхугольник ABCD , длины сторон которого удовлетворяют равенству

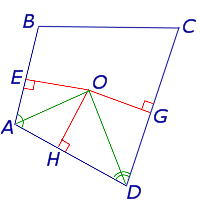
и проведём биссектрисы углов BAD и CDA . Обозначим точку пересечения этих биссектрис буквой O , и опустим из точки O перпендикуляры OH, OE и OG на стороны AD, AB и CD соответственно (рис.3).

Следовательно, справедливы равенства

из которых вытекает, что точки H, E и G лежат на окружности с центром в точке O и радиусом OH , касающейся сторон четырёхугольника AD, AB и CD в точках H, E и G соответственно. При этом возможны два случая:

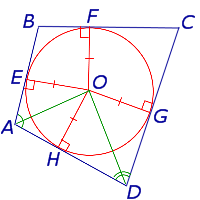
Окружность касается касается стороны BC (рис.4).

В этом случае четырёхугольник ABCD описан около окружности, и теорема доказана.

Окружность не касается стороны BC .

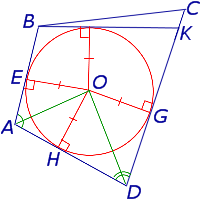
В этом случае касательная, проведенная к окружности из точки B , пересекает прямую DC в точке K , и возможны два случая:

Точка K лежит между точками C и D (рис.5)

Рассмотрим случай 2а и приведём его к противоречию. В этом случае в силу того, что четырёхугольник ABKD является описанным, а также по условию теоремы справедливы равенства:

Последнее равенство утверждает, что в треугольнике BKC сумма двух сторон равна третьей стороне, что противоречит неравенству треугольника неравенству треугольника неравенству треугольника . Полученное противоречие доказывает, что случай 2а невозможен.

Совершенно аналогичные рассуждения позволяют заключить, что случай 2b также невозможен.

Итак, возможен и реализуется лишь случай 1.

Из доказательства теоремы 2 непосредственно вытекает

Теорема 3 . Биссектрисы всех внутренних углов описанного четырёхугольника пересекаются в одной точке – центре вписанной окружности.

В следующей таблице приводятся примеры четырёхугольников, в которые можно вписать окружность. Доказательства утверждений непосредственно вытекают из теорем 1 и 2 и предоставляются читателю в качестве несложных упражнений.

Примеры описанных четырёхугольников

Фигура	Рисунок	Утверждение
Ромб		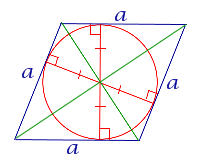В любой ромб можно вписать окружность
Квадрат		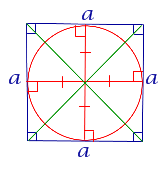В любой квадрат можно вписать окружность
Прямоугольник		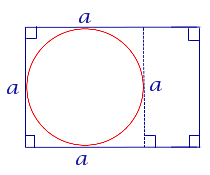В прямоугольник можно вписать окружность тогда и только тогда, когда он является квадратом
Параллелограмм		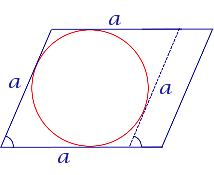В параллелограмм можно вписать окружность тогда и только тогда, когда он является ромбом
Дельтоид		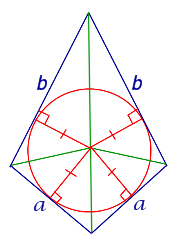В любой дельтоид можно вписать окружность
Трапеция		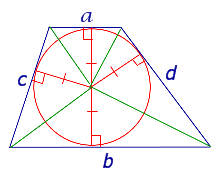В трапецию можно вписать окружность тогда и только тогда, когда у трапеции сумма длин боковых сторон рана сумме длин оснований

Ромб

Квадрат

В любой квадрат можно вписать окружность

Прямоугольник

В прямоугольник можно вписать окружность тогда и только тогда, когда он является квадратом

Параллелограмм

В параллелограмм можно вписать окружность тогда и только тогда, когда он является ромбом

Дельтоид

Трапеция

В трапецию можно вписать окружность тогда и только тогда, когда у трапеции сумма длин боковых сторон рана сумме длин оснований

🎦 Видео