В правильной четырехугольной пирамиде MABCD с вершиной M стороны основания равны 15, а боковые ребра равны 16.
а) Докажите, что прямые MC и BD перпендикулярны.
б) Найдите площадь сечения пирамиды плоскостью, проходящей через точку B и середину ребра MD параллельно прямой AC.
а) Спроецируем прямую MC на плоскость ABCD, проекцией будет являться прямая AC. Однако диагонали квадрата перпендикулярны, поэтому . А тогда, по теореме о трех перпендикулярах,
.
б) Пусть точка E — середина ребра MD. Отрезок BE пересекает плоскость MAC в точке P. В треугольнике MBD точка Р является точкой пересечения медиан, следовательно, MP:РО = 2 : 1, где O — центр основания пирамиды. Отрезок FG параллелен AC и проходит через точку P (точка F принадлежит ребру MA, G — ребру MC), откуда
Четырёхугольник BFEG — искомое сечение. Отрезок BE — медиана треугольника MBD, значит,
Поскольку прямая BD перпендикулярна плоскости MAC, диагонали BE и FG четырёхугольника BFEG перпендикулярны, следовательно,
Ответ:
Видео:СЕЧЕНИЯ. СТРАШНЫЙ УРОК | Математика | TutorOnlineСкачать

С2 (№16) на нахождение площади сечения пирамиды
В новом формате ЕГЭ по математике задание значится как «Задание №14»
Приглашаю посмотреть видеоролик по решению задачи категории С2 (в новом формате ЕГЭ по математике – «Задание №16») ЕГЭ по математике . Задача была представлена А. Лариным в одной из тренировочных работ.
Условие: В основании треугольной пирамиды SABC лежит прямоугольный треугольник АВС. Середина D гипотенузы этого треугольника является основанием высоты SD данной пирамиды. Известно, что SD=2, AC=4, BC=3. Через середину высоты SD проведено сечение пирамиды плоскостью, параллельной ребрам AC и SB. Найти площадь этого сечения.
Предлагаю следующую задачу для самостоятельного решения:
На ребре МВ правильной пирамиды МАВС взяты точка К – середина этого ребра и точка L – середина отрезка ВК. Постройте сечение пирамиды плоскостью, проходящей через точку L параллельно прямым КА и МС. Найдите площадь полученного сечения, если сторона основания равна , а боковое ребро равно 2.
Видео:10 класс, 14 урок, Задачи на построение сеченийСкачать

Пособие «Успешное решение стереометрической задачи»
Видео:Сечение Пирамиды Плоскостью Параллельной боковому ребруСкачать

«Календарь счастливой жизни:
инструменты и механизм работы
для достижения своих целей»
Сертификат и скидка на обучение каждому участнику
Муниципальное общеобразовательное учреждение
«Новомичуринская средняя общеобразовательная школа №1»
Пронского района Рязанской области
Пособие по решению
(№14 ЕГЭ по математике)
Козлова Елена Александровна,
МОУ «Новомичуринская средняя
общеобразовательная школа № 1»
Угол между скрещивающимися прямыми …………………………………….
Площади сечений многогранников ……………………………………………
Расстояние от точки до плоскости …………………………………………….
Расстояние от точки до прямой ………………………………………………..
Угол между прямой и плоскостью ……………………………………………..
Расстояние между скрещивающимися прямыми ……………………………..
«Вдохновение есть расположение души к живейшему принятию впечатлений и соображению понятий, следственно и объяснению оных. Вдохновение нужно в геометрии, как и в поэзии».
Задание № 14 (С2) Единого государственного экзамена по математике представляет стереометрическую задачу. При решении такого вида задач используют поэтапно вычислительный или координатно-векторный методы.
В данном пособии даны рекомендации к решению и приведены решения некоторых задач именно поэтапно вычислительным методом (многие решения представлены учениками 10 – 11 классов 2012 – 2015 уч. г.). Этот метод является традиционным и требует от учащихся знание теории, практических умений и навыков, а также развитого пространственного воображения. В пособии много задач для самостоятельного решения, к которым даны ответы. Его можно использовать как на уроках геометрии, так и во внеурочное время для подготовки к ЕГЭ.
Желаю всем, кто увлечён геометрией, с вдохновением решать стереометрические задачи!
Угол между скрещивающимися прямыми
Определение. Две прямые называются скрещивающимися, если они не лежат в одной плоскости.
Признак скрещивающихся прямых. Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые являются скрещивающимися.
Определение. Углом между двумя пересекающимися прямыми называется наименьший из углов, образованных при пересечении прямых.
Величина угла между двумя пересекающимися прямыми принадлежит промежутку (0 0 ; 90 0 ).
Определение. Углом между скрещивающимися прямыми называется угол между пересекающимися прямыми, соответственно параллельными данным скрещивающимся.
При решении задач на данную тему сначала производят параллельный перенос одной из скрещивающихся прямых до пересечения с другой прямой. Затем находят величину угла между двумя пересекающимися прямыми либо из прямоугольного треугольника, либо из произвольного треугольника, используя теорему косинусов по формуле , где a и b – длины сторон треугольника АВС, заключающих искомый угол.
Полезно помнить следующие утверждения:
скрещивающиеся ребра правильной треугольной пирамиды взаимно перпендикулярны;
диагональ основания правильной четырехугольной пирамиды и скрещивающееся с ней боковое ребро взаимно перпендикулярны;
диагональ правильной четырехугольной призмы и скрещивающаяся с ней диагональ основания взаимно перпендикулярны.
Задачи для самостоятельного решения
В кубе АС 1 найдите угол между прямыми А 1 D и D 1 Е, где Е – середина ребра СС 1 .
В кубе АС 1 найдите угол между прямыми А D 1 и DM , где М – середина ребра D 1 C 1 .
В кубе АС 1 точки Р и М – середины ребер А 1 В 1 и В 1 С 1 соответственно. Найдите косинус угла между прямыми АР и ВМ.
На ребре СС 1 куба АС 1 отмечена точка Е так, что СЕ : ЕС 1 = 1 : 2. Найдите угол между прямыми ВЕ и АС 1 .
Сторона основания правильной треугольной призмы АВСА 1 В 1 С 1 равна 8. Высота призмы равна 6. Найдите угол между прямыми СА 1 и АВ 1 .
В правильной треугольной призме АВСА 1 В 1 С 1 все ребра которой равны 1, найдите косинус угла между прямыми АВ и СА 1 .
В правильной треугольной призме АВСА 1 В 1 С 1 все ребра которой равны 1, найдите косинус угла между прямыми АВ 1 и ВС 1 .
В правильной треугольной призме АВСА 1 В 1 С 1 сторона основания равна 4, высота равна 10. Точки К и М – середины ребер АС и А 1 В 1 соответственно. Найдите косинус угла между прямыми АС 1 и КМ.
Боковое ребро правильной треугольной пирамиды SABC равно 6, а косинус угла ASB при вершине боковой грани равен . Точка М – середина ребра SC . Найдите косинус угла между прямыми ВМ и SA .
В правильной четырехугольной пирамиде SABCD сторона основания равна 4. Точка К – середина ребра SB . Тангенс угла между прямыми SD и СК равен 2. Найдите площадь боковой поверхности пирамиды.
Дана правильная четырехугольная пирамида МАВС D . Сторона основания пирамиды равна 5. Тангенс угла между прямыми DM и AL , где L – середина МВ, равен . Найдите высоту данной пирамиды.
В правильном тетраэдре АВС D найдите угол между высотой DH тетраэдра и медианой боковой грани BCD .
Длины всех ребер правильной четырехугольной пирамиды РАВС D равны между собой. Найдите угол между прямыми РН и ВМ, если отрезок РН – высота данной пирамиды, точка М – середина её бокового ребра АР.
Пример 1. В правильной треугольной призме АВСА 1 В 1 С 1 все ребра которой равны 1, найдите косинус угла между прямыми АВ 1 и ВС 1 .
Пример 2. В правильном тетраэдре АВС D найдите угол между высотой DH тетраэдра и медианой боковой грани BCD .
Пример 3. Дана правильная четырехугольная пирамида МАВС D . Сторона основания пирамиды равна 5. Тангенс угла между прямыми DM и AL , где L – середина МВ, равен . Найдите высоту данной пирамиды.
Решение Казаченко Виктории (11 класс, 2013 – 2014 уч. год).
Пример 4. В правильной треугольной призме АВСА 1 В 1 С 1 сторона основания равна 4, высота равна 10. Точки К и М – середины ребер АС и А 1 В 1 соответственно. Найдите косинус угла между прямыми АС 1 и КМ.
Решение Каковкиной Юлии (10 класс, 2014 – 2015 уч. год).
Площади сечений многогранников
Задачи для самостоятельного решения
В прямоугольном параллелепипеде АС 1 известны ребра АВ = 5, А D = 4, АА 1 = 9. Точка О принадлежит ребру ВВ 1 и делит его в отношении 4 : 5, считая от вершины В. Найдите площадь сечения этого параллелепипеда плоскостью, проходящей через точки А, О и С 1 .
На ребре АВ прямоугольного параллелепипеда АС 1 взята точка Е так, что АЕ : ЕВ = 4 : 1. Найдите площадь сечения плоскостью ЕСА 1 , если АВ = 5, А D = 4, АА 1 = 1.
В правильной четырехугольной призме АС 1 сторона основания равна 6, а боковое ребро АА 1 = 1. Точка F принадлежит ребру С 1 D 1 и делит его в отношении 2 : 1, считая от вершины С 1 . Найдите площадь сечения этой призмы плоскостью, проходящей через точки А, С и F .
В правильной четырехугольной призме АС 1 сторона основания равна 11, а боковое ребро АА 1 = 7. Точка К принадлежит ребру В 1 С 1 и делит его в отношении 8 : 3, считая от вершины В 1 . Найдите площадь сечения этой призмы плоскостью, проходящей через точки В, D и К.
Сторона основания правильной треугольной призмы АВСА 1 В 1 С 1 равна 30. На ребрах АС, АВ и А 1 В 1 выбрали точки К, Р и М соответственно так, что АК : КС = АР : РВ = В 1 М : МА 1 = 2 : 1. Площадь сечения призмы плоскостью КРМ равна 210. Найдите площадь боковой грани данной призмы.
В правильной треугольной пирамиде S АВС с основанием АВС проведено сечение через середины ребер АВ и ВС и вершину S . Найдите площадь сечения, если боковое ребро пирамиды равно 10, а сторона основания равна 12.
В правильной треугольной пирамиде МАВС с основанием АВС сторона основания равна 8, а боковое ребро равно 16. На ребре АС находится точка D , на ребре АВ находится точка Е, а на ребре АМ – точка L . Известно, что CD = BE = LM = 4. Найдите площадь сечения пирамиды плоскостью, проходящей через точки E , D , L .
В правильной треугольной пирамиде МАВС с вершиной М высота равна 3, а боковые ребра равны 6. Найдите площадь сечения этой пирамиды плоскостью, проходящей через середины ребер АВ и АС параллельно прямой МА.
МАВС – правильная пирамида, основание АВС – правильный треугольник со стороной 3. Ребро МА перпендикулярно плоскости АВС, ребро МВ = 5. На ребре АС находится точка D , на ребре АМ – точка L , на ребре АВ – точка Е. А D = 2, ВЕ = М L = 1. Найдите площадь сечения пирамиды плоскостью, проходящей через точки Е, D и L .
В правильной треугольной пирамиде SABC с основанием АВС сторона основания равна 8, угол ASB равен 36 0 . На ребре SC взята точка М так, что АМ – биссектриса угла SAC . Найдите площадь сечения пирамиды плоскостью, проходящей через точки А. М, В.
В правильной треугольной пирамиде SABC с вершиной S угол между боковым ребром и плоскостью основания равен 60 0 , сторона основания равна 1, SH – высота пирамиды. Найдите площадь сечения пирамиды плоскостью, проходящей через точку Н параллельно ребрам SA и ВС.
Высота правильной треугольной пирамиды равна стороне ее основания, длина которого равна а . Найдите площадь сечения пирамиды плоскостью, проходящей через сторону основания перпендикулярно противоположному ребру.
В правильной треугольной пирамиде SABC боковое ребро SA = 5, а сторона основания АВ = 4. Найдите площадь сечения пирамиды плоскостью, проходящей через ребро АВ перпендикулярно ребру SC .
В правильной треугольной пирамиде SABC с вершиной S сторона основания равна 4. Через прямую АВ проведено сечение, перпендикулярное ребру SC , площадь которого равна 18. Найдите длину бокового ребра пирамиды.
Через сторону основания правильной треугольной пирамиды проведена плоскость перпендикулярно противоположному ребру. Сторона основания пирамиды равна а , секущая плоскость делит боковое ребро в отношении 3 : 2, считая от вершины пирамиды. Найдите боковое ребро и площадь боковой поверхности пирамиды.
Площадь боковой поверхности правильной четырехугольной пирамиды SAB С D равна 108, а площадь полной поверхности этой пирамиды равна 144. Найдите площадь сечения, проходящего через вершину S этой пирамиды и через диагональ ее основания.
В правильной четырехугольной пирамиде МАВС D боковое ребро равно 8, высота пирамиды равна 2. Найдите площадь сечения, проходящего через прямую BD и середину F ребра МС.
Высота правильной четырехугольной пирамиды равна 80, сторона основания равна 120. Вычислить площадь сечения, проходящего через центр основания параллельно боковой грани.
В правильной четырехугольной пирамиде МАВС D с вершиной М стороны основания равны 3, а боковые ребра равны 8. Найдите площадь сечения пирамиды плоскостью, проходящей через точку В и середину ребра MD параллельно прямой АС.
В правильной пирамиде МАВС D АМ = 4, А D = 3. Постройте сечение пирамиды плоскостью, проходящей через диагональ В D основания параллельно ребру МА и найдите его площадь.
В правильной треугольной призме все ребра равны 1. Точка Е – середина ребра АС. Найдите площадь сечения призмы плоскостью А 1 В 1 Е.
Пример 1. Высота правильной треугольной пирамиды равна стороне ее основания, длина которого равна а . Найти площадь сечения пирамиды плоскостью, проходящей через сторону основания перпендикулярно противоположному ребру.
Пример 2. На ребре АВ прямоугольного параллелепипеда АС 1 взята точка Е так, что АЕ : ЕВ = 4 : 1. Найдите площадь сечения плоскостью ЕСА 1 , если АВ = 5, А D = 4, АА 1 = 1.
Решение Перемыщевой Анны (10 класс, 2014 – 2015 уч. год).
Пример 3. Сторона основания правильной треугольной призмы АВСА 1 В 1 С 1 равна 30. На ребрах АС, АВ и А 1 В 1 выбрали точки К, Р и М соответственно так, что АК : КС = АР : РВ = В 1 М : МА 1 = 2 : 1. Площадь сечения призмы плоскостью КРМ равна 210. Найдите площадь боковой грани данной призмы.
Решение Лутхова Андрея (10 класс, 2014 – 2015 уч. год).
Пример 4. Высота правильной четырехугольной пирамиды равна 80, сторона основания равна 120. Вычислить площадь сечения пирамиды плоскостью, проходящей через центр основания параллельно боковой грани.
Расстояние от точки до плоскости
Определение. Расстоянием от точки А до плоскости , не содержащей эту точку, называется длина перпендикуляра, проведенного из точки А к плоскости .
Признак перпендикулярности прямой и плоскости. Если прямая перпендикулярна к двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна к этой плоскости.
Признак перпендикулярности двух плоскостей. Если одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости, то такие плоскости перпендикулярны.
Признак параллельности прямой и плоскости. Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна данной плоскости.
Признак параллельности двух плоскостей. Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны.
При решении задач по данной теме, применяют метод площадей, подобие треугольников, метод объемов.
Метод площадей. Если площадь треугольника со сторонами a , b и с равна S и к стороне b этого треугольника проведена высота h , то h = .
Можно воспользоваться формулой: h b = .
Метод объемов. Если объем пирамиды АВСМ равен V , то расстояние от точки М до плоскости АВС находят по формуле: . При данном методе нет необходимости в обоснованном построении перпендикуляра из точки к плоскости.
Правила, которые помогут решить некоторые задачи.
Правило 1. Чтобы найти расстояние от данной точки до данной плоскости, достаточно найти расстояние от произвольной точки прямой, содержащей данную точку, до параллельной ей данной плоскости.
Правило 2. Чтобы найти расстояние от данной точки до данной плоскости, достаточно найти расстояние от произвольной точки плоскости, содержащей данную точку, до параллельной ей данной плоскости.
Необходимо знать, что:
в правильной треугольной пирамиде скрещивающиеся ребра взаимно перпендикулярны;
плоскость, проходящая через высоту правильной пирамиды (треугольной, четырехугольной, шестиугольной) и высоту её боковой грани (апофему), перпендикулярна этой боковой грани;
диагональ куба перпендикулярна плоскости, проведенной через концы трех ребер куба, выходящих из той же вершины, что и диагональ.
Задачи для самостоятельного решения
В кубе AC 1 плоскость проходит через прямую А 1 В 1 и середину ребра DD 1 . Найдите расстояние от середины ребра CD до этой плоскости, если ребро куба равно 4.
В кубе AC 1 все ребра равны 1. Найдите расстояние от середины отрезка ВС 1 до плоскости АВ 1 D 1 .
Ребро куба AC 1 равно . Найдите расстояние от вершины С до плоскости BDC 1 .
В единичном кубе AC 1 найдите расстояние от точки А до плоскости BDC 1 .
В основании прямого параллелепипеда АС 1 лежит квадрат ABCD площади 36. Найдите расстояние от точки А 1 до плоскости ВС 1 D , если высота параллелепипеда равна 12.
В правильной треугольной призме ABCA 1 B 1 C 1 все ребра которой равны 1, найдите расстояние от точки А до плоскости СА 1 В 1 .
В правильной шестиугольной призме ABCDEFA 1 B 1 C 1 D 1 E 1 F 1 все ребра равны 1. Найдите расстояния от точки В до плоскостей FB 1 C 1 и DEA 1 .
В правильной треугольной пирамиде SABC с основанием АВС боковое ребро равно 5, а сторона основания равна 6. Найдите расстояние от вершины А до плоскости SBC .
В правильной шестиугольной пирамиде М ABCDEF , стороны основания которой равны 1, а боковые ребра равны 4, найти расстояние
от центра основания пирамиды до грани EMD ;
от середины ребра ВС до плоскости грани ЕМ D .
В правильной четырехугольной пирамиде PABCD c основанием ABCD точка М – середина ребра РА, точка К – середина ребра РВ. Найдите расстояние от вершины А до плоскости СМК, если РС = 6, АВ = 4.
SABCD – правильная четырехугольная пирамида. Боковое ребро SA = , сторона основания равна 2. Найдите расстояние от точки В до плоскости ADM , где М – середина ребра SC .
В правильной четырехугольной пирамиде SABCD с основанием ABCD сторона основания равна 6. Точка К – середина ребра SC . Через прямую АК проведено сечение параллельное одной из диагоналей основания, площадь которого равна 60. Найдите расстояние от точки В до плоскости сечения.
В правильной четырехугольной пирамиде М ABCD АР = 4, А D = 3. Постройте сечение пирамиды плоскостью, проходящей через диагональ В D основания параллельно ребру МА и найдите расстояние от точки М до плоскости сечения.
Ребро SA пирамиды SABC перпендикулярно плоскости основания АВС.
Постройте прямую пересечения плоскости, проходящей через середины ребер АВ, АС, S А, и плоскости, проходящей через середину ребра ВС и перпендикулярной ему.
Найдите расстояние от вершины А до плоскости, проходящей через середины ребер АВ, АС и SA , если SA = , AB = AC = 5, BC = 2.
📹 Видео
Построение сечения пирамиды по трем точкамСкачать

Как строить сечения параллелепипедаСкачать

Построение сечений (часть 1). Пирамиды. сечениеСкачать

Геометрия 10 класс. Подготовка к ЕГЭ. Площадь сечения.Скачать

Как строить сечения тетраэдра и пирамидыСкачать

ПОСТРОЕНИЕ СЕЧЕНИЙ ТЕТРАЭДРА ПЛОСКОСТЬЮСкачать

Построение линии пересечения поверхности пирамиды с проецирующей плоскостьюСкачать

Как строить сеченияСкачать

1.3. Пирамиды. Сечения.Скачать

Видеоразбор задания с2 из егэ 2013 от 3 июняСкачать

№3. Как строить сечения пирамидСкачать

ЕГЭ Задание 14 Правильная пирамида Площадь сеченияСкачать

Стереометрия 10 класс. Часть 1 | МатематикаСкачать

№83. Изобразите параллелепипед ABCDA1B1C1D1 и постройте его сечение плоскостью, проходящей черезСкачать

№14 из профильного ЕГЭ по математике. Как строить сечения на изи. Серия-1Скачать

Построение сечений Занятие 1Скачать
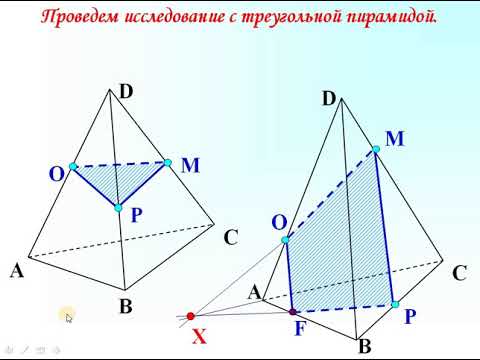
ЕГЭ 3 июня 2013. Площадь сечения четырёхугольной пирамидыСкачать









