Отношение высоты подобных треугольников

Признака подобия треугольников

Две фигуры `F` и `F’` называются подобными, если они переводятся друг в друга преобразованием подобия, т. е. таким преобразованием, при котором расстояния между точками изменяются (увеличиваются или уменьшаются) в одно и то же число раз. Если фигуры `F` и `F’` подобны, то пишется `F

F’`. Напомним, что запись подобия треугольников `Delta ABC

Delta A_1 B_1 C_1` означает, что вершины, совмещаемые преобразованием подобия, стоят на соответствующих местах, т. е. `A` переходит в `A_1`, `B` — в `B_1`, `C` — в `C_1`.

Из свойств преобразования подобия следует, что у подобных фигур соответствующие углы равны, а соответствующие отрезки пропорциональны. В частности, если `Delta ABC

Delta A_1B_1C_1`, то `/_ A = /_ A_1`, `/_ B = /_ B_1`, `/_ C = /_ C_1`,

`A_1B_1 : AB = B_1C_1 : BC = C_1A_1 : CA`.

Два треугольника подобны, если:

1. два угла одного соответственно равны двум углам другого;

2. две стороны одного пропорциональны двум сторонам другого и углы, образованные этими сторонами, равны;

3. три стороны одного треугольника пропорциональны трём сторонам другого.

В решении задач и доказательстве теорем часто используется утверждение, которое, чтобы не повторять каждый раз, докажем сейчас отдельно.

Если две стороны треугольника пересекает прямая, параллельная третьей стороне (рис. 9), то она отсекает треугольник, подобный данному.

Действительно, из параллельности `MN` и `AC` следует, что углы `1` и `2` равны. Треугольники `ABC` и `MBN` имеют два равных угла: общий угол при вершине `B` и равные углы `1` и `2`. По первому признаку эти треугольники подобны.

И сразу применим это утверждение в следующем примере, в котором устанавливается важное свойство трапеции.

Прямая, проходящая через точку пересечения диагоналей трапеции параллельно её основаниям, пересекает боковые стороны трапеции в точках `M` и `N`. Найти длину отрезка `MN`, если основания трапеции равны `a` и `b`.

1. Пусть `O` — точка пересечения диагоналей, `AD = a`, `BC = b`. Прямая `MN` параллельна основанию `AD` (рис. 10а), следовательно, $$ MOparallel AD$$, треугольники `BMO` и `BAD` подобны, поэтому

2. $$ ADparallel BC$$, `Delta AOD

Delta COB` по двум углам (рис. 10б):

`(OD)/(OB) = (AD)/(BC)`, то есть `(OD)/(OB) = a/b`.

3. Учитывая, что `BD = BO + OD` находим отношение

`(BO)/(BD) = (BO)/(BO + OD) = 1/(1 + OD//BO) = b/(a + b)`.

Подставляя это в (1), получаем `MO = (ab)/(a + b)`; аналогично устанавливаем, что `ON = (ab)/(a + b)`, таким образом `MN = (2ab)/(a + b)`.

Точки `M` и `N` лежат на боковых сторонах `AB` и `CD` трапеции `ABCD` и $$ MNparallel AD$$ (рис. 11а). Найти длину `MN`, если `BC = a`, `AD = 5a`, `AM : MB = 1:3`.

1. Пусть $$ BFVert CD$$ и $$ MEVert CD$$ (рис. 11б), тогда `/_ 1 = /_ 2`, `/_ 3 = /_ 4` (как соответствующие углы при пересечении двух параллельных прямых третьей) и `Delta AME

Delta MBF`. Из подобия следует `(AE)/(MF) = (AM)/(MB) = 1/3`.

2. Обозначим `MN = x`. По построению `BCNF` и `MNDE` — параллелограммы, `FN = a`, `ED = x` и, значит, `MF = x — a`; `AE = 5a — x`. Итак, имеем `(5a — x)/(x — a) = 1/3`, откуда находим `x = 4a`.

Напомним, что отношение периметров подобных треугольников равно отношению их сходственных сторон. Верно также следующее утверждение: отношение медиан, биссектрис и высот, проведённых к сходственным сторонам в подобных треугольниках, равно отношению сходственных сторон.

Отношение радиусов вписанных окружностей, как и отношение радиусов описанных окружностей, в подобных треугольниках также равно отношению сходственных сторон.

Попытайтесь доказать это самостоятельно.

Прямоугольные треугольники подобны, если:

1. они имеют по равному острому углу;

2. катеты одного треугольника пропорциональны катетам другого;

3. гипотенуза и катет одного треугольника пропорциональны гипотенузе и катету другого.

Два первых признака следуют из первого и второго признаков подобия треугольников, поскольку прямые углы равны. Третий признак следует, например, из второго признака подобия и теоремы Пифагора.

Заметим, что высота прямоугольного треугольника, опущенная на гипотенузу, разбивает его на два прямоугольных треугольника, подобных между собой и подобных данному. Доказанные в § 1 метрические соотношения Свойств 1, 2, 3 можно доказать, используя подобие указанных треугольников.

СВОЙСТВА ВЫСОТ И БИССЕКТРИС

Если в треугольнике `ABC` нет прямого угла, `A A_1` и `BB_1` — его высоты, то `Delta A_1B_1C

Delta ABC` (этот факт можно сформулировать так: если соединить основания двух высот, то образуется треугольник, подобный данному).

Как всегда, полагаем `AB = c`, `BC = a`, `AC = b`.
а) Треугольник `ABC` остроугольный (рис. 12а).

В треугольнике `A A_1C` угол `A_1` — прямой, `A_1C = AC cos C = ul (b cos C)`.

В треугольнике `B B_1C` угол `B_1` — прямой, `B_1C = BC cos C = ul (a cos C)`.

В треугольниках `A_1 B_1C` и `ABC` угол `C` общий, прилежащие стороны пропорциональны: `(A_1C)/(AC) = (B_1C)/(BC) = cos C`.

Таким образом, `Delta A_1 B_1 C

Delta ABC` с коэффициентом подобия `ul (cos C)`. (Заметим, что `/_ A_1 B_1 C = /_B`).
б) Треугольник `ABC` — тупоугольный (рис. 12б), угол `C` — острый, высота `A A_1` проведена из вершины тупого угла.

$$left.begin
Delta AA_1C, angle A_1 =90^circ Rightarrow A_1C=ACcdot cos C =b cos C;\
Delta BB_1C, angle B_1 =90^circ Rightarrow B_1C=BCcdot cos C =a cos C,
end
right>Rightarrow Delta A_1B_1Csim Delta ABC,$$

коэффициент подобия `ul (cos C)`, `/_ A_1 B_1 C = /_B`.

Случай, когда угол `B` тупой, рассматривается аналогично.
в) Треугольник `ABC` — тупоугольный (рис. 12в), угол `C` — тупой, высоты `A A_1` и `B B_1` проведены из вершин острых углов.

`varphi = /_ BCB_1 = /_ ACA_1 = 180^@ — /_ C`, `cos varphi = — cos C = |cos C|`.

$$left.begin
Delta AA_1C, angle A_1 =90^circ Rightarrow A_1C=ACcdot cosvarphi =b |cos C|;\
Delta BB_1C, angle B_1 =90^circ Rightarrow B_1C=BCcdot cosvarphi =b |cos C|,
end
right>Rightarrow Delta A_1B_1Csim Delta ABC$$

с коэффициентом подобия `ul (k = |cos C|`, `(/_A_1B_1C=/_B)`.

В остроугольном треугольнике `ABC` проведены высоты `A A_1`, `B B_1`, `C C_1` (рис. 13).

Треугольник, вершинами которого служат основания высот, называется «высотным» треугольником (или ортотреугольником).

Доказать, что лучи `A_1 A`, `B_1 B` и `C_1 C` являются биссектрисами углов высотного треугольника `A_1 B_1 C_1` (т. е. высоты остроугольного треугольника являются биссектрисами ортотреугольника).

По первой лемме о высотах `Delta A_1 B_1 C

Delta ABC`, `/_ A_1 B_1 C = /_ B`.

Аналогично `Delta AB_1C_1

Delta ABC`, `/_ AB_1 C_1 = /_ B`, т. е. `/_A_1 B_1C = /_ AB_1 C_1`.

Так как `BB_1` — высота, то `/_AB_1B = /_CB_1B = 90^@`.

Поэтому `/_C_1B_1B = /_A_1B_1B = 90^@ — /_B`, т. е. луч `B_1B` — биссектриса угла `A_1B_1C_1`.

Аналогично доказывается, что `A A_1` — биссектриса угла `B_1 A_1 C_1` и `C_1C` — биссектриса угла `B_1 C_1 A_1`.

Высоты `A A_1`, `B B_1` треугольника `ABC` пересекаются в точке `H` (рис. 14). Доказать, что имеет место равенство `AH * H A_1 = BH * HB_1`, т. е. произведение отрезков одной высоты равно произведению отрезков другой высоты.

Delta BHA_1`, имеют по равному острому углу при вершине `H` (заметим, что этот угол равен углу `C`). Из подобия следует `(AH)/(BH) = (HB_1)/(HA_1)`, откуда `AH * HA_1 = BH * HB_1`. Для тупоугольного треугольника утверждение также верно. Попробуйте доказать самостоятельно.

Высоты `A A_1` и `B B_1` треугольника `ABC` пересекаются в точке `H`, при этом `BH = HB_1` и `AH = 2 HA_1` (рис. 15). Найти величину угла `C`.

1. По условию пересекаются высоты, поэтому треугольник остроугольный. Положим `BH = HB_1 = x` и `HA_1 = y`, тогда `AH = 2y`. По второй лемме о высотах `AH * HA_1 = BH * HB_1`, т. е. `x^2 = 2y^2`, `x = y sqrt 2`.
2. В треугольнике `AHB_1` угол `AHB_1` равен углу `C` (т. к. угол `A_1 AC` равен `90^@ — C`), поэтому `cos C = cos (/_ AHB_1) = x/(2y) = sqrt 2/ 2`. Угол `C` — острый, `/_ C = 45^@`.

Установим ещё одно свойство биссектрисы угла треугольника.

Биссектриса внутреннего угла треугольника делит противолежащую этому углу сторону на отрезки, пропорциональные прилежащим сторонам, т. е. если `AD` — биссектриса треугольника `ABC`, то `(BD)/(DC) = (AB)/(AC)`.

Проведём через точку `B` прямую параллельно биссектрисе `DA`, пусть `K` — её точка пересечения с прямой `AC` (рис. 16).

Параллельные прямые `AD` и `KB` пересечены прямой `KC`, образуются равные углы `1` и `3`. Те же прямые пересечены и прямой `AB`, здесь равные накрест лежащие углы `2` и `4`. Но `AD` — биссектриса, `/_1 = /_2`, следовательно `/_3 = /_4`. Отсюда следует, что треугольник `KAB` равнобедренный, `KA = AB`.
По теореме о пересечении сторон угла параллельными прямыми из $$ ADVert KB$$ следует `(BD)/(DC) = (KA)/(AC)`. Подставляя сюда вместо `KA` равный ему отрезок `AB`, получим `(BD)/(DC) = (AB)/(AC)`. Теорема доказана.

Биссектриса треугольника делит одну из сторон треугольника на отрезки длиной `3` и `5`. Найти в каких пределах может изменяться периметр треугольника.

Пусть `AD` — биссектриса и `BD = 3`, `DC = 5` (рис. 17).

По свойству биссектрисы `AB : AC = 3:5`. Положим `AB = 3x`, тогда `AC = 5x`. Каждая сторона треугольника должна быть меньше суммы двух других сторон, т. е. `ul (5x 1`.

Периметр треугольника `P = 8 + 8x = 8(1 + x)`, поэтому `ul (16

Видео:8 класс, 21 урок, Отношение площадей подобных треугольниковСкачать

Подобные треугольники

Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Определение

Подобные треугольники — треугольники, у которых углы соответственно равны, а стороны одного соответственно пропорциональны сторонам другого треугольника.

Коэффициентом подобия называют число k , равное отношению сходственных сторон подобных треугольников.

Сходственные (или соответственные) стороны подобных треугольников — стороны, лежащие напротив равных углов.

Видео:Подобные треугольникиСкачать

Признаки подобия треугольников

I признак подобия треугольников

Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.

II признак подобия треугольников

Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.

Видео:Как ПОНЯТЬ ГЕОМЕТРИЮ за 5 минут — Подобие ТреугольниковСкачать

Свойства подобных треугольников

• Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
• Отношение периметров подобных треугольников равно коэффициенту подобия.
• Отношение длин соответствующих элементов подобных треугольников (в частности, длин биссектрис, медиан, высот и серединных перпендикуляров) равно коэффициенту подобия.

Видео:№543. Докажите, что отношение сходственных сторон подобных треугольников равноСкачать

Примеры наиболее часто встречающихся подобных треугольников

1. Прямая, параллельная стороне треугольника, отсекает от него треугольник, подобный данному.

2. Треугольники и , образованные отрезками диагоналей и основаниями трапеции, подобны. Коэффициент подобия –

3. В прямоугольном треугольнике высота, проведенная из вершины прямого угла, разбивает его на два треугольника, подобных исходному.

Здесь вы найдете подборку задач по теме «Подобные треугольники» .

Видео:Геометрия 8 класс : Отношение площадей подобных треугольниковСкачать

Тетрадь для правил по геометрии 8 класс

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Развитие управляющих функций мозга ребёнка: полезные советы и упражнения для педагогов

Сертификат и скидка на обучение каждому участнику

Отношением отрезков AB и CD называется отношение их длин.

=;

Теорема о свойстве биссектрисы треугольника: биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам треугольника. (№535)

Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого.

A = A ₁; В= В₁; С= С₁;

Сходственные стороны – стороны, лежащие против равных углов в подобных треугольниках.

Коэффициент подобия – число, равное отношению сходственных сторон подобных треугольников.

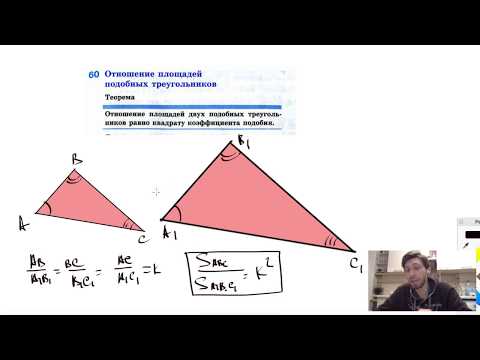
Теорема об отношении площадей подобных треугольников: отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.

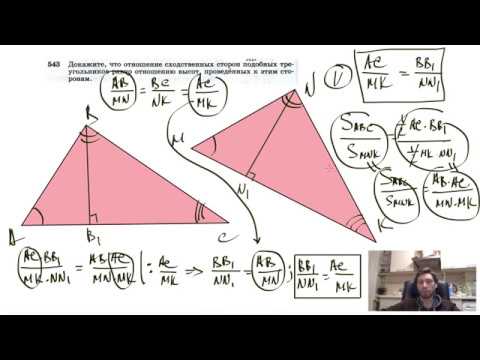
Теорема об отношении высот, проведённых к сходственным сторонам в подобных треугольниках: отношение сходственных сторон подобных треугольников равно отношению высот, проведённым к этим сторонам;

отношение высот, проведённых к сходственным сторонам подобных треугольников, равно коэффициенту подобия. (№543)

;

;

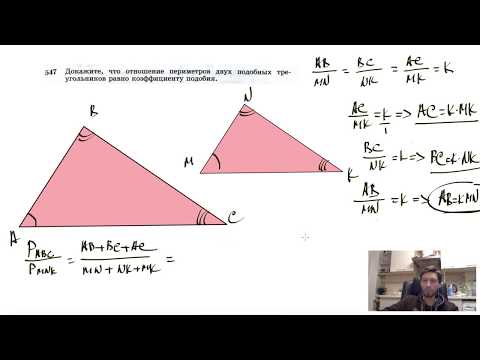
Теорема об отношении периметров двух подобных треугольников: отношение периметров двух подобных треугольников равно коэффициенту подобия. (№547)

ПРИЗНАКИ ПОДОБИЯ ТРЕУГОЛЬНИКОВ

I признак: если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.

A=A ₁ ; В = В ₁ ;

II признак: если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключённые между этими сторонами, равны, то такие треугольники подобны.

; A=A ₁ ;

III признак: если три стороны одного треугольника пропорциональны трём сторонам другого треугольника, то такие треугольники подобны.

;

Теорема о свойстве параллельных прямых, пересекающих стороны угла (более общая формулировка теоремы Фалеса): параллельные прямые, пересекающие стороны угла, отсекают на сторонах угла пропорциональные отрезки. (№556; №558)

=;

=;

Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.

Теорема о средней линии треугольника: средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.

MN – средняя линия треугольника;

Средней линией трапеции называется отрезок, соединяющий середины боковых сторон трапеции.

Теорема о средней линии трапеции: средняя линия трапеции параллельна основаниям и равна их полусумме.

QP – средняя линия трапеции;

Теорема : середины сторон произвольного четырёхугольника являются вершинами параллелограмма. (№567)

Теорема о медианах треугольника : медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2:1, считая от вершины.

Теорема : отрезок, соединяющий середины диагоналей трапеции , параллелен её основаниям и равен полуразности оснований. (№569)

ПРОПОРЦИОНАЛЬНЫЕ ОТРЕЗКИ В ПРЯМОУГОЛЬНОМ ТРЕУГОЛЬНИКЕ

Отрезок XY называется средним пропорциональным (или средним геометрическим) для отрезков AB CD , если XY =;

Теорема : высота прямоугольного треугольника, проведённая из вершины прямого угла, разделяет треугольник на два подобных прямоугольных треугольника, каждый из которых подобен данному треугольнику.

Следствие 1. Высота прямоугольного треугольника, проведённая из вершины прямого угла, есть среднее пропорциональное для отрезков, на которые делится гипотенуза этой высотой.

Следствие 2. Катет прямоугольного треугольника есть среднее пропорциональное для гипотенузы и отрезка гипотенузы, заключённого между катетом и высотой, проведённой из вершины прямого угла.

ADC

ACB

BDC ;

CD = ;

AC = ;

CB= ;

Пропорциональные отрезки в прямоугольном треугольнике

1. ;

2. ;

3. ;

4. ;

5. ;

6. ;

7. ;

СООТНОШЕНИЯ МЕЖДУ СТОРОНАМИ И УГЛАМИ ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА

Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.

Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.

Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.

Тангенс угла равен отношению синуса к косинусу этого угла.

Котангенсом острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему.

Котангенс угла равен отношению косинуса к синусу этого угла.

sin=;

cos=;

tg=;

tg=

ctg=;

ctg=

Основное тригонометрическое тождество

sin 2 +cos 2 =1 ;

Теорема : если острый угол одного прямоугольного треугольника равен острому углу другого прямоугольного треугольника, то синусы этих углов равны, косинусы этих углов равны, тангенсы этих углов равны, котангенсы этих углов равны.

ЗНАЧЕНИЯ sin , cos , tg , ctg ДЛЯ УГЛОВ 30 0 , 45 0 , 60 0

sin

cos

tg

ctg

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 988 человек из 78 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 310 человек из 68 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 673 человека из 75 регионов

Ищем педагогов в команду «Инфоурок»

Видео:Подобие треугольников. Вся тема за 9 минут | ОГЭ по математике | Молодой РепетиторСкачать

Дистанционные курсы для педагогов

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 536 959 материалов в базе

«Актуальность создания школьных служб примирения/медиации в образовательных организациях»

Свидетельство и скидка на обучение каждому участнику

Другие материалы

• 18.01.2016
• 1252
• 0

• 18.01.2016
• 484
• 0

• 18.01.2016
• 682
• 0

• 18.01.2016
• 583
• 0

• 18.01.2016
• 600
• 0

• 18.01.2016
• 6982
• 88

• 18.01.2016
• 476
• 1

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 18.01.2016 2589
• DOCX 208 кбайт
• 6 скачиваний
• Оцените материал:

Настоящий материал опубликован пользователем Коритько Светлана Дмитриевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 6 лет и 1 месяц
• Подписчики: 0
• Всего просмотров: 18547
• Всего материалов: 16

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:Решение задач на тему "Подобные треугольники". 8 классСкачать

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В Томске из-за COVID-19 перенесут каникулы для первоклассников

Время чтения: 1 минута

Полный перевод школ на дистанционное обучение не планируется

Время чтения: 1 минута

Володин призвал выработать единые нормы организации групп продленного дня

Время чтения: 2 минуты

В Томске студентов вузов перевели на дистанционное обучение до конца февраля

Время чтения: 1 минута

В Госдуме предложили доплачивать учителям за работу в классах, где выявлен ковид

Время чтения: 1 минута

Путин поручил обучать педагогов работе с девиантным поведением

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

🌟 Видео

Подобие треугольников (ч.2) | Математика | TutorOnlineСкачать

8 класс, 20 урок, Определение подобных треугольниковСкачать

Геометрия 8 класс (Урок№14 - Определение подобных треугольников. Отношение площадей подобных фигур.)Скачать

Нахождение высоты подобного треугольникаСкачать

60. Отношение площадей подобных треугольниковСкачать

Математика | Соотношения между сторонами и углами в прямоугольном треугольнике.Скачать

ПОДОБНЫЕ ТРЕУГОЛЬНИКИ 8 класс ЗАДАЧИ коэффициент подобияСкачать

Отношение площадей подобных треугольников.Скачать

Подобные треугольникиСкачать

Замечательные точки треугольника | Ботай со мной #030 | Борис Трушин ||Скачать

Задача на подобие треугольников. А ты сможешь решить? | TutorOnline | МатематикаСкачать

№547. Докажите, что отношение периметров двух подобных треугольников равно коэффициенту подобия.Скачать