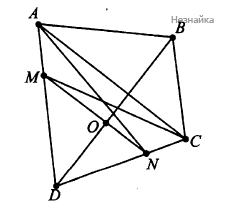
На сторонах ab и cd выпуклого четырехугольника abcd отмечены точки m и n соответственно так (8 видео)

На сторонах ab и cd выпуклого четырехугольника abcd отмечены точки m и n соответственно так

В выпуклом четырёхугольнике ABCD на сторонах AD и CD взяты точки М и N, такие, что каждая из прямых СМ и AN делит ABCD на две фигуры равных площадей.

а) Докажите, что АС параллельно MN.

б) Найдите отношение площадей четырёхугольников ABCD и АВСО, где О — точка пересечения BD и MN.

Из условия следует, что [math]S_=S_=frac12S_[/math] (см. рисунок)

Но тогда для треугольников [math]AND[/math] и [math]MCD[/math] с общим углом [math]D[/math] имеем [math]frac12ADtimes NDtimessinangle D=frac12MDtimes CDtimessinangle D[/math] или [math]frac=frac[/math] . Следовательно, треугольники [math]MND[/math] и [math]ACD[/math] подобны по второму признаку подобия, из чего следует, что [math]ACparallel MN[/math].

б) Так как [math]ACparallel MN[/math], то точки [math]O[/math] и [math]N[/math] равноудалены от прямой [math]AC[/math], а значит, высоты треугольников [math]AOC[/math] и [math]ANC[/math] равны, поэтому их площади также равны. Следовательно, [math]S_=S_+S_=S_[/math], но [math]S_[/math] по площади составляет половину от [math]S_[/math], поэтому и [math]S_[/math] составляет половину от [math]S_[/math] по площади.

Содержание

На сторонах AB, BC, CD и DA четырехугольника ABCD отмечены соответственные точки M N P и Q так что, AM = СP, BN = DQ, BM = DP, NC = QA?
В параллелограмме ABCD на сторонах AB, BC, CD, DA отмечены точки E, F, P, Q, причем AE / AB = BF / BC = СР / CD = DQ / DA = 1 / 3?
В паралелограмме ABCD точки E — середина сторон BC и AD соответсвенно?
ДАЮ 60 БАЛЛОВ?
Сторона bc параллелограмма abcd вдвое больше стороны ab?
На сторонах AB, BC, CD, DA четырёхугольника ABCD отмечены соответственно точки M, N, P, Q так, что AM = CP, BN = DQ, BM = DP, NC = QA?
Сторона ab параллелограмма abcd вдвое больше стороны bc точка N середина стороны ab докажите что cn биссектриса угла bcd?
На стороне BC параллелограмма ABCD взята точка M так, что AB = BM?
На стороне bc выпуклого четырехугольника abcd отмечена точка p, а вне четырёхугольника — точка Q?
В параллелограмме ABCD точки E и К середины сторон BC и AD соответственно?
В четырехугольнике ABCD точки M, N, P, Q соответственно середины сторон AB, BC, CD, DA, докажите, что отрезки MP и NQ точкой пересечения делятся пополам?
На сторонах ab и cd выпуклого четырехугольника abcd отмечены точки m и n соответственно так
Источник задания: Решение 2951. ЕГЭ 2016 Математика, И.В. Ященко. 30 вариантов. Ответ.
🌟 Видео

Видео:Геометрия Стороны AB и CD выпуклого четырехугольника ABCD равны. Через середины диагоналей AC и BDСкачать

На сторонах AB, BC, CD и DA четырехугольника ABCD отмечены соответственные точки M N P и Q так что, AM = СP, BN = DQ, BM = DP, NC = QA?

Геометрия | 5 — 9 классы

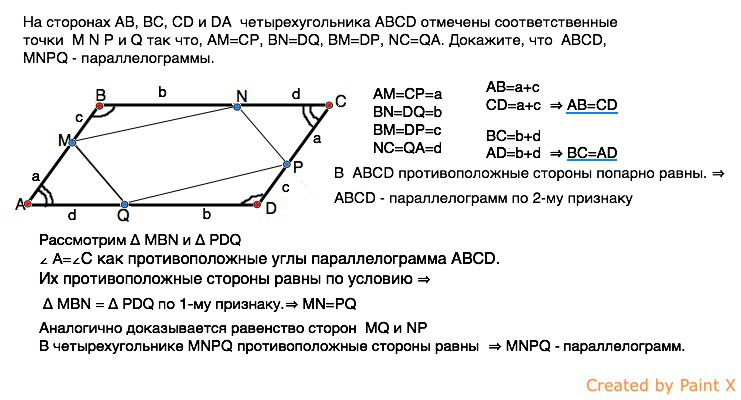
На сторонах AB, BC, CD и DA четырехугольника ABCD отмечены соответственные точки M N P и Q так что, AM = СP, BN = DQ, BM = DP, NC = QA.

Докажите, что ABCD, MNPQ — параллелограммы.

На сторонах AB, BC, CD и DA четырехугольника ABCD отмечены соответственные точки M N P и Q так что, AM = СP, BN = DQ, BM = DP, NC = QA.

Докажите, чтоABCD, MNPQ — параллелограммы.

Обозначим равные отрезки одинаковыми буквами :

СD = a + c ⇒ AB = CD

AD = b + d ⇒ BC = AD

В четырехугольнике АВСD противоположные стороны попарно равны.

АВСD — параллелограмм ( 2 — й признак)

Рассмотрим ∆ MBN и ∆ PDQ

∠А = ∠С как противоположные углы параллелограмма АВСD.

Содержащие эти углы стороны равны по условию⇒

∆ MBN = ∆ PDQ по 1 — му признаку.

Аналогично доказывается равенство сторон MQ и NP

В четырехугольнике MNРQ противоположные стороны равны⇒MNРQ — параллелограмм.

Видео:Геометрия На сторонах AB и BC треугольника ABC отмечены соответственно точки M и K так, что AM = 3BMСкачать

В параллелограмме ABCD на сторонах AB, BC, CD, DA отмечены точки E, F, P, Q, причем AE / AB = BF / BC = СР / CD = DQ / DA = 1 / 3?

В параллелограмме ABCD на сторонах AB, BC, CD, DA отмечены точки E, F, P, Q, причем AE / AB = BF / BC = СР / CD = DQ / DA = 1 / 3.

Докажите, что EFQP — параллелограмм.

Видео:№380. На сторонах АВ, ВС, CD и DA четырехугольника ABCD отмечены соответственно точки М, N, Р и QСкачать

В паралелограмме ABCD точки E — середина сторон BC и AD соответсвенно?

В паралелограмме ABCD точки E — середина сторон BC и AD соответсвенно.

Докажите что четырехугольник AECK — ПАРАЛЛЕЛОГРАММ.

Видео:В треугольнике ABC на сторонах АВ и ВС отмечены точки М и К соответственно, ВМ/АВ = 1/2, ВК/ВС = 4/5Скачать

ДАЮ 60 БАЛЛОВ?

Через точку пересечения диагоналей параллелограмма ABCD проведены две прямые.

Одна из них пересекает стороны AB и CD, соответственно, в точках М и К, вторая — стороны BC и AD, соответственно, в точках N и L.

Докажите, что четырехугольник MNKL — параллелограмм.

Видео:№28. На сторонах АВ и АС треугольника ABC взяты соответственноСкачать

Сторона bc параллелограмма abcd вдвое больше стороны ab?

Сторона bc параллелограмма abcd вдвое больше стороны ab.

Точка E — середина стороны BC.

Докажите, что AE — биссектриса угла BAD.

Видео:ОГЭ 2023 Ященко 12 вариант ФИПИ школе полный разбор!Скачать

На сторонах AB, BC, CD, DA четырёхугольника ABCD отмечены соответственно точки M, N, P, Q так, что AM = CP, BN = DQ, BM = DP, NC = QA?

На сторонах AB, BC, CD, DA четырёхугольника ABCD отмечены соответственно точки M, N, P, Q так, что AM = CP, BN = DQ, BM = DP, NC = QA.

Докажите, что ABCD и MNPQ — — — ПАРАЛЛЕЛОГРАММЫ.

Видео:Геометрия На сторонах AD и BC параллелограмма ABCD взяты соответственно точки M и N, причём MСкачать

Сторона ab параллелограмма abcd вдвое больше стороны bc точка N середина стороны ab докажите что cn биссектриса угла bcd?

Сторона ab параллелограмма abcd вдвое больше стороны bc точка N середина стороны ab докажите что cn биссектриса угла bcd.

Видео:Геометрия Диагонали выпуклого четырехугольника ABCD перпендикулярны. Через середины сторон AB и ADСкачать

На стороне BC параллелограмма ABCD взята точка M так, что AB = BM?

На стороне BC параллелограмма ABCD взята точка M так, что AB = BM.

Докажите, что AM — биссектриса угла BAD.

Видео:Вариант ФИПИ на 100 баллов #10 (математика ЕГЭ профиль)Скачать

На стороне bc выпуклого четырехугольника abcd отмечена точка p, а вне четырёхугольника — точка Q?

На стороне bc выпуклого четырехугольника abcd отмечена точка p, а вне четырёхугольника — точка Q.

При этом отрезки BP и AQ, а также CP и DQ имеют общие середины.

Докажите что отрезки AC и BD имеют общую середину.

Видео:№785. Точки М и N — середины диагоналей АС и BD четырехугольника ABCD.Скачать

В параллелограмме ABCD точки E и К середины сторон BC и AD соответственно?

В параллелограмме ABCD точки E и К середины сторон BC и AD соответственно.

Докажите, что четырехугольник ABEK параллелограмм.

Видео:🔴 ВСЕ ЗАДАНИЯ 26 ИЗ ОТКРЫТОГО БАНКА (ПЕРВАЯ ПОЛОВИНА ВСЕХ ЗАДАЧ) | ОГЭ 2017Скачать

В четырехугольнике ABCD точки M, N, P, Q соответственно середины сторон AB, BC, CD, DA, докажите, что отрезки MP и NQ точкой пересечения делятся пополам?

В четырехугольнике ABCD точки M, N, P, Q соответственно середины сторон AB, BC, CD, DA, докажите, что отрезки MP и NQ точкой пересечения делятся пополам.

На этой странице находится вопрос На сторонах AB, BC, CD и DA четырехугольника ABCD отмечены соответственные точки M N P и Q так что, AM = СP, BN = DQ, BM = DP, NC = QA?. Здесь же – ответы на него, и похожие вопросы в категории Геометрия, которые можно найти с помощью простой в использовании поисковой системы. Уровень сложности вопроса соответствует уровню подготовки учащихся 5 — 9 классов. В комментариях, оставленных ниже, ознакомьтесь с вариантами ответов посетителей страницы. С ними можно обсудить тему вопроса в режиме on-line. Если ни один из предложенных ответов не устраивает, сформулируйте новый вопрос в поисковой строке, расположенной вверху, и нажмите кнопку.

Умножаешь радиус на 2 , получившееся есть сторона квадрата , по формуле https : / / m. Fxyz. Ru / 2 / 70 / 88 / 98 / 94 / находишь радиус описанной окружности ( где a — сторона квадрата).

Вроде так, размеры подпиши.

Если на рисунке дана диметрическая проекция, то вид спереди — это изображение свертикальной стенкой справа.

Пусть О — центр грани EFGH. Точка О принадлежит обоим плоскостям. F1O перпендикулярна eg. F1Of искомый угол а tg a = f1f / fO = 1 / (√2 / 2) = √2.

Найди все точки в системе координат. Потом соедини их линиями, что получишь, то и будет. Квадрат, значит квадрат, если все отрезки линий равны.

У равнобедренной трапеции углы при основаниях равны. Сумма двух углов прилежащих к боковой стороне = 180° 180° — 99° = 81° Ответ : меньший угол = 81°.

Т. к AM = CM То AMB равнобедренный значит углы при основании равны ACM = 50гр. AMC = 180 — 100 = 80гр. BMC = 90 — 50 = 40гр.

40°. Так он опирается на те же точки круга, что и угол, который равен 40°. Эти углы равны.

4 + 7 + 5 = 16 — общее количество частей 32 : 16 = 2см — 1 часть 1)4 * 2 = 8см — первая часть 2)7 * 2 = 14см вторая часть 3)5 * 2 = 10см третья часть Проверка : 8 + 14 + 10 = 32см.

Три прямые, пересекающиеся попарно, образуют три точки пересечения. А) Через три точки, не лежащие на одной прямой, можно провести плоскость, притом только одну. Следовательно, любая прямая, пересекающая прямые a и b, но непроходящие через точку С.

Видео:№369. Найдите углы A, B и C выпуклого четырехугольника ABCD, еслиСкачать

На сторонах ab и cd выпуклого четырехугольника abcd отмечены точки m и n соответственно так

Видео:Геометрия Точки M, K, N, P являются соответственно серединами сторон AB, BC, CD и AD квадрата ABCDСкачать

Источник задания: Решение 2951. ЕГЭ 2016 Математика, И.В. Ященко. 30 вариантов. Ответ.

Задание 16. На сторонах АВ, ВС, CD и AD параллелограмма ABCD отмечены точки K, L, М и N соответственно, причем AK/KB=BL/LC=CM/MD=DN/NA.

а) Докажите, что четырёхугольник KLMN — параллелограмм, а его центр совпадает с центром параллелограмма ABCD.

б) Найдите отношение площадей параллелограммов KLMN и ABCD, если известно, что AK/KB = 2.

а) Так как ABCD – параллелограмм, то , , AB=CD, BC=AD, , . Обозначим через отрезок KB, соответственно, длина отрезка , где — некоторое положительное число. Аналогично определим и для других отрезков (см. рисунок):

Рассмотрим треугольники KBL и MDN, которые равны по двум сторонам и углу (см. рисунок), следовательно, KL=MN. По аналогии из треугольников AKN и CML следует равенство KN=LM. Таким образом, доказали, что KLMN – параллелограмм.

б) Так как , то число . Площадь параллелограмма ABCD можно найти по формуле

Площадь параллелограмма KLMN можно найти как разность между площадью параллелограмма ABCD и четырех равных площадей треугольников KBL, LCM, NDM и ANK: