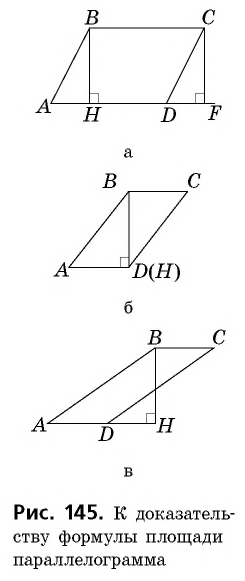
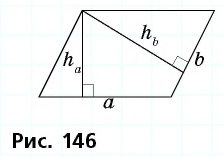
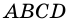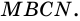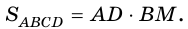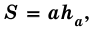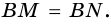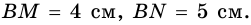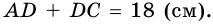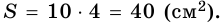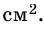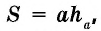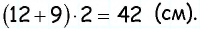Теорема (о площади параллелограмма). Площадь параллелограмма равна произведению его стороны на высоту, проведенную к этой стороне.
Доказательство:
Пусть
1) Проведем высоту 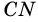
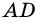
2) 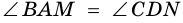
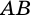
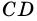
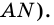
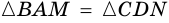
3) Параллелограмм 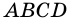
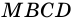
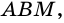
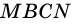
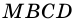
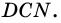
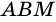
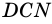
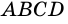
4) 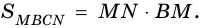
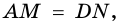
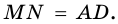
Заметим, что если основание высоты 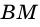
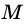
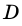
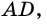
В общем виде формулу площади 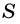
где 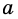
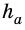
Пример:
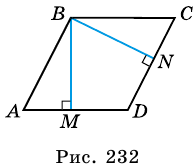
Докажите, что высоты ромба, проведенные из одной вершины, равны.
Доказательство:
Пусть 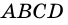
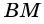
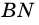
Ромб является параллелограммом, поэтому 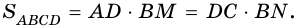
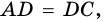
Пример:
Периметр параллелограмма равен 36 см, а его высоты — 4 см и 5 см. Найдите площадь параллелограмма.
Решение:
1) Пусть 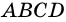
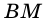
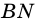
2) 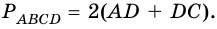
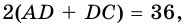
3) Пусть 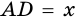
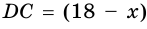
4) Так как по формуле площади параллелограмма 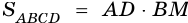
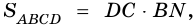
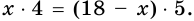
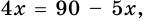
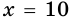
5) Тогда
Ответ. 40
- Площадь параллелограмма
- § 2. Площади параллелограмма, треугольника и трапеции
- Площадь параллелограмма
- Площадь треугольника
- Площадь трапеции
- Задачи
- Ответы к задачам
- Как найти площадь параллелограмма, треугольника, трапеции
- Площадь параллелограмма
- Площадь треугольника
- Готовые работы на аналогичную тему
- Площадь трапеции
- Пример задачи
- 🎥 Видео
Видео:8 класс, 13 урок, Площадь параллелограммаСкачать

Площадь параллелограмма
С помощью формулы площади прямоугольника можно доказать формулу площади произвольного параллелограмма.
Теорема (формула площади параллелограмма)
Площадь параллелограмма равна произведению его стороны на высоту, проведенную к этой стороне:
где 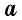
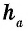
Пусть 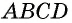
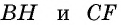
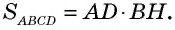
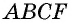
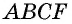
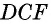
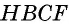
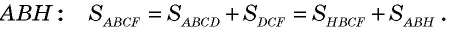
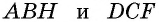
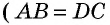
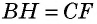
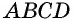
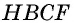
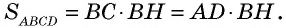
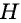
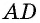
Пример:
Площадь параллелограмма равна 
Решение:
Пусть дан параллелограмм с площадью 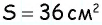
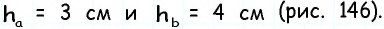
Поскольку
Следовательно, периметр параллелограмма равен
Ответ: 42 см.
Решая приведенную задачу, можно заметить интересную закономерность: чем больше сторона параллелограмма, тем меньше проведенная к ней высота.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Прямоугольник и его свойства
- Ромб и его свойства, определение и примеры
- Квадрат и его свойства
- Трапеция и ее свойства
- Свойство катета прямоугольного треугольника, лежащего против угла в 30°
- Четырехугольник и его элементы
- Четырехугольники и окружность
- Параллелограмм, его свойства и признаки
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Все про ПАРАЛЛЕЛОГРАММ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // ГеометрияСкачать

§ 2. Площади параллелограмма, треугольника и трапеции
Площадь параллелограмма
Условимся одну из сторон параллелограмма называть основанием, а перпендикуляр, проведённый из любой точки противоположной стороны к прямой, содержащей основание, — высотой параллелограмма.
| Площадь параллелограмма равна произведению его основания на высоту. |
Рассмотрим параллелограмм ABCD с площадью S. Примем сторону AD за основание и проведём высоты ВН и СК (рис. 182). Докажем, что S = AD • ВН.
Докажем сначала, что площадь прямоугольника НВСК также равна S. Трапеция АВСК составлена из параллелограмма ABCD и треугольника DCK. С другой стороны, она составлена из прямоугольника НВСК и треугольника АВН. Но прямоугольные треугольники DCK и АВН равны по гипотенузе и острому углу (их гипотенузы АВ и CD равны как противоположные стороны параллелограмма, а углы 1 и 2 равны как соответственные углы при пересечении параллельных прямых АВ и CD секущей AD), поэтому их площади равны.
Следовательно, площади параллелограмма ABCD и прямоугольника НВСК также равны, т. е. площадь прямоугольника НВСК равна S. По теореме о площади прямоугольника S = ВС • ВН, а так как ВС = AD, то S = AD • ВН. Теорема доказана.
Площадь треугольника
Одну из сторон треугольника часто называют его основанием. Если основание выбрано, то под словом «высота» подразумевают высоту треугольника, проведённую к основанию. Теорема
| Площадь треугольника равна половине произведения его основания на высоту. |
Пусть S — площадь треугольника АВС (рис. 183). Примем сторону АВ за основание треугольника и проведём высоту СН. Докажем, что 
Достроим треугольник АВС до параллелограмма ABDC так, как показано на рисунке 183. Треугольники АВС и DCB равны по трём сторонам (ВС — их общая сторона, АВ = CD и АС = BD как противоположные стороны параллелограмма ABDC), поэтому их площади равны. Следовательно, площадь S треугольника АВС равна половине площади параллелограмма ABDC, т. е. 
| Площадь прямоугольного треугольника равна половине произведения его катетов. |
| Если высоты двух треугольников равны, то и площади относятся как основания. |
Воспользуемся следствием 2 для доказательства теоремы об отношении площадей треугольников, имеющих по равному углу.
| Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы. |
Пусть S и S1 — площади треугольников АВС и A1B1C1, у которых ∠A = ∠A1 (рис. 184, а). Докажем, что 
Наложим треугольник A1B1C1 на треугольник ABC так, чтобы вершина А1 совместилась с вершиной А, а стороны А1В1 и A1С1 наложились соответственно на лучи АВ и АС (рис. 184, б). Треугольники АВС и АВ1С имеют общую высоту — CН, поэтому 
Треугольники АВ1С и АВ1С1 также имеют общую высоту — В1Н1, поэтому 
Видео:Площадь параллелограмма треугольника и трапецииСкачать

Площадь трапеции
Для вычисления площади произвольного многоугольника обычно поступают так: разбивают многоугольник на треугольники и находят площадь каждого треугольника. Сумма площадей этих треугольников равна площади данного многоугольника (рис. 185, а). Используя этот приём, выведем формулу для вычисления площади трапеции. Условимся называть высотой трапеции перпендикуляр, проведённый из любой точки одного из оснований к прямой, содержащей другое основание. На рисунке 185, б отрезок ВН (а также отрезок DH1) — высота трапеции ABCD.
| Площадь трапеции равна произведению полусуммы её оснований на высоту. |
Рассмотрим трапецию ABCD с основаниями AD и ВС, высотой ВН и площадью S (см. рис. 185, б).
Диагональ BD разделяет трапецию на два треугольника ABD и BCD, поэтому S = SABD + SBCD.
Примем отрезки AD и ВН за основание и высоту треугольника ABD, а отрезки ВС и DH1 за основание и высоту треугольника BCD. Тогда

Задачи
459. Пусть а — основание, h — высота, a S — площадь параллелограмма. Найдите: a) S, если а = 15 см, h = 12 см; б) а, если S = 34 cм 2 , h = 8,5 см; в) а, если S = 162 cм 2 , h = 1/2a; г) h, если h = 3а, S = 27.
460. Диагональ параллелограмма, равная 13 см, перпендикулярна к стороне параллелограмма, равной 12 см. Найдите площадь параллелограмма.
461. Смежные стороны параллелограмма равны 12 см и 14 см, а его острый угол равен 30°. Найдите площадь параллелограмма.
462. Сторона ромба равна 6 см, а один из углов равен 150°. Найдите площадь ромба.
463. Сторона параллелограмма равна 8,1 см, а диагональ, равная 14 см, образует с ней угол в 30°. Найдите площадь параллелограмма.
464. Пусть а и b — смежные стороны параллелограмма, S — площадь, a h1 и h2 — его высоты. Найдите: a) h2, если а = 18 см, b = 30 см, h1 = 6 см, h2 > h1; б) h1, если а =10 см, 6 =15 см, h2 = 6 см, h2 > h1 в) h1 и h2, если S = 54 см 2 , а = 4,5 см, b = 6 см.
465. Острый угол параллелограмма равен 30°, а высоты, проведённые из вершины тупого угла, равны 2 см и 3 см. Найдите площадь параллелограмма.
466. Диагональ параллелограмма равна его стороне. Найдите площадь параллелограмма, если большая его сторона равна 15,2 см, а один из его углов 45°.
467. Квадрат и ромб, не являющийся квадратом, имеют одинаковые периметры. Сравните площади этих фигур.
468. Пусть а — основание, h — высота, a S — площадь треугольника. Найдите: a) S, если а = 7 см, h = 11 см; б) S, если а = 2√3 см, h = 5 см; в) h, если S = 37,8 см 2 , а — 14 см; г) а, если S = 12 см 2 , h = 3√2 см.
469. Стороны АВ и ВС треугольника АВС равны соответственно 16 см и 22 см, а высота, проведённая к стороне АВ, равна 11 см. Найдите высоту, проведённую к стороне ВС.
470. Две стороны треугольника равны 7,5 см и 3,2 см. Высота, проведённая к большей стороне, равна 2,4 см. Найдите высоту, проведённую к меньшей из данных сторон.
471. Д Найдите площадь прямоугольного треугольника, если его катеты равны: а) 4 см и 11 см; б) 1,2 дм и 3 дм.
472. Площадь прямоугольного треугольника равна 168 см 2 . Найдите его катеты, если отношение их длин равно 7/12.
473. Через вершину С треугольника АВС проведена прямая m, параллельная стороне АВ. Докажите, что все треугольники с вершинами на прямой m и основанием АВ имеют равные площади.
474. Сравните площади двух треугольников, на которые разделяется данный треугольник его медианой.
475. Начертите треугольник АВС. Через вершину А проведите две прямые так, чтобы они разделили этот треугольник на три треугольника, имеющие равные площади.
476. Докажите, что площадь ромба равна половине произведения его диагоналей. Вычислите площадь ромба, если его диагонали равны: а) 3,2 дм и 14 см; б) 4,6 дм и 2 дм.
477. Найдите диагонали ромба, если одна из них в 1,5 раза больше другой, а площадь ромба равна 27 см 2 .
478. В выпуклом четырёхугольнике диагонали взаимно перпендикулярны. Докажите, что площадь четырёхугольника равна половине произведения его диагоналей.
479. Точки D и Е лежат на сторонах АВ и АС треугольника АВС. Найдите: a) SADE, если АВ = 5 см, АС = 6 см, AD = Зсм, АЕ = 2 см, SABC = 10 cм 2 ; б) AD, если АВ = 8 см, АС = 3 см, АЕ = 2 см, SABC = 10 см 2 , SADE = 2 см 2 .
480. Найдите площадь трапеции ABCD с основаниями АВ и CD, если:
а) АВ = 21 см, CD= 17 см, высота ВН равна 7 см;
б) ∠D = 30°, АВ = 2 см, CD = 10 см, DA = 8 см;
в) ВС ⊥ АВ, АВ = 5 см, ВС = 8 см, CD = 13 см.
481. Найдите площадь прямоугольной трапеции, у которой две меньшие стороны равны 6 см, а больший угол равен 135°.
482. Тупой угол равнобедренной трапеции равен 135°, а высота, проведённая из вершины этого угла, делит большее основание на отрезки 1,4 см и 3,4 см. Найдите площадь трапеции.
Ответы к задачам
459. а) 180 см 2 ; б) 4 см; в) 18 см; г) 9.
464. а) 10 см; б) 4 см; в) 12 см и 9 см.
467. Площадь квадрата больше.
468. а) 38,5 см 2 ; б) 5√3 см 2 ; в) г) 4√2 см.
471. а) 22 см 2 ; б) 1,8 дм 2 .
472. 14 см и 24 см.
473. Указание. Воспользоваться теоремой п. 38.
474. Площади треугольников равны.
475. Указание. Сначала разделить сторону ВС на три равные части.
476. а) 224 см 2 ; б) 4,6 дм 2 . Указание. Учесть, что диагонали ромба взаимно перпендикулярны.
477. 6 см и 9 см.
479. а) 2 см 2 ; б) 2,4 см. Указание. Воспользоваться второй теоремой п. 53.
480. а) 133 см 2 ; б) 24 см 2 ; в) 72 см 2 .
Видео:Геометрия 8 класс (Урок№9 - Площадь параллелограмма.)Скачать

Как найти площадь параллелограмма, треугольника, трапеции
Вы будете перенаправлены на Автор24
Видео:Геометрия 8 класс. Площадь параллелограммаСкачать

Площадь параллелограмма
Площадь параллелограмма определяется как произведение длины его стороны, на высоту, проведенную к ней.
Математически это можно записать следующим образом
где $a$ сторона параллелограмма, $h$ — высота, проведенная к этой стороне.
Доказательство.
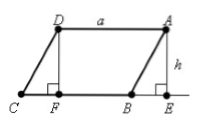
Пусть нам дан параллелограмм $ABCD$, у которого $AD=BC=a$. Проведем высоты $DF$ и $AE$ (рис. 1).
Очевидно, что фигура $FDAE$ — прямоугольник.
[angle BAE=^0-angle A, ] [angle CDF=angle D-^0=^0-angle A-^0=^0-angle A=angle BAE]
Следовательно, так как $CD=AB, DF=AE=h$, по $I$ признаку равенства треугольников $triangle BAE=triangle CDF$. Тогда
Значит по теореме о площади прямоугольника:
Теорема доказана.
Площадь параллелограмма определяется как произведение длины его смежных сторон, на синус угла между этими сторонами.
Математически это можно записать следующим образом
где $a, b$ стороны параллелограмма, $alpha $ — угол между ними.
Доказательство.
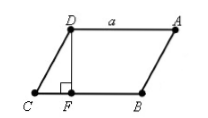
Пусть нам дан параллелограмм $ABCD$, у которого $BC=a, CD=b, angle C=alpha $. Проведем высоту $DF=h$ (рис. 2).
По определению синуса, получим
Значит, по теореме $1$:
Теорема доказана.
Видео:Площадь параллелограмма (доказательство) - 8 класс геометрияСкачать

Площадь треугольника
Площадь треугольника определяется как половина произведения длины его стороны, на высоту, проведенную к ней.
Математически это можно записать следующим образом
где $a$ сторона треугольника, $h$ — высота, проведенная к этой стороне.
Доказательство.
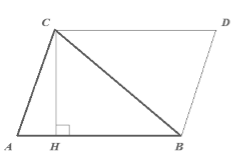
Пусть нам дан треугольник $ABC$, у которого $AB=a$. Проведем высоту $CH=h$. Достроим его до параллелограмма $ABCD$ (рис. 3).
Очевидно, что по $I$ признаку равенства треугольников $triangle ACB=triangle CDB$. Тогда
Значит по теореме $1$:
Теорема доказана.
Готовые работы на аналогичную тему
Площадь треугольника определяется как половина произведения длины его смежных сторон, на синус угла между этими сторонами.
Математически это можно записать следующим образом
где $a, b$ стороны треугольника, $alpha $ — угол между ними.
Доказательство.
Пусть нам дан треугольник $ABC$, у которого $AB=a$. Проведем высоту $CH=h$. Достроим его до параллелограмма $ABCD$ (рис. 3).
Очевидно, что по $I$ признаку равенства треугольников $triangle ACB=triangle CDB$. Тогда
Значит по теореме $1$:
Теорема доказана.
Видео:Площадь параллелограмма, треугольника, трапецииСкачать

Площадь трапеции
Площадь трапеции определяется как половина произведения суммы длин его оснований, на его высоту.
Математически это можно записать следующим образом
Доказательство.
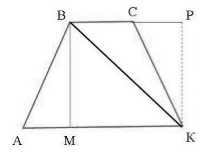
Пусть нам дана трапеция $ABCK$, где $AK=a, BC=b$. Проведем в ней высоты $BM=h$ и $KP=h$, а также диагональ $BK$ (рис. 4).
По теореме $3$, получим
Теорема доказана.
Видео:9 класс, 12 урок, Теорема о площади треугольникаСкачать

Пример задачи
Найти площадь равностороннего треугольника, если длина его стороны равняется $a.$
Решение.
Так как треугольник равносторонний, то все его углы равняются $^0$.
Тогда, по теореме $4$, имеем
Заметим, что результат этой задачи можно применять при нахождении площади любого равностороннего треугольника с данной стороной.
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 19 05 2021
🎥 Видео
Геометрия 9 класс (Урок№14 - Теорема о площади треугольника.)Скачать

8 класс, 14 урок, Площадь треугольникаСкачать

Доказательство теоремы о площади параллелограммаСкачать

Теорема о площади параллелограмма. Доказательство. Геометрия 9 классСкачать

Геометрия 8 класс (Урок№10 - Площадь треугольника.)Скачать

Как находить площадь любой фигуры? Геометрия | МатематикаСкачать

Все формулы площади параллелограмма 🔥 #умскул_профильнаяматематика #никитасалливан #егэпрофильСкачать

Площадь параллелограммаСкачать

Теорема о площади параллелограмма. 8 классСкачать

Вывод формулы площади параллелограмма и треугольникаСкачать

Почему площадь параллелограмма равна произведению его основания на высотуСкачать