Этот онлайн калькулятор находит центроид, или барицентр (центр тяжести) треугольника по координатам его вершин
Центр тяжести (центр масс, барицентр) треугольника для треугольника с равномерно распределённой массой (или в вершинах которого находятся равные массы) находится в центроиде треугольника. Центроидом называется точка пересечения медиан треугольника. Центроид относится к так называемым замечательным точкам треугольника. Например, помимо того, что он является центром тяжести, он также делит каждую медиану в отношении 2:1, считая от вершины, а три отрезка прямых, соединяющих вершины треугольника с центроидом, разбивают данный треугольник на три равновеликих треугольника.
Чтобы вычислить положение центра тяжести по координатам вершин треугольника, достаточно вычислить среднее арифметическое координат вершин по оси x и по оси y, что и делает калькулятор ниже.
- Как определить центр треугольника?
- Как найти середину у треугольника?
- Как найти центр тяжести в треугольнике?
- Как найти центр тяжести в прямоугольном треугольнике?
- Как найти Инцентр?
- Как найти центр тяжести тела неправильной формы?
- Где находится центр тяжести призмы?
- Где находится центр тяжести у кольца?
- Как найти Центроид фигуры?
- Где находится центр тяжести однородного треугольника?
- Где находится центр тяжести у трапеции?
- Как найти центр масс треугольника?
- Как найти длину медианы в прямоугольном треугольнике?
- Где находится центр круга?
- Где лежит центр равнобедренного треугольника?
- Где лежит центр окружности?
- Центры тяжести многоугольников и многогранников
- Двумерный случай: многоугольники
- Центр масс системы точек
- Центр масс каркаса
- Центр масс сплошной фигуры
- Случай треугольника
- Случай треугольника: доказательство
- Случай многоугольника
- Случай многоугольника: альтернативный способ
- Трёхмерный случай: многогранники
- Центр масс системы точек
- Центр масс каркаса многогранника
- Центр масс поверхности многогранника
- Центр масс сплошного многогранника
- Случай тетраэдра
- Случай произвольного многогранника
- 🔥 Видео
Видео:Определение центра тяжести сложной фигуры. СопроматСкачать

Как определить центр треугольника?
Видео:Видеоурок 3. Определение центра тяжести.Скачать

Как найти середину у треугольника?
Пересекающиеся медианы Найдите середину одной стороны треугольника. Для этого измерьте сторону и разделите ее длину пополам. Середину отметьте точкой A.
Видео:Центр тяжести треугольникаСкачать

Как найти центр тяжести в треугольнике?
Центроид треугольника (также барицентр треугольника и центр тяжести треугольника) — точка пересечения медиан в треугольнике. . Центроид треугольника относится к замечательным точкам треугольника и он перечислен в энциклопедии центров треугольника Кларка Кимберлинга, как точка X(2).
Видео:Практическая №5 Определение центра тяжести сложной фигурыСкачать

Как найти центр тяжести в прямоугольном треугольнике?
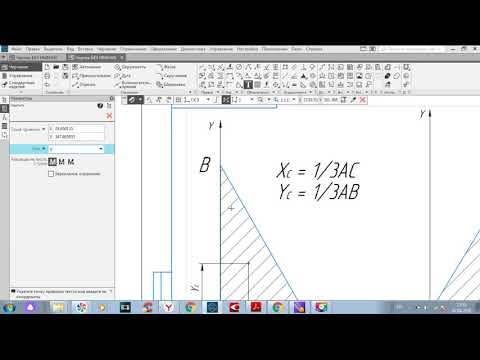
Как найти координаты центра тяжести треугольника?
- Рисуем треугольник ABC.
- Ставим точку M — середина BC.
- Ставим точку H — середина AC.
- Пересечение BH и AM — и есть центр тяжести треугольника ABC.
- Найдем его координаты (координаты точки O (xo, yo, zo) )
Видео:Найдите центр тяжестиСкачать

Как найти Инцентр?
Биссектрисы треугольника пересекаются в одной точке, которая является центром окружности, вписанной в этот треугольник. Инцентр лежит ближе к вершине, расположенной напротив большей стороны треугольника.
Видео:Центры тяжести прямоугольных треугольниковСкачать
Как найти центр тяжести тела неправильной формы?
Центр тяжести тела неправильной формы можно определить так: подвесить его за любую точку, и провести вертикальную линию по отвесу. Затем повернуть тело и повторить операцию. Точка пересечения двух прямых и есть центр тяжести тела.
Видео:Определение центра тяжести сложных сечений. Фигуры из ГОСТ.Скачать

Где находится центр тяжести призмы?
Так, центр тяжести призмы и цилиндра лежит на середине линии, соединяющей центры тяжести оснований. Центр тяжести шара совпадает с его геометрическим центром. Центр тяжести пирамиды (рис. 18, а) лежит на прямой, соединяющей центр тяжести площади основания с противоположной вершиной на расстоянии /4 высоты от основания.
Видео:7 класс, 18 урок, Свойства равнобедренного треугольникаСкачать

Где находится центр тяжести у кольца?
Так, центр тяжести однородных диска и шара расположен в их центре, однородного цилиндра в точке на середине его оси; однородного параллелепипеда на пересечении его диагоналей и т, д. У всех однородных тел центр тяжести совпадает с центром симметрии. Центр тяжести может находиться вне тела, например, у кольца.
Видео:Определение центра тяжести и статистического момента плоской фигурыСкачать

Как найти Центроид фигуры?
Центроид (барицентр или центр масс) вершин произвольного четырёхугольника лежит в точке пересечения 3-х отрезков: 1-й отрезок соединяет середины диагоналей, два другие — середины противополежащих сторон. Точка пересечения делит все три отрезка пополам.
Видео:Центр тяжести. ЭкспериментСкачать

Где находится центр тяжести однородного треугольника?
Таким образом, центр тяжести треугольника лежит в точке пересечения его медиан, которая, как известно, отделяет от каждой медианы третью часть, считая от соответствующей стороны.
Видео:Техническая механика/Определение центра тяжести сложносоставного сечения (Это понятно?!))Скачать

Где находится центр тяжести у трапеции?
Для произвольной трапеции (то есть она может быть прямоугольной, тупоугольной, равнобокой или любой другой) справедливо то, что центр ее тяжести лежит на прямой, которая соединяет середины оснований трапеции.
Видео:координаты центра тяжести треугольникаСкачать

Как найти центр масс треугольника?
Как найти центр треугольника
Если известны координаты его вершин, найдем сумму трех значений координат «х» и трех значений координат «у». Поделим каждую сумму на 3, получим среднее значение сумм координат «х» и «у», что и будет координатами центра тяжести.
Видео:Определение координат центра тяжести сложной фигуры (плоского сечения)Скачать

Как найти длину медианы в прямоугольном треугольнике?
Медиана, проведенная к гипотенузе прямоугольного треугольника, равняется половине квадратного корня из суммы квадратов катетов.
Видео:Практическая работа по теме: Центр тяжестиСкачать

Где находится центр круга?
Центр вписанной окружности треугольника (инцентр) — одна из замечательных точек треугольника, точка пересечения биссектрис треугольника. Центр вписанной в треугольник окружности также иногда называют инцентром.
Видео:Нахождение площади равнобедренного треугольника при помощи теоремы Пифагора | Геометрия | АлгебраСкачать

Где лежит центр равнобедренного треугольника?
В равнобедренном треугольнике высота, проведенная к основанию, является серединным перпендикуляром. Следовательно, центр описанной около равнобедренного треугольника окружности будет лежать на серединном перпендикуляре, который является и высотой, и медианой, и биссектрисой угла при вершине.
Видео:97 Медианы и центр тяжести треугольникаСкачать

Где лежит центр окружности?
Окружность, проходящая через все три вершины треугольника, называется его описанной окружностью. Центр описанной окружности лежит на пересечении серединных перпендикуляров к сторонам треугольника.
Видео:Центр тяжестиСкачать

Центры тяжести многоугольников и многогранников
Центром тяжести (или центром масс) некоторого тела называется точка, обладающая тем свойством, что если подвесить тело за эту точку, то оно будет сохранять свое положение.
Ниже рассмотрены двумерные и трёхмерные задачи, связанные с поиском различных центров масс — в основном с точки зрения вычислительной геометрии.
В рассмотренных ниже решениях можно выделить два основных факта. Первый — что центр масс системы материальных точек равен среднему их координат, взятых с коэффициентами, пропорциональными их массам. Второй факт — что если мы знаем центры масс двух непересекающихся фигур, то центр масс их объединения будет лежать на отрезке, соединяющем эти два центра, причём он будет делить его в то же отношении, как масса второй фигуры относится к массе первой.
Видео:Определение центра тяжестиСкачать

Двумерный случай: многоугольники
На самом деле, говоря о центре масс двумерной фигуры, можно иметь в виду одну из трёх следующих задач:
- Центр масс системы точек — т.е. вся масса сосредоточена только в вершинах многоугольника.
- Центр масс каркаса — т.е. масса многоугольника сосредоточена на его периметре.
- Центр масс сплошной фигуры — т.е. масса многоугольника распределена по всей его площади.
Каждая из этих задач имеет самостоятельное решение, и будет рассмотрена ниже отдельно.
Центр масс системы точек
Это самая простая из трёх задач, и её решение — известная физическая формула центра масс системы материальных точек:
где 


В частности, если все точки имеют одинаковую массу, то координаты центра масс есть среднее арифметическое координат точек. Для треугольника эта точка называется центроидом и совпадает с точкой пересечения медиан:
Для доказательства этих формул достаточно вспомнить, что равновесие достигается в такой точке 

и, выражая отсюда 
Центр масс каркаса
Будем считать для простоты, что каркас однороден, т.е. его плотность везде одна и та же.
Но тогда каждую сторону многоугольника можно заменить одной точкой — серединой этого отрезка (т.к. центр масс однородного отрезка есть середина этого отрезка), с массой, равной длине этого отрезка.
Теперь мы получили задачу о системе материальных точек, и применяя к ней решение из предыдущего пункта, мы находим:
где 




Для треугольника можно показать следующее утверждение: эта точка является точкой пересечения биссектрис треугольника, образованного серединами сторон исходного треугольника. (чтобы показать это, надо воспользоваться приведённой выше формулой, и затем заметить, что биссектрисы делят стороны получившегося треугольника в тех же соотношениях, что и центры масс этих сторон).
Центр масс сплошной фигуры
Мы считаем, что масса распределена по фигуре однородно, т.е. плотность в каждой точке фигуры равна одному и тому же числу.
Случай треугольника
Утверждается, что для треугольника ответом будет всё тот же центроид, т.е. точка, образованная средним арифметическим координат вершин:
Случай треугольника: доказательство
Приведём здесь элементарное доказательство, не использующее теорию интегралов.
Первым подобное, чисто геометрическое, доказательство привёл Архимед, но оно было весьма сложным, с большим числом геометрических построений. Приведённое здесь доказательство взято из статьи Apostol, Mnatsakanian «Finding Centroids the Easy Way».
Доказательство сводится к тому, чтобы показать, что центр масс треугольника лежит на одной из медиан; повторяя этот процесс ещё дважды, мы тем самым покажем, что центр масс лежит в точке пересечения медиан, которая и есть центроид.
Разобьём данный треугольник 
Четыре получившихся треугольника подобны треугольнику 

Треугольники №1 и №2 вместе образуют параллелограмм, центр масс которого 


Пусть теперь вектор 





Наша цель — показать, что вектора 

Обозначим через 






Искомый центр масс 




Таким образом, вектор от вершины 





Таким образом, мы доказали, что вектора 



Более того, попутно мы доказали, что центроид делит каждую медиану в отношении 
Случай многоугольника
Перейдём теперь к общему случаю — т.е. к случаю мноугоугольника. Для него такие рассуждения уже неприменимы, поэтому сведём задачу к треугольной: а именно, разобьём многоугольник на треугольники (т.е. триангулируем его), найдём центр масс каждого треугольника, а затем найдём центр масс получившихся центров масс треугольников.
Окончательная формула получается следующей:
где 



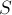
Триангуляция выпуклого многоугольника — тривиальная задача: для этого, например, можно взять треугольники 

Случай многоугольника: альтернативный способ
С другой стороны, применение приведённой формулы не очень удобно для невыпуклых многоугольников, поскольку произвести их триангуляцию — сама по себе непростая задача. Но для таких многоугольников можно придумать более простой подход. А именно, проведём аналогию с тем, как можно искать площадь произвольного многоугольника: выбирается произвольная точка 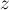


где 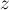
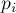



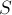

Видео:[How to] Определение центра тяжестиСкачать
![[How to] Определение центра тяжести](https://i.ytimg.com/vi/pGMyMT4a9Ks/0.jpg)
Трёхмерный случай: многогранники
Аналогично двумерному случаю, в 3D можно говорить сразу о четырёх возможных постановках задачи:
- Центр масс системы точек — вершин многогранника.
- Центр масс каркаса — рёбер многогранника.
- Центр масс поверхности — т.е. масса распределена по площади поверхности многогранника.
- Центр масс сплошного многогранника — т.е. масса распределена по всему многограннику.
Центр масс системы точек
Как и в двумерном случае, мы можем применить физическую формулу и получить тот же самый результат:
который в случае равных масс превращается в среднее арифметическое координат всех точек.
Центр масс каркаса многогранника
Аналогично двумерному случаю, мы просто заменяем каждое ребро многогранника материальной точкой, расположенной посередине этого ребра, и с массой, равной длине этого ребра. Получив задачу о материальных точках, мы легко находим её решение как взвешенную сумму координат этих точек.
Центр масс поверхности многогранника
Каждая грань поверхности многогранника — двухмерная фигура, центр масс которой мы умеем искать. Найдя эти центры масс и заменив каждую грань её центром масс, мы получим задачу с материальными точками, которую уже легко решить.
Центр масс сплошного многогранника
Случай тетраэдра
Как и в двумерном случае, решим сначала простейшую задачу — задачу для тетраэдра.
Утверждается, что центр масс тетраэдра совпадает с точкой пересечения его медиан (медианой тетраэдра называется отрезок, проведённый из его вершины в центр масс противоположной грани; таким образом, медиана тетраэдра проходит через вершину и через точку пересечения медиан треугольной грани).
Почему это так? Здесь верны рассуждения, аналогичные двумерному случаю: если мы рассечём тетраэдр на два тетраэдра с помощью плоскости, проходящей через вершину тетраэдра и какую-нибудь медиану противоположной грани, то оба получившихся тетраэдра будут иметь одинаковый объём (т.к. треугольная грань разобьётся медианой на два треугольника равной площади, а высота двух тетраэдров не изменится). Повторяя эти рассуждения несколько раз, получаем, что центр масс лежит на точке пересечения медиан тетраэдра.
Эта точка — точка пересечения медиан тетраэдра — называется его центроидом. Можно показать, что она на самом деле имеет координаты, равные среднему арифметическому координат вершин тетраэдра:
(это можно вывести из того факта, что центроид делит медианы в отношении 
Таким образом, между случаями тетраэдра и треугольника принципиальной разницы нет: точка, равная среднему арифметическому вершин, является центром масс сразу в двух постановках задачи: и когда массы находится только в вершинах, и когда массы распределены по всей площади/объёму. На самом деле, этот результат обобщается на произвольную размерность: центр масс произвольного симплекса (simplex) есть среднее арифметическое координат его вершин.
Случай произвольного многогранника
Перейдём теперь к общему случаю — случаю произвольного многогранника.
Снова, как и в двумерном случае, мы производим сведение этой задачи к уже решённой: разбиваем многогранник на тетраэдры (т.е. производим его тетраэдризацию), находим центр масс каждого из них, и получаем окончательный ответ на задачу в виде взвешенной суммы найденных центров масс.
🔥 Видео
Урок 79. Центр масс тела и методы определения его положенияСкачать













