- Ваш ответ
- решение вопроса
- Похожие вопросы
- Четырехугольник диагонали которого взаимно перпендикулярны вписан в окружность докажите
- Четырёхугольник ABCD, диагонали которого взаимно перпендикулярны, вписан в окружность?
- Точки K и F соответственно середины сторон BC и CD ромба ABCD, в котором угол A = 60градусов , а диагонали пересекаются в точке O ?
- В ромбе ABCD диагонали пересекаются в точке О?
- В трапеции диагонали взаимно перпендикулярны?
- В ромбе ABCD диагонали пересекаются в точке O?
- В1В перпендикуляр к плоскости ромба ABCD, диагонали пересекаются в точке О?
- Четырёхугольник ABCD со сторонами AB = 19 и CD = 28 вписан в окружность?
- Стороны АВ и ВС прямоугольника АВСД равны соответственно 6 и 8?
- Четырехугольник авсд диагонали которого взаимно перпендикулярны вписан в окружность?
- С4 В окружность вписан четырехугольник ABCD, диагонали которого взаимно перпендикулярны и пересекаются в точке Е?
- Помогите решить?
- 📽️ Видео
Видео:№521. Докажите, что если диагонали четырехугольника ABCD взаимно перпендикулярны, то AD2 +ВС2 =AB2+CСкачать

Ваш ответ
Видео:Если в четырёхугольнике диагонали перпендикулярны ... | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать

решение вопроса
Видео:Диагонали четырёхугольника ABCD, вписанного в окружность, взаимно перпендикулярны. Из вершин В и ССкачать
Похожие вопросы
- Все категории
- экономические 43,277
- гуманитарные 33,618
- юридические 17,900
- школьный раздел 606,701
- разное 16,822
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Видео:ОГЭ Задание 24 Площадь выпуклого четырехугольника с перпендикулярными диагоналямиСкачать

Четырехугольник диагонали которого взаимно перпендикулярны вписан в окружность докажите
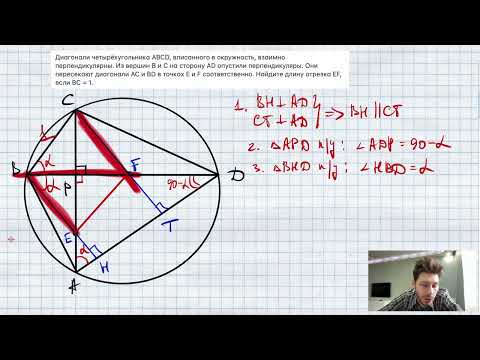
В окружность вписан четырехугольник ABCD, диагонали которого взаимно перпендикулярны и пересекаются в точке E. Прямая, проходящая через точку E и перпендикулярная к AB, пересекает сторону CD в точке M. Известно, что AD = 8, AB = 4, угол CDB равен 60 градусов.
а) Докажите, что EM — медиана треугольника CED.
б) Найдите длину EM.
а) Углы ∠BDC и ∠BAC равны, так как они опираются на одну и ту же дугу BC. Тогда в ΔABE угол ∠ABE = 30° (так как ∠BAC = 60°). Обозначим точку пересечения прямой ME со стороной AB за K. Тогда в прямоугольном треугольнике BKE угол ∠BEK = 60°. Далее, ∠BEK = ∠MED = 60° (как вертикальные). Отсюда получаем, что ΔEDM — равносторонний (так как все углы по 60°), то есть EM = ED = MD
x. Так как в прямоугольном треугольнике CED против угла в 30° лежит катет, в 2 раза меньший гипотенузы, то CD = 2x. Получили, что так как DM = x, точка M является серединой гипотенузы CD, то есть EM — медиана ΔCED. Что и требовалось доказать.
б) Из ΔABE получаем, что Тогда по теореме Пифагора из ΔADE получаем:
Отсюда получаем, что
Ответ:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Имеется верное доказательство утверждения пункта а и обоснованно получен верный ответ в пункте б. | 3 |
| Получен обоснованный ответ в пункте б. Имеется верное доказательство утверждения пункта а и при обоснованном решении пункта б получен неверный ответ из-за арифметической ошибки. | 2 |
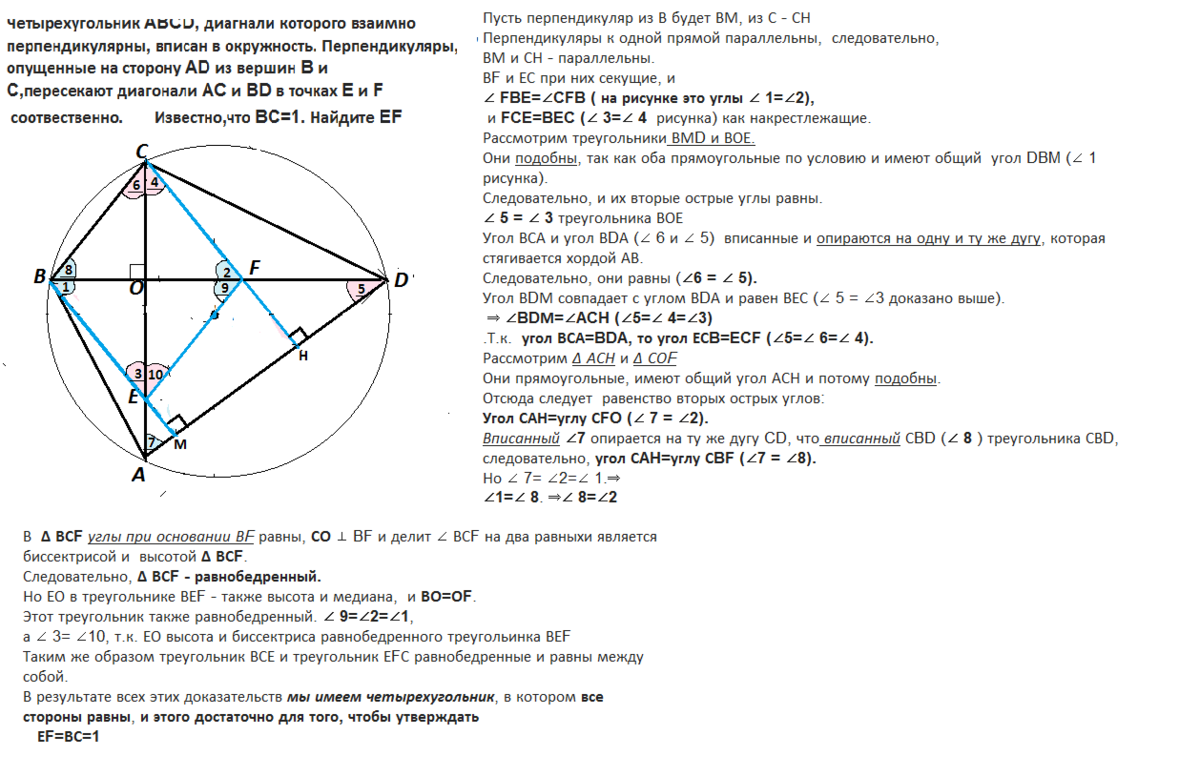
| Имеется верное доказательство утверждения пункта а. При обоснованном решении пункта б получен неверный ответ из-за арифметической ошибки. Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать  Четырёхугольник ABCD, диагонали которого взаимно перпендикулярны, вписан в окружность?Геометрия | 5 — 9 классы Четырёхугольник ABCD, диагонали которого взаимно перпендикулярны, вписан в окружность. Перпендикуляры, опущенные на сторону AD из вершин B и C, пересекают диагонали AC и BD в точках E и F соответственно. Известно, что BC = 1. Пусть перпендикуляр из В будет ВМ, из С — СН Перпендикуляры к одной прямой параллельны, следовательно, ВМ и СН — параллельны. ВF и ЕС при них секущие, и ∠FBE = ∠CFB ( на рисунке это углы∠1 = ∠2), иFCE = BEC (∠ 3 = ∠4 рисунка)как накрестлежащие. Рассмотрим треугольникиВМD и ВОЕ. Ониподобны, так как оба прямоугольные по условию и имеют общий угол DBM (∠1 рисунка). Следовательно, и их вторые острые углы равны. ∠5 = ∠3треугольника ВОЕ Угол ВСА и угол ВDА (∠6 и ∠5) вписанные иопираются на одну и ту же дугу, которая стягивается хордой АВ. Следовательно, они равны (∠6 = ∠5). Угол ВDМ совпадает с углом ВDА и равен ВЕС (∠5 = ∠3 доказано выше). ⇒∠BDМ = ∠ACH (∠5 = ∠4 = ∠3) Угол ВСА = BDA, то угол ЕСB = ECF(∠5 = ∠6 = ∠ 4). Они прямоугольные, имеют общий угол АСН и потомуподобны. Отсюда следует равенство вторых острых углов : Угол САН = углу СFO (∠7 = ∠2). Вписанный∠7опирается на ту же дугу CD, чтовписанныйСBD(∠8)треугольника СВD, следовательно, угол СAH = углу СBF(∠7 = ∠8). В ΔВСFуглы при основании ВFравны, СО⊥ BF иделит ∠ВСF на два равныхи является биссектрисой и высотойΔВСF. Следовательно, ΔВСF — равнобедренный. Но ЕО в треугольнике ВЕF — также высота и медиана, иВО = ОF. Этот треугольник также равнобедренный. К. ЕО высота и биссектриса равнобедренного треугольинка ВЕF Таким же образом треугольник ВСЕ и треугольник ЕFС равнобедренные и равны между собой. В результате всех этих доказательствмы имеем четырехугольник, в которомвсе стороны равны, и этого достаточно для того, чтобы утверждать равенствоЕF = ВС = 1 ( Даны 2 рисунка — один с решением, другой — без) — — — — — — — — — — — —
Видео:№478. В выпуклом четырехугольнике диагонали взаимно перпендикулярны. Докажите, что площадьСкачать 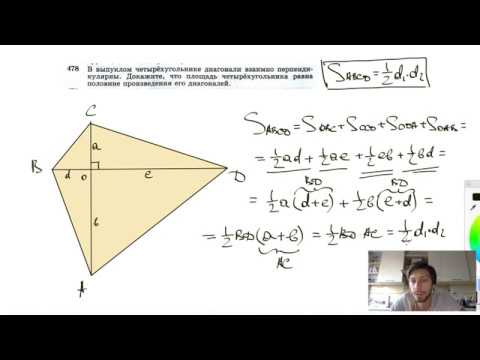 Точки K и F соответственно середины сторон BC и CD ромба ABCD, в котором угол A = 60градусов , а диагонали пересекаются в точке O ?Точки K и F соответственно середины сторон BC и CD ромба ABCD, в котором угол A = 60градусов , а диагонали пересекаются в точке O . Докажите , что диагонали четырехугольника KFDO взаимно перпендикулярны. Видео:3 правила для вписанного четырехугольника #shortsСкачать  В ромбе ABCD диагонали пересекаются в точке О?В ромбе ABCD диагонали пересекаются в точке О. OM, OK, OE перпендикуляры , опущенные на стороны AB, BC, CD соответственно. Докажите, что OM = OK и найдите сумму углов MOB и COE. Видео:Геометрия Диагонали четырехугольника ABCD вписанного в окружность перпендикулярны, угол ACB = 10Скачать  В трапеции диагонали взаимно перпендикулярны?В трапеции диагонали взаимно перпендикулярны. Можно ли в нее вписать окружность? Видео:Вписанная и описанная окружность - от bezbotvyСкачать  В ромбе ABCD диагонали пересекаются в точке O?В ромбе ABCD диагонали пересекаются в точке O. OM, OK, OE – перпендикуляры, опущенные на стороны AB, BС, CD соответственно. Докажите, что OM = OK и найдите сумму углов MOB и COE. Видео:Вписанный четырёхугольник | ЕГЭ-2018. Задание 16. Математика. Профильный уровень | Борис ТрушинСкачать  В1В перпендикуляр к плоскости ромба ABCD, диагонали пересекаются в точке О?В1В перпендикуляр к плоскости ромба ABCD, диагонали пересекаются в точке О. Докажите перпендикулярность прямой AC и плоскости B1OB. Видео:Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать  Четырёхугольник ABCD со сторонами AB = 19 и CD = 28 вписан в окружность?Четырёхугольник ABCD со сторонами AB = 19 и CD = 28 вписан в окружность. Диагонали AC и BD пересекаются в точке K , причём ∠AKB = 60∘ . Найдите радиус окружности, описанной около этого четырёхугольника. Видео:Геометрия Докажите, что площадь выпуклого четырехугольника диагонали которого перпендикулярны равнаСкачать  Стороны АВ и ВС прямоугольника АВСД равны соответственно 6 и 8?Стороны АВ и ВС прямоугольника АВСД равны соответственно 6 и 8. Перпендикуляр, проведенный из вершины С к диагонали ВД, пересекает сторону АД в точке М, а диагональ ВД — в точке К. Найдите площадь четырёхугольника АВКМ. Видео:№950. Докажите, что четырехугольник MNPQ является параллелограммом,Скачать  Четырехугольник авсд диагонали которого взаимно перпендикулярны вписан в окружность?Четырехугольник авсд диагонали которого взаимно перпендикулярны вписан в окружность. Перпендикуляры, опущенные на сторону АД из вершины В и С, пересекают диагонали АС и ВД в точках Е и F соответственно. Известно, что ВС = 1. Видео:Параллельные прямые | Математика | TutorOnlineСкачать  С4 В окружность вписан четырехугольник ABCD, диагонали которого взаимно перпендикулярны и пересекаются в точке Е?С4 В окружность вписан четырехугольник ABCD, диагонали которого взаимно перпендикулярны и пересекаются в точке Е. Прямая, проходящая через точку Е и перпендикулярная к АВ, пересекает сторону CD в точке М. А) Докажите, что ЕМ – медиана треугольника CED. Б) Найдите ЕМ, если AD = 8 , AB = 4 и угол CDB равен 60. Видео:Вписанные четырехугольники. 9 класс.Скачать  Помогите решить?Вершины четырёхугольника ABCD являются серединами сторон четырехугольника , диагонали которого равны по 6 дм и пересекаются под углом 60°. Вычислите площадь четырёхугольника ABCD. На этой странице сайта вы найдете ответы на вопрос Четырёхугольник ABCD, диагонали которого взаимно перпендикулярны, вписан в окружность?, относящийся к категории Геометрия. Сложность вопроса соответствует базовым знаниям учеников 5 — 9 классов. Для получения дополнительной информации найдите другие вопросы, относящимися к данной тематике, с помощью поисковой системы. Или сформулируйте новый вопрос: нажмите кнопку вверху страницы, и задайте нужный запрос с помощью ключевых слов, отвечающих вашим критериям. Общайтесь с посетителями страницы, обсуждайте тему. Возможно, их ответы помогут найти нужную информацию. 📽️ ВидеоГеометрия Доказательство Диагонали ромба перпендикулярны и являются биссектрисами его угловСкачать  8 класс, 3 урок, ЧетырехугольникСкачать  Вписанный в окружность четырёхугольник.Скачать  №43. Докажите, что середины сторон пространственного четырехугольника* являютсяСкачать  №382. Диагонали параллелограмма ABCD пересекаются в точке О. Докажите, что четырехугольникСкачать  |