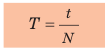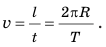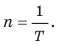Материальная точка равномерно движется по окружности. В момент времени точка была расположена и двигалась так, как показано на рисунке. Установите соответствие между графиками и физическими величинами, зависимость которых от времени эти графики могут представлять. К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.
| ГРАФИКИ | ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ |
Положение тела на окружности можно задавать при помощи угла между положительным направлением оси OX и направлением на тело. Поскольку материальная точка двигается по окружности равномерно, а в начальный момент времени, как видно из рисунка, угол
был равен нулю, заключаем, что закон изменения угла со временем имеет вид
где
постоянный коэффициент, угловая скорость. Глядя на рисунок, легко получить связь угла
с декартовыми координатами точки:
здесь R — радиус окружности. Следовательно, при равномерном вращении тела по окружности, его координаты изменяются по гармоническому закону.
Используя формулы, связывающие законы изменения со временем координаты, скорости, ускорения тела при колебаниях (или взяв соответствующие производные), для законов изменения проекции скоростей и ускорений на оси OX и OY имеем:
1) скорости: ;
2) ускорения:
Обратимся к графикам, приведенным в условии. На графике А физическая величина совершает гармонические колебания, при этом в нулевой момент времени она равна нулю и убывает, то есть закон ее изменения пропорционален Ясно, что из приведенных вариантов ответа это может быть только график проекции скорости тела на ось OX (А — 1).
На графике Б физическая величина совершает гармонические колебания, при этом в начальный момент времени, ее значение равно нулю и возрастает. Ясно, что это может быть только проекция ускорения на ось OY (Б — 4).
- Равномерное движение материальной точки по окружности в физике с примерами
- Движение по окружности
- Определение периода вращения
- Определение частоты вращения
- Как возникли единицы времени: сутки и неделя
- Определяем скорость равномерного движения по окружности
- Точка движется равномерно со скоростью v по окружности радиусом R и в момент времени, принятый за начальный (t=0), занимает положение,
- Ваш ответ
- решение вопроса
- Похожие вопросы
- 🔥 Видео
Видео:Материальная точка равномерно движется по окружности. В момент времени точка была - №23481Скачать

Равномерное движение материальной точки по окружности в физике с примерами
Содержание:
Равномерное движение материальной точки по окружности:
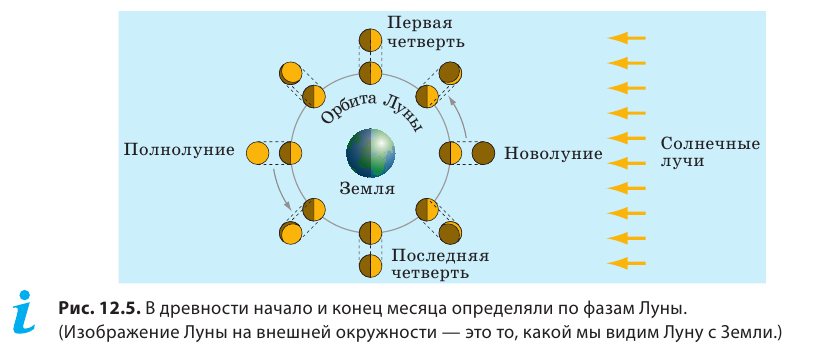
Более 5000 лет назад жрецы древнего Вавилона, наблюдая за Луной, определили такой хорошо известный нам интервал времени, как неделя. Как они это сделали? В чем особенность движения Луны? Встречается ли на Земле подобное движение?
Видео:Движение материальной точки по окружности | Физика ЕГЭ, ЦТСкачать

Движение по окружности
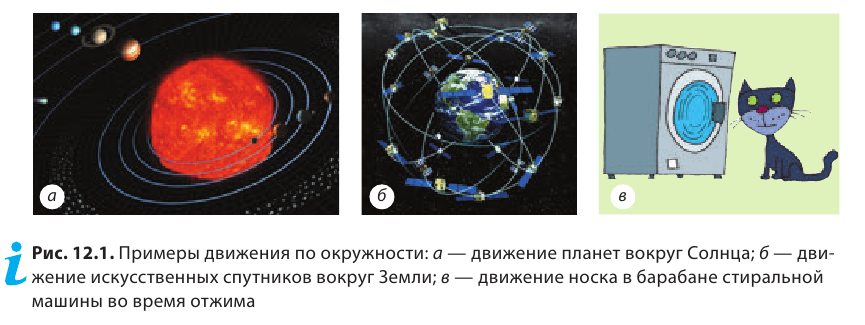
Попробуйте представить линию, вдоль которой движутся ребенок, кружащийся на карусели, носок в барабане стиральной машины во время отжима, кончик ножа блендера при изготовлении коктейля или смузи. Уверены, что вы легко определили: этой линией является окружность. Итак, в перечисленных случаях имеем дело с движением по окружности; простейшим является равномерное движение по окружности. Далее, говоря о равномерном движении по окружности любого физического тела, будем считать это тело материальной точкой. Равномерно по окружности движутся, например, кабинки колеса обозрения. Близким к равномерному движению по окружности является движение планет вокруг Солнца (рис. 12.1, а), естественного спутника (Луны) или искусственных спутников вокруг Земли* (рис. 12.1, б). Приведите примеры движения по окружности. В каких случаях это движение можно считать равномерным? Можно ли считать движение точек обода колеса велосипеда относительно его рамы равномерным движением по окружности? Обоснуйте свой ответ.
Равномерное движение материальной точки по окружности — это такое криволинейное движение, при котором точка, двигаясь по круговой траектории, за любые равные интервалы времени проходит одинаковый путь.
Определение периода вращения
Равномерное движение по окружности — это периодическое движение, то есть движение, повторяющееся через определенные равные интервалы времени. Например, кончик секундной стрелки часов, двигаясь равномерно вдоль циферблата, повторяет свое движение через каждые 60 с (рис. 12.2).
Любое периодическое движение характеризуется такими физическими величинами, как период и частота. При равномерном движении по окружности говорят о периоде вращения и частоте вращения.
Период вращения — это физическая величина, равная времени, за которое материальная точка, равномерно движущаяся по окружности, совершает один оборот. Период вращения обозначают символом T. Единица периода вращения в СИ — секунда: [T]=c. Период вращения равен одной секунде, если за одну секунду совершается один оборот. Кончик секундной стрелки часов совершает один оборот за 60 с, поэтому период его вращения, как и каждой точки секундной стрелки, равен 60 с T =(60c .) Подумайте, каковы периоды вращения точек минутной и часовой стрелок часов. Когда взбивают молочный коктейль блендером, каждая точка его ножа за 30 с делает 6000 оборотов (рис. 12.3). Чтобы определить время одного оборота, нужно время вращения (t = 30 с) разделить на количество оборотов за это время (N = 6000): 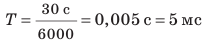
Определение частоты вращения
Указывая технические характеристики устройств, используют не период вращения, а частоту вращения (рис. 12.4). Частота вращения — это физическая величина, которая равна количеству оборотов за единицу времени. Частоту вращения обозначают символом n и определяют по формуле: 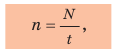
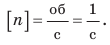
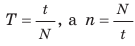
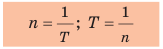
Как возникли единицы времени: сутки и неделя
Как измерить время? Ответ на этот вопрос подсказала людям сама природа. Дело в том, что многие движения, происходящие в природе, являются периодическими, а период такого движения может служить единицей времени. Например, вращение Земли вокруг своей оси — периодическое движение. Ежедневный восход (закат) Солнца, обусловленный этим движением, подсказал нашим предкам единицу времени сутки, которые равны периоду вращения Земли вокруг своей оси. Несколько единиц времени были получены в древнем Вавилоне. Наблюдая за ночным небом, жрецы заметили, что «молодая» Луна появляется на небосклоне приблизительно каждые 28 суток. Периодическое рождение лунного диска служило своего рода вечными «часами». Так возникла единица времени месяц*. За это время Луна, вращаясь вокруг Земли, проходит полный цикл изменения фаз: новолуние, первая четверть, полнолуние, последняя четверть (рис. 12.5). Именно поэтому жрецы разделили лунный месяц на четыре части (поколичеству лунных фаз) и получили семь дней — единицу времени, которая называется неделя.
Определяем скорость равномерного движения по окружности
Кроме периода вращения и его частоты важной характеристикой движения по окружности является скорость движения. Если тело равномерно движется по окружности, то за время, равное периоду вращения t(=T, )тело совершает один оборот, то есть проходит путь, равный длине окружности. Длину окружности l можно вычислить по известной вам из математики формуле: 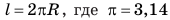
Сейчас, как правило, используют понятие календарного месяца, который не зависит от фаз Луны и длится от 28 до 31 суток.
Именно об этой скорости идет речь, когда, например, определяют скорость движения человека, кружащегося на карусели, говорят о скорости полета искусственных спутников Земли и т. д.
Итоги:
Равномерное движение материальной точки по окружности — это такое криволинейное движение, при котором точка, двигаясь по круговой траектории, за любые равные интервалы времени проходит одинаковый путь. Равномерное движение по окружности — это периодическое движение, то есть движение, повторяющееся через определенные одинаковые интервалы времени. Период вращения T — физическая величина, равная времени, в течение которого материальная точка, равномерно движущаяся по окружности, совершает один оборот. Единица периода вращения в СИ — секунда (с). Частота вращения n — это физическая величина, которая равна количеству оборотов за единицу времени. Единица частоты вращения в СИ — оборот в секунду (об/с, или 1/с). Период вращения T и частоту вращения n определяют по формулам: 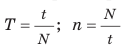
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Колебательное движение
- Физический и математический маятники
- Пружинные и математические маятники
- Скалярные и векторные величины и действия над ними
- Равномерное и неравномерное движение
- Равномерное движение
- Неравномерное движение
- Вращательное движение тела
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Физика - движение по окружностиСкачать

Точка движется равномерно со скоростью v по окружности радиусом R и в момент времени, принятый за начальный (t=0), занимает положение,
Видео:ЕГЭ Физика 2020. Движение по окружности. Задание 7 #3Скачать

Ваш ответ
Видео:Физика | Равномерное движение по окружностиСкачать

решение вопроса
Видео:Криволинейное, равномерное движение материальной точки по окружности. 9 класс.Скачать

Похожие вопросы
- Все категории
- экономические 43,282
- гуманитарные 33,619
- юридические 17,900
- школьный раздел 606,989
- разное 16,829
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
🔥 Видео
Равномерное движение точки по окружности | Физика 10 класс #7 | ИнфоурокСкачать

Физика 10 класс (Урок№4 - Равномерное движение точки по окружности.)Скачать

Точка движется по окружности радиусом R=2см. Волькенштейн 1.47Скачать

Центростремительное ускорение. 9 класс.Скачать

Урок 43. Криволинейное движение. Равномерное движение по окружности. Центростремительное ускорениеСкачать

Криволинейное, равномерное движение материальной точки по окружности. Практическая часть. 9 класс.Скачать

Движение тела по окружности с постоянной по модулю скоростью | Физика 9 класс #18 | ИнфоурокСкачать

ФИЗИКА 10 класс : Механическое движение | Материальная точка, траектория, перемещение.Скачать

Физика 10 Равномерное движение точки по окружностиСкачать

Динамика равномерного движения материальной точки по окружности. Видеоурок 11. Физика 9 классСкачать

№ 1-100 - Физика 10-11 класс РымкевичСкачать

Решение графических задач на равномерное движениеСкачать

КРИВОЛИНЕЙНОЕ ДВИЖЕНИЕ - Угловое Перемещение, Угловая Скорость, Центростремительное УскорениеСкачать

Вращательное движение. 10 класс.Скачать