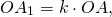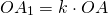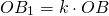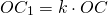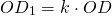Гомотетия и подобия треугольников (8 видео)

Гомотетия

Гомотетия — это преобразование, при котором каждой точке A ставится в соответствие точка A1, лежащая на прямой OA, по правилу

где k — постоянное, отличное от нуля число, O — фиксированная точка.

Точка O называется центром гомотетии, число k — коэффициентом гомотетии.

гомотетия с коэффициентом k>0

Чтобы построить четырёхугольник, гомотетичный 4-угольнику ABCD с центром гомотетии в точке O и коэффициентом k, k>0, нужно провести лучи с началом в точке O, проходящие через вершины A, B, C, D, отложить на них отрезки соответствующей длины:

и соединить вершины A1, B1, C1и D1 отрезками.

При k

и соединить вершины A1, B1, C1 отрезками.

При гомотетии с коэффициентом k=1 каждая точка переводится сама в себя.

При k= -1 гомотетия является симметрией относительно центра O (то есть центральная симметрия является частным случаем гомотетии).

Гомотетия есть преобразование подобия. Следовательно, гомотетия обладает свойствами подобия.

Свойства преобразования гомотетии

1) При гомотетии прямые переходят в прямые, полупрямые- в полупрямые, отрезки — в отрезки, углы — в углы.

2) Сохраняются углы между полупрямыми (соответственно, сохраняется параллельность прямых).

Стороны гомотетичных фигур пропорциональны. а углы — равны.

Содержание

Конспект по теме «Подобие треугольников. Гомотетия»
Краткое описание документа:
Гомотетия. Подобные фигуры. Признаки подобия треугольников, подобие прямоугольных треугольников
🔍 Видео

Видео:ГомотетияСкачать

Конспект по теме «Подобие треугольников. Гомотетия»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

«Актуальность создания школьных служб примирения/медиации в образовательных организациях»

Свидетельство и скидка на обучение каждому участнику

Преобразование подобия. Подобные фигуры

Параллельный перенос симметрии относительно точки, относительно прямой и поворот вокруг точки отображают фигуры в равные им фигуры.

Преобразование, при котором фигура сохраняет вид, но изменяет размеры, называется преобразованием подобия.

Размеры фигуры 1, подобной фигуре 2, могут быть в к раз меньше соответствующих размеров фигуры 1. Число к называется коэффициентом подобия.

Если любой точке Х на плоскости будет соответствовать точка Х ₁ , удовлетворяющая равенству = , то такое преобразование называется гомотетией.

В гомотетии возможно к Точка О называется центром, к- коэффициент гомотетии.

Теорема: В гомотетии с коэффициентом к каждый вектор удлиняется (уменьшается) в к раз.

Теорема: Преобразование подобия сохраняет углы между лучам.

Если треугольники АВС и А ₁ В ₁ С ₁ подобны, то соответствующие углы этих треугольников равны между собой и соответствующие стороны – пропорциональны

1 признак: Если два угла одного треугольника, соответственно равны двум углам другого треугольника, то такие треугольники подобны

2 признак: Если две стороны одного треугольника пропорциональны соответственно двум сторонам другого треугольника и углы, образованные этими сторонами, равны, то такие треугольники подобны

3 признак: Если три стороны одного треугольника пропорциональны соответственно трем сторонам другого треугольника, то эти треугольники подобны

Преобразование подобия. Подобные фигуры

В гомотетии возможно к Точка О называется центром, к- коэффициент гомотетии.

Теорема: В гомотетии с коэффициентом к каждый вектор удлиняется (уменьшается) в к раз.

Теорема: Преобразование подобия сохраняет углы между лучам.

Краткое описание документа:

Подобие есть взаимно однозначное отображение евклидова пространства на себя.
Подобие сохраняет порядок точек на прямой, то есть если точка лежит между точками , и , , — соответствующие их образы при некотором подобии, то также лежит между точками и .
Точки, не лежащие на прямой, при любом подобии переходят в точки, не лежащие на одной прямой.
Подобие преобразует прямую в прямую, отрезок в отрезок, луч в луч, угол в угол, окружность в окружность.
При подобии угол сохраняет величину.
Подобие с коэффициентом , преобразующее каждую прямую в параллельную ей прямую, является гомотетией с коэффициентом или .
- Каждое подобие можно рассматривать как композицию движения и некоторой гомотетии с положительным коэффициентом.
- Подобие называется собственным (несобственным), если движение является собственным (несобственным). Собственное подобие сохраняет ориентацию фигур, а несобственное — изменяет ориентацию на противоположную.
Два треугольника являются подобными, если
- их соответственные углы равны, или
- стороны пропорциональны. См. также Признаки подобия треугольников.
Площади подобных фигур пропорциональны квадратам их сходственных линий (например, сторон). Так, площади кругов пропорциональны отношению квадратов их диаметров (или радиусов).

Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Гомотетия. Подобные фигуры. Признаки подобия треугольников, подобие прямоугольных треугольников

Подобие – это понятие, характеризующее наличие одинаковой, не зависящей от размеров, формы у геометрических фигур.

Подобные фигуры – это фигуры, для которых существует взаимно-однозначное соответствие, при котором расстояние между любыми парами их соответствующих точек изменяется в одно и то же число раз.

Например, то, что фигуры F₁ и F₂ подобны, означает, что для любых двух точек M₁ и N₁ фигуры F₁ и сопоставленных им точек M₂ и N₂ фигуры F₂ выполняется соответствие (frac=k) , где k – одно и то же число для всех точек (k > 0). Число k называется коэффициентом подобия.Преобразование фигуры F₁ в фигуру F₂, при котором расстояния между точками изменяются в одно и то же число раз, называется преобразованием подобия.

Гомотетия – это преобразование подобия. Это преобразование, в котором получаются подобные фигуры (фигуры, у которых соответствующие углы равны и стороны пропорциональны).

Гомотетия – это преобразование, при котором каждой точке A ставится в соответствие точка A₁, лежащая на прямой OA, по правилу (OA_1=kcdot OA) , где k – постоянное, отличное от нуля число, O – фиксированная точка. Точка O называется центром гомотетии, число k – коэффициентом гомотетии.

Свойства преобразования гомотетии:

1) При гомотетии прямые переходят в прямые, полупрямые – в полупрямые, отрезки – в отрезки, углы – в углы.

2) Сохраняются углы между полупрямыми (соответственно, сохраняется параллельность прямых). Стороны гомотетичных фигур пропорциональны, а углы равны.

Подобные треугольники – это треугольники, у которых углы равны, а стороны пропорциональны.

Свойства подобных треугольников