Вычислить момент инерции треугольника

При выполнении расчетов часто приходится вычислять моменты инерции сложных сечений относительно различных осей, лежащих в плоскости фигуры. Для стандартных поперечных сечений стержней моменты инерции даны в таблицах ГОСТ 8509-93, ГОСТ 8510-86, ГОСТ 57837-2017, ГОСТ 8240-97. В остальных случаях, для выполнения онлайн расчета момента инерции круга, кольца, треугольника, прямоугольного контура, нестандартных сварных швеллера, уголка и двутавра можно воспользоваться данной страницей нашего сайта.

Видео:Моменты инерции для треугольника. Вывод моментов инерции для треугольниковСкачать

Момент инерции треугольника

МОМЕНТ ИНЕРЦИИ ТРЕУГОЛЬНИКА

Момент инерции Ix₀, м 4

Момент инерции Ix₁, м 4

Момент инерции Ix₂, м 4

Площадь сечения F, м 2

©Copyright Кайтек 2020

Момент инерции треугольника относительно центральной оси, параллельной одной из его сторон вычисляется по формуле:
I_x0 = b×h 3 / 36;
Момент инерции треугольника относительно оси, совпадающей с одной из его сторон:
I_x1 = b×h 3 / 12;
Момент инерции треугольника относительно оси, параллельной одной из его сторон и проходящей через противоположную вершину:
I_x2 = b×h 3 / 4.

Видео:Урок 94. Вычисление моментов инерции телСкачать

Момент инерции кольца

МОМЕНТ ИНЕРЦИИ КОЛЬЦА

Момент инерции Ix, м 4

Полярный момент инерции Ip, м 4

Площадь сечения F, м 2

©Copyright Кайтек 2020

Момент инерции кольца относительно главной центральной оси:
I_x = π×D 4 /64 — π×d 4 /64;
Полярный момент инерции кольца:
I_p = π×D 4 /32 — π×d 4 /32.

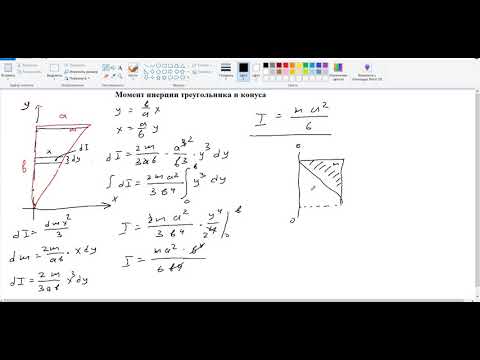
Видео:7. Момент инерции треугольника и конусаСкачать

Момент инерции прямоугольника

МОМЕНТ ИНЕРЦИИ ПРЯМОУГОЛЬНИКА

Момент инерции Ix, м 4

Момент инерции Iy, м 4

Площадь сечения F, м 2

©Copyright Кайтек 2020

Момент инерции прямоугольника относительно главных центральных осей:
I_x = (b×h 3 — b1×h1 3 )/12;
I_y = (h×b 3 — h1×b1 3 )/12.

Видео:Моменты инерции Прямоугольника ► Вывод моментов инерции для прямоугольникаСкачать

Момент инерции двутавра

МОМЕНТ ИНЕРЦИИ ДВУТАВРА

Толщина полки t, мм

Толщина стенки s, мм

Момент инерции Ix, м 4

Момент инерции Iy, м 4

Площадь сечения F, м 2

©Copyright Кайтек 2020

Моменты инерции двутавра относительно главных центральных осей:
I_x = (B×H 3 — (B — s)×(H — 2t) 3 ) / 12;
I_y = (2t×B 3 + (H — 2t)×s 3 ) / 12.

Видео:Моменты инерции сечения из простых фигурСкачать

Момент инерции уголка

МОМЕНТ ИНЕРЦИИ УГОЛКА

Момент инерции Ix, м 4

Момент инерции Iy, м 4

Площадь сечения F, м 2

©Copyright Кайтек 2020

Моменты инерции уголка относительно центральных осей:
I_x = (d×(H — y) 3 + B×y 3 — (B — d)×(y — d) 3 ) / 3;
I_y = (d×(B — x) 3 + H×x 3 — (H — d)×(x — d) 3 ) / 3,
где x и y — расстояния от наружных сторон уголка до центральных осей Y и X соответственно.

Видео:1.256Скачать

Момент инерции швеллера

МОМЕНТ ИНЕРЦИИ ШВЕЛЛЕРА

Толщина полки d, мм

Толщина стенки s, мм

Момент инерции Ix, м 4

Момент инерции Iy, м 4

Площадь сечения F, м 2

©Copyright Кайтек 2020

Моменты инерции швеллера относительно главных центральных осей:
I_x = (B×H 3 — (B — s)×(H-2d) 3 ) / 12;
I_y = (H×x 3 — (H — 2d)×(x — s) 3 + d×(B — x) 3 )/3,
где x — расстояния от наружной сторон швеллера до центральной оси Y.

Расчеты моментов инерции по умолчанию выполнены относительно центральных и главных центральных осей сечения. Моменты инерции относительно осей, параллельных главным центральным осям можно вычислить, прибавив к полученному результату произведение квадрата расстояния между соответствующими осями на площадь сечения.

Видео:Расчёт момента инерции тела относительно оси вращения. Момент инерции однородного стержняСкачать

Механические приложения двойного интеграла

Механические приложения двойного интеграла

1. Услуги проектирования
2. Двойной интеграл
3. Механические приложения двойного интеграла

Видео:Момент инерцииСкачать

Механические приложения двойного интеграла

Будем считать, что $mathbf < textit > $ — неоднородная плоская пластина с поверхностной плотностью материала в точке $P$ равной $mu (P)$. В механике $mu (P)$ определяется так. Точка $P$ окружается малой областью $mathbf < textit > $, находится масса $mathbf < textit > (mathbf < textit > )$ и площадь этой области < площадь тоже будем обозначать буквой $mathbf < textit > $ > и $mu (P)=mathop limits_ frac $.

Для нахождения массы по заданной плотности мы решим обратную задачу. Разобьём $mathbf < textit > $ на малые подобласти $mathbf < textit > _ $, $mathbf < textit > _ $,$mathbf < textit > _ , , mathbf < textit > _ $, в каждой из подобластей $mathbf < textit > _ $ выберем произвольную точку $mathbf < textit

> _ $, и, считая что в пределах $mathbf < textit > _ $ плотность постоянна и равна $mu (P_i )$, получим, что масса $mathbf < textit > _ $ приближённо есть $mu (P_i )cdot s(D_i )$, а масса всей пластины $sumlimits_ ^n $.

Это интегральная сумма, при уменьшении $d=mathop limits_ diam(D_i )$ точность приближения увеличивается, и в пределе $m(D)=mathop limits_ < begin dto 0 \ (nto infty ) \ end > sumlimits_ ^n =iintlimits_D $.

Аналогично находятся другие параметры пластины:

Координаты центра тяжести

Моменты инерции пластины

Пластина расположена в области (R) и ее плотность в точке ( < left( right) > ) равна ( < rho left( right) > ).

Масса пластины

(m = largeiintlimits_Rnormalsize < rho left( right)dA > )

Статические моменты пластины

Момент пластины относительно оси (Ox) определяется формулой

Аналогично, момент пластины относительно оси (Oy) выражается в виде

Координаты центра масс пластины

• (bar x = largefrac < < > >normalsize = largefrac normalsize largeiintlimits_Rnormalsize < xrho left( right)dA > = largefrac < < iintlimits_R < xrho left( right)dA > > >< < iintlimits_R < rho left( right)dA > > > normalsize,;)
• (bar y = largefrac < < > >normalsize = largefrac normalsize largeiintlimits_Rnormalsize < yrho left( right)dA > = largefrac < < iintlimits_R < yrho left( right)dA > > >< < iintlimits_R < rho left( right)dA > > > normalsize ).

Заряд пластины

(Q = largeiintlimits_Rnormalsize < sigma left( right)dA > ),

где электрический заряд распределен по области (R) и его плотность в точке ( < left( right) > ) равна ( < sigma left( right) > ).

Среднее значение функции

(mu = largefrac iintlimits_Rnormalsize < fleft( right)dA > ,;) где (S = largeiintlimits_Rnormalsize ).

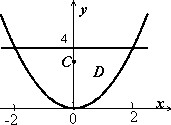
Найти параметры неоднородной плоской пластины, ограниченной кривыми

$D:left[ < begin y=x^2, \ y=4; \ end >right.$ если плотность $mu (x,y)=y+1$.

Решение:

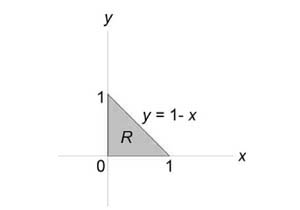
Вычислить моменты инерции треугольника, ограниченного прямыми (x + y = 1,) (x = 0,) (y = 0) и имеющего плотность $rho left( right) = xy.$

Решение:

Электрический заряд распределен по площади диска ( + = 1) таким образом, что его поверхностная плотность равна $sigma left( right) = 1 + + ;left( < text ^2 >right)$ Вычислить полный заряд диска.

Решение:

В полярных координатах область, занятая диском, описывается множеством (left[< left( right)|;0 le r le 1,0 le theta le 2pi >right].)

Далее:

Несобственные интегралы от неограниченной функции

Условия независимости криволинейного интеграла от пути интегрирования

Определение двойного интеграла

Класс M. Теорема о замкнутости класса M

Булевы функции от $n$ переменных

Класс $L$. Теорема о замкнyтости класса $L$

Примеры применения цилиндрических и сферических координат

Несобственные интегралы по неограниченной области

Логические операции над высказываниями

Замыкание. Свойства замыкания. Теорема о сведении к заведомо полной системе

Поток жидкости через поверхность

Механические приложения тройного интеграла

Переход от двойного интеграла к повторному. Изменение порядка интегрирования. Переход к полярным координатам

Класс Te . Теорема о замкнутости Te

Равносильные формулы алгебры высказываний

Огравление $Rightarrow $

Видео:Урок 98. Задачи на вычисление моментов инерции (ч.1)Скачать

Момент инерции сечения

Меня часто спрашивают: «…а что такое моменты инерции в сопротивлении материалов и зачем они вообще?» Об этом в сегодняшней теме

Видео:Теория (часть 1) осевые моменты инерцииСкачать

Моменты инерции сечения из простых фигур

Начнем с моментов инерции простых фигур и на их примере выясним для сложных фигур и составных сечений из стандартных профилей.

Начать объяснение о том, что такое моменты инерции нужно с того, что спросить, а что такое площадь?

Обычная площадь квартиры, огорода сечения стержня? Зачем она и почему?

Так вот площадь это характеристика которую придумали и вывели для разных фигур, чтобы была возможность сравнивать земельные наделы. Не всегда они были прямоугольные или квадратные. А сравнить кто сколько получил в надел было нужно. Вот и вывели такую закономерность для прямоугольника, что если перемножить стороны — получим величину, которую можно будет сравнить с перемноженной высотой на основание деленное пополам для треугольника или для круга Пи умножить на эр в квадрате )). Т.е. площади простых фигур

Что касается моментов инерции в сопротивлении материалов, то тут они появились, когда стало понятно, что есть какая то геометрически измеримая величина для разных форм сечения, которая позволит сравнить сопротивляемость этих сечений изгибу.

Проще говоря бревно, которое выполняет роль балки и изгибается может иметь форму прямоугольника, квадрата или круга, а нам нужно сравнить их сопротивляемость изгибу. Вот для этих целей выводили формулу напряжений и оказалось, что в числителе оказался изгибающий момент, а в знаменателе момент инерции:

на балке изображены главные центральные оси z y

прогибы для таких балок будут разными относительно осей z и y, т.к. моменты инерции будут разные.

Видео:5. Момент инерции простейших телСкачать

Вывод моментов инерции для простых фигур

Так вот ниже я приведу видео уроки, плейлист, в котором один за одним выведены моменты инерции для простых фигур, а именно для прямоугольника, треугольника и круга. А затем приводится стандартный расчет моментов инерции для более сложной фигуры, которая состоит из нескольких простых. Всегда сложную фигуру можно разбить на несколько простых. Исходя из этого расчет и ведется.

Моменты инерции измеряются в единицах длины в 4 степени, т.е. см⁴ или м⁴. Чаще всего используется см⁴, т.к. такие единицы измерения приведены в сортаменте прокатной стали.

Момент инерции, это величина, которая показывает сопротивляемость сечения изгибу. На примере линейки хорошо понятно что изгиб в одной плоскости и изгиб в другой плоскости будут сильно отличаться, хотя площадь сечения не меняется. Вот это и было выведено в формуле для напряжений и для прогибов. Что величина, которая сопротивляется изгибающему моменту есть интеграл до координаты центра тяжести площадки в квадрате на площадь элементарной площадки.

Центральными осями называют оси, которые проходят через центр тяжести сечения

Главные оси располагаются в сечении таким образом, что центробежный момент относительно них равен нулю. Т.е. это максимальный и минимальный осевые моменты инерции

Оси, которые проходят через центр тяжести сечения и центробежный момент инерции относительно них равен нулю. При этом данные осевые моменты инерции являются экстремальными, т.е. имеют максимальное и минимальное значение. Именно относительно этих осей ведут расчет и к ним приводят нагрузки. Т.е. если какое нибудь внешнее усилие проходит в стороне от главных центральных осей. Это усилие переносят соблюдая правила переноса к главным центральным осям. Только после этого рассматривают действие сил и находят внутренние усилия относительно главных центральных осей инерции.

При вычислении моментов инерции осевых, при переходе от одних осей к другим появляется центробежный момент инерции, как составляющая пары осевых моментов инерции. И только для главных осей центробежные моменты инерции равны нулю. Именно эти оси мы и отыскиваем в наших расчетах. Поэтому мы ищем величину центробежного момента инерции для не главных осей и из свойства, что главные центральные оси это такие оси, относительно которых центробежный момент инерции равен нулю, находим положение главных центральных осей.

Видео:Основы сопромата. Задача 4. Момент инерции сложного сеченияСкачать

Моменты инерции для прямоугольника

Видео:Вычисление моментов инерции составного сеченияСкачать

#Сопромат, Моменты инерции. Прямоугольник. Вывод моментов инерции для прямоугольника.

Сопротивление материалов и Моменты инерции для прямоугольника. Понятие моментов инерции, формулы и вывод для прямоугольника. Осевые центробежный моменты инерции. для треугольника вывод моментов инерции в этом видео: https://www.youtube.com/embed/_pixohVoc-4?vq=hd720 Тема моментов инерции возникла в связи стем, что для определения напряжений при изгибе понадобилась геометрическая характеристика, которая сопротивляется внутреннему усилию (изгибающему моменту). В результате вывода формулы напряжений и появилась эта формула, выраженная через интеграл от квадрата координаты помноженной на площадь элементарной площадки. Эту геометрическую характеристику и назвали моментом инерции. пройти полный курс обучения сопромату и строймеху онлайн, по скайпу. Задать вопросы можно: — через сайт: https://stroymex.online — skype: zabolotnyiAN — email: zabolotnyiAN@gmail.com — комменты к видео — Телеграм https://t.me/AleksanderCrafts Телеграм канал: https://t.me/sroymexOnline Не тратьте время зря, задавайте вопросы. Узнайте стоимость обучения: https://stroymex.online/usloviya-i-tsena-onlayn-obucheniya-sopromat-i-stroymeh Получите первую консультацию бесплатно! Facebook: https://www.facebook.com/SopromatOnline

2018-04-09

моменты инерции для прямоугольника для главных центральных осей равны, формула

моменты инерции для прямоугольника для осей проходящих через основные размеры равны, формула

Моменты инерции для треугольника

Видео:Сопротивление материалов. Лекция: геометрические характеристики сечений - моменты инерцииСкачать

Сопротивление материалов, Моменты инерции для треугольника. Сопромат вывод моментов инерции

Сопротивление материалов и Моменты инерции для треугольника. Сопромат вывод моментов инерции для простых фигур. Моменты инерции для треугольника. Моменты инерции для осей в треугольнике, которые проходят через основные размеры. Вывод и пояснение к этой теме сопротивления материалов. для прямоугольника вывод моментов инерции в этом видео: https://www.youtube.com/watch?v=v1TE1UW_sRE&feature=youtu.be‎ Тема моментов инерции возникла в связи стем, что для определения напряжений при изгибе понадобилась геометрическая характеристика, которая сопротивляется внутреннему усилию (изгибающему моменту). В результате вывода формулы напряжений и появилась эта формула, выраженная через интеграл от квадрата координаты помноженной на площадь элементарной площадки. Эту геометрическую характеристику и назвали моментом инерции. пройти полный курс обучения сопромату и строймеху онлайн, по скайпу Задать вопросы можно: — через сайт: https://stroymex.online — skype: zabolotnyiAN — email: zabolotnyiAN@gmail.com — комменты к видео — Телеграм https://t.me/AleksanderCrafts Телеграм канал: https://t.me/sroymexOnline Не тратьте время зря, задавайте вопросы. Узнайте стоимость обучения: https://stroymex.online/usloviya-i-tsena-onlayn-obucheniya-sopromat-i-stroymeh Получите первую консультацию бесплатно! Facebook: https://www.facebook.com/SopromatOnline

2018-04-09

Моменты инерции треугольника относительно произвольых осей

Видео:Определение осевых моментов инерции составного несимметричного сечения. СопроматСкачать

Момент инерции круга. Моменты инерции простых фигур. #сопромат

Вывод моментов инерции для круга. Видео урок из темы «Моменты инерции простых фигур». В видео приведен вывод момента инерции полярного, в полярной системе координат Ip Затем выведены моменты инерции осевые Iz, Iy. Задать вопросы можно: — через сайт: https://stroymex.online — skype: zabolotnyiAN — email: zabolotnyiAN@gmail.com — комменты к видео — Телеграм https://t.me/AleksanderCrafts Телеграм канал: https://t.me/sroymexOnline Не тратьте время зря, задавайте вопросы. Узнайте стоимость обучения: https://stroymex.online/usloviya-i-tsena-onlayn-obucheniya-sopromat-i-stroymeh Получите первую консультацию бесплатно! Facebook: https://www.facebook.com/SopromatOnline

2019-09-14

Видео:Момент инерцииСкачать

Моменты инерции. Оси центральные и главные. Что это и где. #сопромат

Центральные оси — любая пара взаимно перпендикулярных осей, которые проходят через центр тяжести фигуры Главные оси — оси для которых центробежный момент инерции равен нулю, а осевые моменты имеют максимум и минимум. Об этом и многом другом в видео уроке по моментам инерции в сопротивлении материалов Задать вопросы можно: — через сайт: https://stroymex.online — skype: zabolotnyiAN — email: zabolotnyiAN@gmail.com — комменты к видео — Телеграм https://t.me/AleksanderCrafts Телеграм канал: https://t.me/sroymexOnline Не тратьте время зря, задавайте вопросы. Узнайте стоимость обучения: https://stroymex.online/usloviya-i-tsena-onlayn-obucheniya-sopromat-i-stroymeh Получите первую консультацию бесплатно! Facebook: https://www.facebook.com/SopromatOnline

2019-09-14

Видео:Моменты инерции простейших фигур. Оси центральные и главные. Что это и где. #сопроматСкачать

Примеры расчетов моментов инерции для сечений

Ниже приводятся примеры расчетов моментов инерции относительно главных центральных осей, объяснение, что такое центробежный момент инерции и почему оси называются главными центральными для примеров:

• простейшие фигуры — прямоугольник, треугольник
• составные сечения из простейших треугольника и прямоугольника
• составные из прокатных профилей

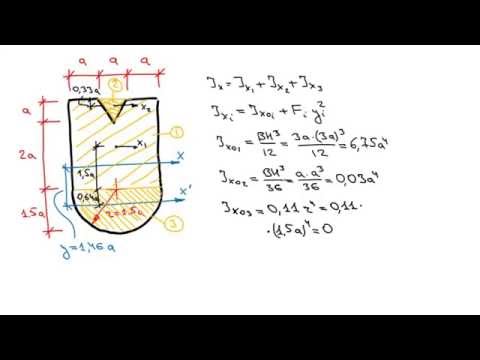
Пример расчета моментов инерции относительно главных центральных осей для простейших фигур

Подробно объясняется как найти центробежный момент инерции, как найти осевые моменты инерции, как относительно центральных и как относительно главных осей для простых фигур.

Пример расчета моментов инерции для сечения состоящего из прямоугольника и треугольника

Сечения балок может быть составным, т.е. таким, которое складывается из нескольких фигур. В примере, в видеоуроке ниже рассказыватся как найти моменты инерции относительно главных центральных осей для такого сечения балки

Расчет моментов инерции сечения составного из стандартных прокатных профилей

В видеоуроке ниже разбирается порядок расчета моментов инерции относительно главных центральных осей для сечения составленого из трех прокатных профилей уголков

📽️ Видео

Геометрические характеристики. Моменты инерции. Радиусы инерции. Сопромат.Скачать

Объем и момент инерции однородного шараСкачать

Моменты инерции относительно Главных Центральных осей для простых фигурСкачать