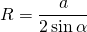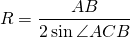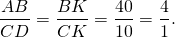Четырехугольник abcd со сторонами ab 39 cd 12 (3 видео)

Четырехугольник abcd со сторонами ab 39 cd 12

Задание 26. Четырёхугольник ABCD со сторонами АВ = 12 и CD = 30 вписан в окружность. Диагонали АС и BD пересекаются в точке K, причём угол AKB = 60°. Найдите радиус окружности, описанной около этого четырёхугольника.

Углы как вертикальные. Проведем отрезок DN параллельный отрезку AC. В этом случае — накрест лежащие при параллельных прямых AC и DN и секущей BD.

Четырехугольник DNAB вписан в окружность, следовательно,

Далее, как накрест лежащие при параллельных прямых AC, DN и секущей AD, следовательно, дуга AN равна дуге DC, откуда AN=DC=30.

Рассмотрим треугольник NAB вписанный в окружность. По теореме косинусов, имеем:

По теореме синусов можно записать:

где R – радиус описанной окружности. Из последнего выражения:

Содержание

Задачи №26 на ГИА по математике материал для подготовки к егэ (гиа) по геометрии (9 класс) на тему
Скачать:
Предварительный просмотр:
По теме: методические разработки, презентации и конспекты
Четырехугольник ABCD вписан в окружность
📹 Видео

Видео:Четырёхугольник ABCD со сторонами AB = 40 и CD = 10 вписан в окружность. Диагонали #огэ #математикаСкачать

Задачи №26 на ГИА по математике
материал для подготовки к егэ (гиа) по геометрии (9 класс) на тему

В работе представлена подборка из 40 задач по геометрии повышенного уровня сложности из Открытого Банка заданий ГИ А с подробными решениями и хорошими чертежами. Материал может быть полезен как для учителей математики так и для учащихся.

Видео:В четырехугольник ABCD вписана окружность, AB = 10, BC = 11 и CD = 15. Найдите четвертую сторону.Скачать

Скачать:

Вложение	Размер
zadachi_no_26_na_gia_po_matematike.docx	306.8 КБ

Бесплатный марафон подготовки к ЕГЭ на зимних каникулах

Учи.Дома запускает бесплатный марафон в котором каждый день. В течении 5 дней утром ты будешь получать одно задание по выбранному предмету, а вечером его решение. Твоя задача, успеть выполнение задание до того как получишь ответ.

Бесплатно, онлайн, подготовка к ЕГЭ

Видео:Урок 2. Описанная окружность около четырехугольника. Задача из ОГЭ| Подобные треугольникиСкачать

Предварительный просмотр:

Задание №361445 стр.32

Четырёхугольник ABCD со сторонами AB =25 и CD =16 вписан в окружность. Диагонали AC и BD пересекаются в точке K , причём ∠ AKB =60 ∘ . Найдите радиус окружности, описанной около этого четырёхугольника

Проведём BF ║АС, тогда четырёхугольник АВСD – равнобедренная трапеция,

∠ DBC = ∠ DKC (по свойству соответственных углов при BF║AC и секущей BD).

В вписанном четырёхугольнике DBFC ∠ DCF = 180° — ∠ DBF

Из треугольника DCF по теореме косинусов имеем: DF 2 = 25 2 + 16 2 + 2 ∙16 ∙25∙ 0,5.

Из треугольника DВF: 2R = = 2 ; R = .

Четырёхугольник ABCD со сторонами AB =5 и CD =17 вписан в окружность. Диагонали AC и BD пересекаются в точке K , причём ∠ AKB =60 ∘ . Найдите радиус окружности, описанной около этого четырёхугольника.

Четырёхугольник ABCD со сторонами AB =39 и CD =12 вписан в окружность. Диагонали AC и BD пересекаются в точке K , причём ∠ AKB =60° . Найдите радиус окружности, описанной около этого четырёхугольника.

Четырёхугольник ABCD со сторонами AB =43 и CD =4 вписан в окружность. Диагонали AC и BD пересекаются в точке K , причём ∠ AKB =60 ∘ . Найдите радиус окружности, описанной около этого четырёхугольника.

Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K . Найдите площадь параллелограмма, если BC =19 , а расстояние от точки K до стороны AB равно 7.

По свойству биссектрис углов параллелограмма ABM и ABN равнобедренные:

AB = BM и AB = AN, следовательно BM = AN.

Так как BM = AN и BM ║ AN, то четырёхугольник ABMN – параллелограмм, а так как AB = AN, то ABMN – ромб.

По свойству ромба ABК = MКВ = AKN (по двум катетам),

тогда KP = KS = KT = 7(как высоты равных треугольников, проведённые к соответственно равным сторонам).

Отрезки KP и KS лежат на одной прямой, ST — высота параллелограмма ABCD,

ST = SK + KT; ST = 7 + 7 =14

S ABCD = AD ∙ ST; S ABCD = 19 ∙ 7=133

Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K . Найдите площадь параллелограмма, если BC =11 , а расстояние от точки K до стороны AB равно 3.

Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K . Найдите площадь параллелограмма, если BC =12 , а расстояние от точки K до стороны AB равно 9.

Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K . Найдите площадь параллелограмма, если BC =19 , а расстояние от точки K до стороны AB равно 10.

На стороне BC остроугольного треугольника ABC ( AB ≠ AC ) как на диаметре построена полуокружность, пересекающая высоту AD в точке M , AD =90 , MD =69 , H — точка пересечения высот треугольника ABC . Найдите AH .

Проведем ВЕ. Так как ВС – диаметр, то ∠ ВАС =90 ̊ , следовательно ВЕ – высота и

По свойству отрезков секущих АЕ ∙АС = АМ ∙АК.

АМ = AD – MD, AM = 90 – 69 = 21

Так как хорда МК перпендикулярна диаметру ВС, то MD = DK = 69.

AK = AM + MD + DK, AK = 21+ 69 + 69 = 159.

AEH (по двум углам: А – общий угол, углы ADC и AEH –прямые)

На стороне BC остроугольного треугольника ABC ( AB ≠ AC ) как на диаметре построена полуокружность, пересекающая высоту AD в точке M , AD =49 , MD =42 , H — точка пересечения высот треугольника ABC . Найдите AH .

На стороне BC остроугольного треугольника ABC ( AB ≠ AC ) как на диаметре построена полуокружность, пересекающая высоту AD в точке M , AD =27 , MD =18 , H — точка пересечения высот треугольника ABC . Найдите AH .

На стороне BC остроугольного треугольника ABC ( AB ≠ AC ) как на диаметре построена полуокружность, пересекающая высоту AD в точке M , AD =63 , MD =21 , H — точка пересечения высот треугольника ABC . Найдите AH .

Окружность пересекает стороны AB и AC треугольника ABC в точках K и P соответственно и проходит через вершины B и C . Найдите длину отрезка KP , если AP =7 , а сторона BC в 1,4 раза меньше стороны AB .
Решение:

АВР и АСК подобны (по двум углам, А – общий угол, углы АВР и АСК – вписанные, опираются на дугу РК), значит или

Тогда АВС и АРК подобны (по двум сторонам и углу между ними, так как , А – угол заключенный между пропорциональными сторонами), следовательно ;

Окружность пересекает стороны AB и AC треугольника ABC в точках K и P соответственно и проходит через вершины B и C . Найдите длину отрезка KP , если AK =21 , а сторона AC в 1,5 раза больше стороны BC .

Окружность пересекает стороны AB и AC треугольника ABC в точках K и P соответственно и проходит через вершины B и C . Найдите длину отрезка KP , если AK =9 , а сторона AC в 3 раза больше стороны BC .

Окружность пересекает стороны AB и AC треугольника ABC в точках K и P соответственно и проходит через вершины B и C . Найдите длину отрезка KP , если AP =6 , а сторона BC в 1,5 раза меньше стороны AB .

Из вершины прямого угла C треугольника ABC проведена высота CP . Радиус окружности, вписанной в треугольник BCP , равен 60, тангенс угла BAC равен . Найдите радиус окружности, вписанной в треугольник ABC .

САР = ВСР, тогда tg ∠ BCP = =

Пусть BP = 4x, CP = 3x, тогда BC = 5x

R BCP = = = x, x = 60, значит BP = 240, CP = 180, BC = 300

tg ∠ ВАС = , , , АС = 225

Из вершины прямого угла C треугольника ABC проведена высота CP . Радиус окружности, вписанной в треугольник BCP , равен 96, тангенс угла BAC равен . Найдите радиус окружности, вписанной в треугольник ABC .

Из вершины прямого угла C треугольника ABC проведена высота CP . Радиус окружности, вписанной в треугольник BCP , равен 24, тангенс угла BAC равен . Найдите радиус окружности, вписанной в треугольник ABC .

Из вершины прямого угла C треугольника ABC проведена высота CP . Радиус окружности, вписанной в треугольник ACP , равен 12 см, тангенс угла ABC равен 2,4 . Найдите радиус вписанной окружности треугольника ABC .

Биссектриса CM треугольника ABC делит сторону AB на отрезки AM =7 и MB =9 . Касательная к описанной окружности треугольника ABC , проходящая через точку C , пересекает прямую AB в точке D . Найдите CD .

∠ АВС – вписанный, ∠ АВС =

∠АСD – угол между диаметром и хордой, ∠ АСD = , следовательно ∠ АВС = ∠АСD

∆DBC ∾∆DCA ( по двум углам; ∠D – общий, ∠ DВС = ∠АСD)

= , (по свойству биссектрисы треугольника)

DB = DA + AB; = + 16 ⇨ DC = 36,5

Биссектриса CM треугольника ABC делит сторону AB на отрезки AM =5 и MB =10 . Касательная к описанной окружности треугольника ABC , проходящая через точку C , пересекает прямую AB в точке D . Найдите CD .

Биссектриса CM треугольника ABC делит сторону AB на отрезки AM =9 и MB =12 . Касательная к описанной окружности треугольника ABC , проходящая через точку C , пересекает прямую AB в точке D . Найдите CD .

Биссектриса CM треугольника ABC делит сторону AB на отрезки AM =10 и MB =18 . Касательная к описанной окружности треугольника ABC , проходящая через точку C , пересекает прямую AB в точке D . Найдите

В треугольнике ABC известны длины сторон AB =84 , AC =98 , точка O — центр окружности, описанной около треугольника ABC . Прямая BD , перпендикулярная прямой AO , пересекает сторону AC вточке D .
Найдите CD .

Пусть прямая BD, перпендикулярная прямой АО пересекает сторону АС в точке О, а окружность – в точке К. ВК ∩ АО = L.

Так как хорда ВК перпендикулярна диаметру АМ, то BL = KL и ᴗАВ = ᴗАК.

Следовательно ∠АСВ = ∠АВК (как вписанные углы, опирающиеся на равные дуги), значит

∆ABD ∾ ∆ACB (по двум углам: ∠А – общий, ∠АСВ = ∠АВК).

В треугольнике ABC известны длины сторон AB =40 , AC =64 , точка O — центр окружности, описанной около треугольника ABC . Прямая BD , перпендикулярная прямой AO , пересекает сторону AC вточке D .
Найдите CD .

В треугольнике ABC известны длины сторон AB =30 , AC =100 , точка O — центр окружности, описанной около треугольника ABC . Прямая BD , перпендикулярная прямой AO , пересекает сторону AC в точке D .
Найдите CD .

В треугольнике ABC известны длины сторон AB =12 , AC =72 , точка O — центр окружности, описанной около треугольника ABC . Прямая BD , перпендикулярная прямой AO , пересекает сторону AC в точке D .
Найдите CD .

В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 96. Найдите стороны треугольника ABC .

Пусть ВЕ – биссектриса АВС, АD – медиана АВС, ВЕ = АD = 96, ВЕ ⏊ АD.

∆ BOD = ∆ BOA (BO — общая, ∠ BOD = ∠ BOA = 90 ° , ∠ OBD = ∠ OBA), тогда АВ = BD = DC и AO = OD = 48

Пусть АВ = BD = DC = x

Проведем СF ⏊ BE. ∆ AOE ∾ ∆ CFE (по двум углам), значит , но (по свойству биссектрисы треугольника), тогда = ; , CF = 96

Так как BD = DC и OD ∥ FC, то по теореме Фалеса ВО = ОF.

Пусть OE = y, EF = 2y, тогда OB = 3y, BE = 4y; ВЕ = 96, 4у = 96, у = 24, ОВ = 72

В ∆ BOD: BOD = 90 ° , OD = 48, OB = 72, тогда BD = = = 8 = 24 ⇨ AB = BD = 24 , BC = 48

∆ AOE: AO = 48, OE = 24, AOE = 90 °; AE = = 24 ⇨ CE = 48 AC = 72 .

Ответ: 24 , 48 , 72 .

В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 168. Найдите стороны треугольника ABC .

В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 16. Найдите стороны треугольника ABC .

В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 164. Найдите стороны треугольника ABC .

Основание AC равнобедренного треугольника ABC равно 12. Окружность радиуса 7,5 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC .

В ∆ АВС АН = СН = 6( по условию)

СН = СЕ = СD = 6 (по свойству отрезков, касательных к окружности).

Проведем радиусы окружностей OD и KE; D и Е – точки касания окружностей с касательной ВС, следовательно OD ⏊ BC и KE ⏊ BC, значит OD ∥ KE, тогда четырёхугольник KEDO – трапеция.

Пусть КН = КЕ = х. Проведем КР ∥ ЕD. В ∆ОКР имеем: КР = 12, ОК = 7,5 + х, ОР = 7,5 – х

По теореме Пифагора: ОК 2 = ОР 2 + КР 2 ; (7,5 + х) 2 = (7,5 – х) 2 + 12 2

30х = 144; х = 4,8. Итак, R = х =4,8.

Основание AC равнобедренного треугольника ABC равно 12. Окружность радиуса 9 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC .

Основание AC равнобедренного треугольника ABC равно 8. Окружность радиуса 5 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC .

Основание AC равнобедренного треугольника ABC равно 10. Окружность радиуса 6 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC .

Окружности радиусов 25 и 100 касаются внешним образом. Точки A и B лежат на первой окружности, точки C и D — на второй. При этом AC и BD — общие касательные окружностей. Найдите расстояние между прямыми AB и CD .

Проведем радиусы окружностей ОА и РС. Так как радиусы проведены в точки касания окружностей с прямой АС, то они перпендикулярны к касательной: ОА ⏊ АС и РС ⏊ АС , следовательно ОА ∥ РС. Четырёхугольник ОАРС – трапеция. ОА = 25, РС = 100, ОР = 125. Проведем ОЕ ∥ АС. В ∆РОЕ: ∠ОЕР = 90°, РЕ = 100 – 25 = 75, ОР = 125. По теореме Пифагора

ОЕ 2 = ОР 2 – РЕ 2 , ОЕ = = = 100, ОЕ = АС = 100.

∆SOA ∾∆SPC (∠S – общий, ∠SAO =∠ SCP). , , 4 = 1 + , SA = .

∆SFC: cos , SC = SA + AC = , SF =

Окружности радиусов 45 и 55 касаются внешним образом. Точки A и B лежат на первой окружности, точки C и D — на второй. При этом AC и BD — общие касательные окружностей. Найдите расстояние между прямыми AB и CD .

Окружности радиусов 42 и 84 касаются внешним образом. Точки A и B лежат на первой окружности, точки C и D — на второй. При этом AC и BD — общие касательные окружностей. Найдите расстояние между прямыми AB и CD .

Окружности радиусов 4 и 60 касаются внешним образом. Точки A и B лежат на первой окружности, точки C и D — на второй. При этом AC и BD — общие касательные окружностей. Найдите расстояние между прямыми AB и CD .

Видео:3 правила для вписанного четырехугольника #shortsСкачать

По теме: методические разработки, презентации и конспекты

Логические задачи для 5 класса по математике

Логические задачи по математике для 5 класса, для детей, которые интересуются математикой.

Презентация «Ожившие задачи и теоремы» (ЖМ) учителя математики Монаковой Клары Захаровны.

Задачи на построение и теоремы (7-8 класс) выполнены в прогамме «Живая геометрия» как пример применения этой программы в преподавании геометрии.

Решение задач С4 на ЕГЭ по математике

Материал для консультации. Может быть полезен учителям и учащимся 9 — 11 классов при подготовке к экзаменам.

Задачи на работу. ЕГЭ по математике В13.

Решение задач на работу. Подробно, с объяснениями, разные типы задач (более десяти). Необходимо для подготовки к ЕГЭ по математике в части В13.

Задачи на работу. ЕГЭ по математике В13.

Решение задач на работу. С объяснениями, понятно доступно. Для выпускников, подготовка к ЕГЭ.

Задачи межпредметного смысла на уроках математики. Задачи природно — экологического содержания для 6 класса

Данная презентация содержит задачи экологической направленности и может быть полезна учителям математики при подготовке уроков и внеклассных мероприятий по ФГОС.

Методическая разработка по математике «Решение тестовых задач Единого Государственного Экзамена по математике: задачи на движение»

Решения тестовых задач ЕГЭ по математике по теме «Задачи на движение» всегда вызывают сложности у учащихся. Методическая разработка сделана для того ,чтоб было более ясно и проще выполнять данные зада.

Видео:Все типы четырёхугольников в задании №12 ЕГЭ по базовой математике + профильСкачать

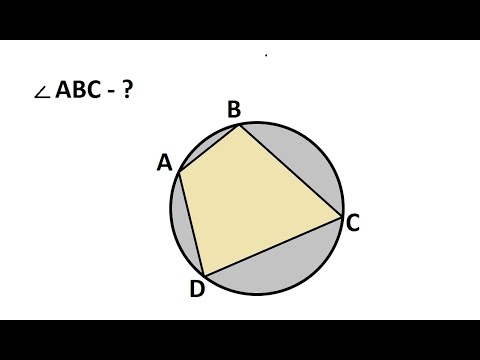
Четырехугольник ABCD вписан в окружность

Четырехугольник ABCD со сторонами AB=40 и CD=10 вписан в окружность. Диагонали AC и BD пересекаются в точке K, причём ∠AKB=60º. Найти радиус окружности, описанной около этого четырёхугольника.

Дано : ABCD — четырёхугольник, вписанный в окружность (O;R), AB=40, CD=10, AC∩BD=K, ∠AKB=60º

Радиус описанной около четырёхугольника окружности можно найти как радиус окружности, описанной около любого из треугольников, образованной вершинами четырёхугольника, например, около треугольника ABC. Если использовать формулу