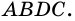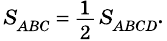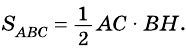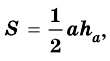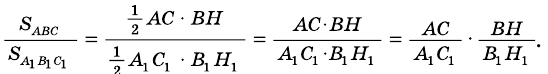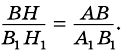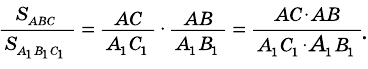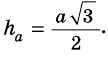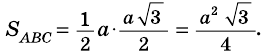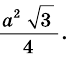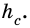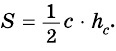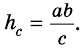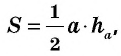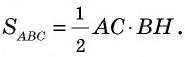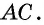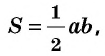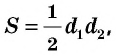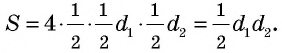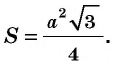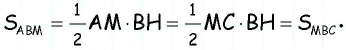Площадь треугольника с доказательством

Видео:9 класс, 12 урок, Теорема о площади треугольникаСкачать

Площадь треугольника — определение и вычисление с примерами решения

Площадь треугольника:

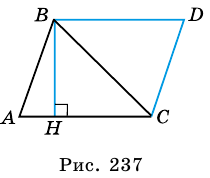
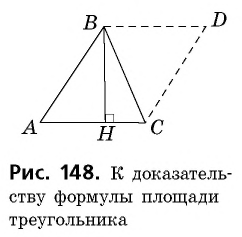
Теорема (о площади треугольника). Площадь треугольника равна половине произведения его стороны на высоту, к ней проведенную.

Доказательство:

Пусть

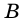
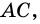
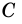
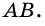
1) Проведем через вершину прямую, параллельную а через вершину — прямую, параллельную Получим параллелограмм

2) (по трем сторонам). Поэтому

откуда

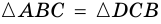
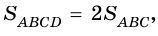
3) Так как 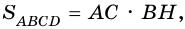то

В общем виде формулу площади 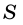треугольника можно записать так:

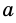
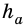
где — сторона треугольника, — высота, проведенная к ней.

Следствие 1. Площадь прямоугольного треугольника равна половине произведения катетов.

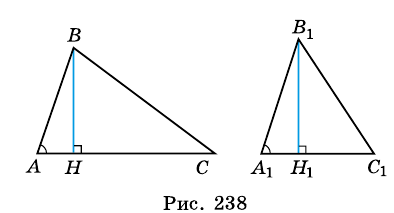
Следствие 2. Если сторона одного треугольника равна стороне другого треугольника, то площади таких треугольников относятся как их высоты, проведенные к этим сторонам.

Следствие 3. Если высота одного треугольника равна высоте другого треугольника, то площади этих треугольников относятся как стороны, к которым проведены эти высоты.

Пример:

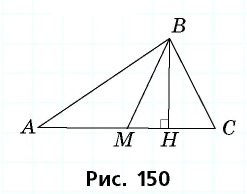
Докажите, что если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, образующих этот угол.

Доказательство:

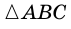
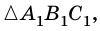
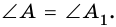
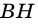
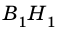
Рассмотрим и у которых Проведем высоты и (рис. 238).

2) (по острому углу), поэтому

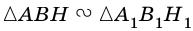
3) Имеем:

Пример:

Найдите площадь равностороннего треугольника, сторона которого равна

Решение:

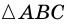
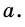
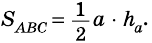
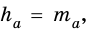
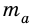
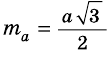
Пусть — равносторонний со стороной Тогда В равностороннем треугольнике где — медиана. Но (§ 18, задача 4), поэтому

Следовательно,

Ответ.

Пример:

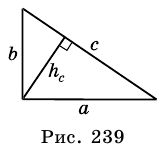
Стороны треугольника равны 8 см, 15 см и ^ 17 см. Найдите высоту треугольника, проведенную к его наибольшей стороне.

Решение:

Так как 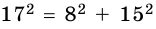(т. е. 289 = 289), то по теореме, обратной теореме Пифагора, треугольник является прямоугольным. Прямой угол является противолежащим к стороне, равной 17 см.

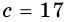
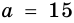
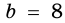
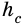
Пусть на рис. 239 изображен прямоугольный треугольник, у которого см -гипотенуза, и см — катеты, — высота. Найдем

Площадь этого треугольника можно найти

по формулам: 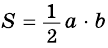или

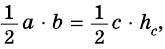
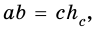
Тогда то есть откуда

Таким образом, имеем: 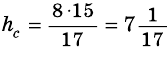(см).

Ответ. 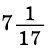см.

Видео:8 класс, 14 урок, Площадь треугольникаСкачать

Теорема (формула площади треугольника)

Площадь треугольника равна половине произведения его стороны на высоту, проведенную к этой стороне:

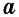
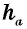
где — сторона треугольника, — проведенная к ней высота.

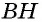
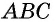
Пусть — высота треугольника (рис. 148). Докажем, что

Проведем через вершины прямые, параллельные сторонам треугольника, и обозначим точку их пересечения Таким образом, мы «достроили» треугольник до параллелограмма в котором отрезок также является высотой, проведенной к стороне

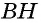
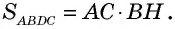
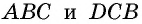
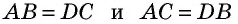
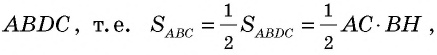
По формуле площади параллелограмма Треугольники равны по трем сторонам (у них сторона общая, как противолежащие стороны параллелограмма). Эти треугольники имеют равные площади. Тогда площадь треугольника составляет половину площади параллелограмма что и требовалось доказать.

Следствие 1

Площадь прямоугольного треугольника равна половине произведения его катетов:

где 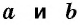— катеты прямоугольного треугольника.

Действительно, в прямоугольном треугольнике высота, проведенная к катету, совпадает с другим катетом.

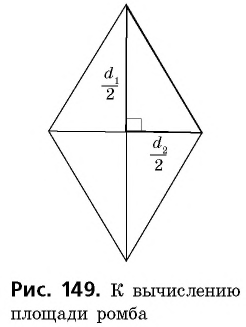
Следствие 2

Площадь ромба равна половине произведения его диагоналей:

где 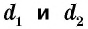— диагонали ромба.

Действительно, диагонали делят ромб на четыре равных прямоугольных треугольника с катетами 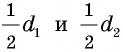(рис. 149). Используя следствие 1, имеем:

Следствие 3

Площадь равностороннего треугольника со стороной 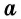вычисляется по формуле

Обоснуйте это следствие самостоятельно.

Опорная задача

Медиана делит треугольник на два равновеликих треугольника. Докажите.

Решение:

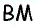
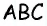
Пусть — медиана треугольника (рис. 150).

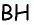
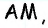
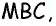
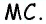
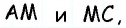
Проведем высоту треугольника Этот отрезок является одновременно высотой треугольника проведенной к стороне и высотой треугольника проведенной к стороне Учитывая равенство отрезков имеем:

Эта задача имеет интересные обобщения: если высоты двух треугольников равны, то отношение площадей этих треугольников равно отношению их оснований; если основания двух треугольников равны, то отношение площадей этих треугольников равно отношению их высот.

Докажите эти утверждения самостоятельно.

• Соотношения между сторонами и углами произвольного треугольника
• Окружность и круг
• Описанные и вписанные окружности
• Плоские и пространственные фигуры
• Взаимное расположения прямых на плоскости
• Треугольник
• Решение треугольников
• Треугольники и окружность

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Видео:Площадь треугольника. Как найти площадь треугольника?Скачать

Площадь треугольника

Видео:Геометрия 8 Площадь треугольникаСкачать

Определение площади треугольника

Площадь треугольника — это величина, которая
показывает какие размеры у треугольника.

Сейчас, на примере покажем, что такое площадь,
а также, как можно найти площадь треугольника.

Площадь треугольника, можно очень легко объяснить
на примере прямоугольного треугольника в клеточном поле.
Площадь, в нашем случае, будет равна количеству клеток.

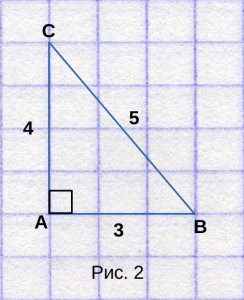
Для наглядности, нарисуем прямоугольный треугольник
ABC, со длинами сторон 3, 4 и 5, как на рисунке 2. Отметим, что он прямоугольный.

Посчитаем количество клеток, которые занимает треугольник.
3 полных клетки, и 4 неполных клетки, но для того, чтобы узнать
площадь треугольника в клеточном поле нам нужно узнать количество
полных клеток, которые занимает весь треугольник. Наша задача в том,
чтобы неполные клетки преобразовать в полные.

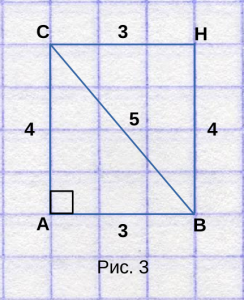
Для этого нарисуем второй треугольник, так,
чтобы получился прямоугольник, как на рисунке 3.

Как видим, весь прямоугольник занимает 12 полных клеток.

Формула площади прямоугольника равна произведению
одной стороны на другую — ​ ( S = ab ) ​,
поэтому площадь прямоугольника равна 3 * 4 = 12 клеткам.

Площадь треугольника, из которого состоит прямоугольник,
можно найти по другой формуле: ​ ( S = frac2 ab ) ​.
Подставив значения длин сторон, получаем — S = 0.5 * 3 * 4,
из чего следует, что S = 6 клетками, или же квадратным сантиметрам.

Прямоугольник можно условно разделить
на два треугольника, поэтому площадь треугольника
равна половине площади прямоугольника.

Формула площади треугольника — это формула,
по которой можно найти площадь треугольника.

Формулы площади треугольника применяют, только,
и только тогда, когда невозможно узнать площадь
треугольника, глядя на рисунок, или просто посчитав клетки.

Видео:Геометрия 9 класс (Урок№14 - Теорема о площади треугольника.)Скачать

Формулы площади треугольника

Ⅰ. Через высоту и основание

a — сторона, на которую падает высота,
b — высота.

Самая известная формула площади треугольника.
Зная только высоту и сторону, на которую падает
эта высота, можно найти площадь треугольника.

Ⅱ. Через все стороны и периметр

p — полупериметр, вычисляется по формуле: ​ ( p = frac ) ​,
a, b, c — стороны треугольника.

Это формулу, нужно использовать когда известны
все три стороны треугольника. Зная три стороны
треугольника можно найти периметр, а дальше
найти и площадь заданного треугольника.

Эту формулу площади также называют формулой Герона.

Ⅲ. Через две стороны и угол между ними

[ S = frac a cdot b cdot sin β ]

a, b — стороны между которыми расположен угол β,
sin β — синус угла β.

Формула применяется, когда известен
один из углов, и две стороны, образующие
этот угол. В некоторых задачах площадь
треугольника можно найти только по этой формуле.

Ⅳ. Через периметр и радиус вписанной окружности

[ S = r cdot frac

2 ]

r — радиус вписанной окружности,
P — периметр треугольника.

Тут даже не обязательно знать все стороны треугольника,
достаточно знать периметр и радиус описанной окружности.

Ⅴ. Через все стороны и радиус описанной окружности

abc — произведение всех сторон треугольника,
R — радиус описанной окружности.

Пожалуй, единственная формула, где площадь
треугольника можно найти только через радиус
описанной окружности и произведение трех сторон.

Ⅵ. Через сторону и два прилежащих к ней угла

a — сторона треугольника,
sin α — синус угла α,
sin β — синус угла β.

Готов поспорить, вы даже ни разу не видели этой формулы.
Эта очередная формула площади треугольника, применяется
в крайне редких случаях — когда известны два угла и сторона,
к которой эти углы примыкают.

Видео:✓ Новая формула площади треугольника | Ботай со мной #108 | Борис ТрушинСкачать

Как найти площадь треугольника – все способы от самых простых до самых сложных

Зависит от того, какой треугольник.

Чтобы найти площадь треугольника, надо сначала определить тип треугольника: прямоугольный, равнобедренный, равносторонний. Если он у вас не такой – отталкивайтесь от других данных: высоты, вписанной или описанной окружности, длин сторон. Привожу все формулы ниже.

Видео:Площадь треугольника. Формула площади. Геометрия 8 класс.Скачать

Если треугольник прямоугольный

То есть один из его углов равен 90 градусам.

Надо перемножить катеты и поделить на два. Катеты – это две меньшие стороны, в сравнении с гипотенузой. Гипотенуза – это самая длинная сторона, она всегда находится напротив угла в 90 градусов.

Видео:Геометрия 8 класс (Урок№10 - Площадь треугольника.)Скачать

Если он равнобедренный

То есть у него равны боковые стороны. В таком случае надо провести высоту к основанию (той стороне, которая не равна «бедрам»), перемножить высоту с основанием и поделить результат на два.

Видео:Геометрия Доказательство Площадь треугольника равна половине произведения двух его сторон и синусаСкачать

Если он равносторонний

То есть все три стороны равны. Ваши действия такие:

1. Найдите квадрат стороны – умножьте эту сторону на нее же. Если у вас сторона равна 4, умножьте 4 на 4, будет 16.
2. Умножьте полученное значение на корень из 3. Это примерно 1,732050807568877293527.
3. Поделите все на 4.

Видео:100. Теорема о площади треугольникаСкачать

Если известна сторона и высота

Площадь любого треугольника равна половине произведения стороны на высоту, которая к этой стороне проведена. Именно к этой, а не к какой-то другой.

Чтобы провести высоту к стороне, надо найти вершину (угол), которая противоположна этой стороне, а потом опустить из нее на сторону прямую линию под углом в 90 градусов. На картинке высота обозначена синим цветом и буквой h, а линия, на которую она опускается, красным цветом и буквой a.

Видео:Площади треугольников с равным углом.Скачать

Если известны две стороны и градус угла между ними

Если вы знаете, чему равны две стороны и угол между ними, то надо найти синус этого угла, умножить его на первую сторону, умножить на вторую и еще умножить на ½:

Видео:Геометрия Доказательство Площадь треугольника равна произведению его полупериметра и радиусаСкачать

Если известны длины трех сторон

1. Найдите периметр. Для этого сложите все три стороны.
2. Найдите полупериметр – разделите периметр на два. Запомните значение.
3. Отнимите от полупериметра длину первой стороны. Запомните.
4. Отнимите от полупериметра длину второй стороны. Тоже запомните.
5. Отнимите от полупериметра длину третьей стороны. И ее запомните.
6. Умножьте полупериметр на каждое из этих чисел (разницу с первой, второй и третьей стороной).
7. Найдите квадратный корень.

Эта формула еще называется формулой Герона. Возьмите на заметку, если вдруг учитель спросит.

Видео:Площадь по теореме Герона #математика #площадь #треугольник #герона #егэ #огэ #найтиплощадь #теоремаСкачать

Если известны три стороны и радиус описанной окружности

Окружность вы можете описать вокруг любого треугольника. Чтобы найти площадь «вписанного» треугольника – того, который «вписался» в окружность, надо перемножить три его стороны и поделить их на четыре радиуса. Смотрите картинку.

Видео:Отношение площадей треугольников с равным угломСкачать

Если известны три стороны и радиус вписанной окружности

Если вам удалось вписать в треугольник окружность, значит она обязательно касается каждой из его сторон. Следовательно, расстояние от центра окружности до каждой из сторон треугольника – ее радиус.

Чтобы найти площадь, посчитайте сначала полупериметр – сложите все стороны и поделите на два. А потом умножьте его на радиус.

Это были все способы найти площадь треугольника. Спасибо, что дочитали статью до конца. Лайкните, если не трудно.

🎬 Видео

Почему площадь треугольника равна половине произведения основания на высотуСкачать

Отношение площадей треугольниковСкачать

8 класс, 21 урок, Отношение площадей подобных треугольниковСкачать

Секретные формулы площади треугольникаСкачать

Теорема о площади треугольника.Скачать

Теорема о площади треугольника по двум сторонам и углу между ними. Доказательство. Геометрия 9 классСкачать