Длина вектора в ортонормированном базисе теорема

Дата добавления: 2015-09-15 ; просмотров: 7035 ; Нарушение авторских прав

Для определения положения произвольной точки могут использоваться различные системы координат. Положение произвольной точки в какой- либо системе координат должно однозначно определяться. Понятие системы координат представляет собой совокупность точки начала отсчета (начала координат) и некоторого базиса. Как на плоскости, так и в пространстве возможно задание самых разнообразных систем координат. Выбор системы координат зависит от характера поставленной геометрической, физической или технической задачи. Рассмотрим некоторые наиболее часто применяемые на практике системы координат.

Декартова система координат.

Зафиксируем в пространстве точку О и рассмотрим произвольную точку М.

Вектор назовем радиус- вектором точки М. Если в пространстве задать некоторый базис, то точке М можно сопоставить некоторую тройку чисел – компоненты ее радиус- вектора.

Определение. Декартовой системой координат в пространстве называется совокупность точки и базиса. Точка называется началом координат. Прямые, проходящие через начало координат называются осями координат.

1-я ось – ось абсцисс

2-я ось – ось ординат

3-я ось – ось апликат

Чтобы найти компоненты вектора нужно из координат его конца вычесть координаты начала.

Если заданы точки А(x₁, y₁, z₁), B(x₂, y₂, z₂), то = (x₂ – x₁, y₂ – y₁, z₂ – z₁).

Определение. Базис называется ортонормированным, если его векторы попарно ортогональны и равны единице.

Определение. Декартова система координат, базис которой ортонормирован называется декартовой прямоугольной системой координат.

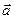
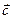
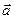
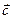
Пример. Даны векторы (1; 2; 3), (-1; 0; 3), (2; 1; -1) и (3; 2; 2) в некотором базисе. Показать, что векторы , и образуют базис и найти координаты вектора в этом базисе.

Векторы образуют базис, если они линейно независимы, другими словами, если уравнения, входящие в систему:

линейно независимы.

Тогда .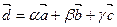

Это условие выполняется, если определитель матрицы системы отличен от нуля.

Для решения этой системы воспользуемся методом Крамера.

D₁ =

;

D₂ =

D₃ =

Итого, координаты вектора в базисе , , : .

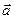
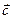
Длина вектора в координатах определяется как расстояние между точками начала и конца вектора. Если заданы две точки в пространстве А(х₁, y₁, z₁), B(x₂, y₂, z₂), то .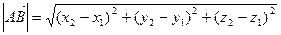

1. Деление вектора в заданном отношении. Операции над векторами, заданными своими координатами.

Если точка М(х, у, z) делит отрезок АВ в соотношении l/m, то координаты этой точки определяются как:

В частном случае координаты середины отрезка находятся как:

Линейные операции над векторами в координатах.

Видео:Нахождение длины вектора через координаты. Практическая часть. 9 класс.Скачать

35. Ортонормированные базисы в евклидовом пространстве

Определение 51. Базис Е = (Е1, Е2, . , Еn) пространства Еn называется Ортонормированным, если все его векторы единичные и попарно ортогональные.

Замечание. В примере 1 пункта 7.2 заданный базис является ортонормированным. Во втором примере этого пункта базис не ортонормированный.

Если базисные векторы единичные, но не все попарно ортогональны, то базис называется Нормированным. Если базисные векторы попарно ортогональны, но не все единичные, то базис называется Ортогональным.

Теорема 43. Любой базис евклидова пространства можно ортонормировать.

Доказательство. Пусть Е = (Е1, Е2, . , Еn) – произвольный базис пространства Еn. Доказательство проведём в два этапа. Сначала на основе данного базиса получим ортогональный базис, а затем полученный базис нормируем.

Пусть Е11 = Е1. Если Е2 ^ Е1, То возьмём Е21 = Е2. Если Е2 не ортогонален Е1. то найдём коэффициент A Так, чтобы вектор Е21 = AЕ1 + Е2 Был ортогонален вектору Е11. Так как вектор Е21 ¹ 0, то для этого необходимо и достаточно, чтобы (Е11, е21 ) = 0, т. е. (Е1, AЕ1 + Е2) = 0. Отсюда AЕ12 + (Е1, Е2) = 0. Так как Е1 ¹ 0. то Так как Е11 и Е21 ортогональны, то они линейно независимы. Вектор Е31 Будем искать в виде Е31 = A1 Е11 + A2 Е21 + Е3. Для того, чтобы Е31 был ортогонален Е11 И Е21, необходимо и достаточно, чтобы (Е11, Е31) = (Е21, Е31) = 0. Получаем систему

Так как определитель этой системы отличен от нуля (по формуле 43) то система имеет и только одно решение. Следовательно,

Вектор Е31 найдётся и только один. Так как векторы Е11, е21, е31 попарно ортогональны, то они линейно независимы. Если векторы Е11, е21, … , еn–11 уже получены, то вектор Еn1 будем искать в виде Еn1 = B1×Е11+ B2× е21 + … + Bn–1× еn–11 + Еn . Так как вектор Еn1 должен быть ортогонален ко всем предыдущим, то для нахождения коэффициентов B1, B2, … , Bn–1 получим систему уравнений (Е11, Еn1) = (Е21, Еn1) = … = (Еn–11, Еn1) = 0. Можно показать, что эта система всегда имеет решение и только одно. Итак, базис Е1 = (Е11, Е21, . , Еn1) –ортогональный. Разделив каждый полученный вектор на его длину, получим ортонормированный базис.

Теорема 44. Скалярное произведение в ортонормированном базисе имеет единичную матрицу Грама.

Доказательство Следует из того, что в ортонормированном базисе (Ек, ек) =1, (Ек, еs )= 0, если К ¹ s.

Следствие. Если вектор А В ортонормированном базисе имеет координаты (Х1, х2,…, хn), то ½А½= (47).

Теорема 45. Определитель матрицы Грама и все её главные угловые миноры строго положительны.

Доказательство. Пусть в данном (но произвольном) базисе матрица Грама имеет вид

Г = .

Пусть Е = (Е1, Е2, . , Еn) ортонормированный базис и Т – матрица перехода от данного базиса к базису Е. В базисе Е Матрица Грама – единичная. По формуле (43) Е = ТТ×Г×Т. Отсюда 1 = |Г |×|Т |2. Так как |Т |2 > 0,

Так как – евклидово подпространство пространства Еn с Тем же скалярным произведением, то главный угловой минор матрицы Г будет для него матрицей Грама. Но тогда, по доказанному, этот минор положителен.

Примеры. Могут ли быть матрицами Грама следующие матрицы.

1. А =

Матрица А Не может быть матрицей Грама, так как в матрице Грама все диагональные элементы должны быть положительными.

2. В =

Матрица В Не может быть матрицей Грама, так как матрица Грама должна быть симметрична относительно главной диагонали.

3. С =

Матрица С Не может быть матрицей Грама, так как |С | = –81 0, = 7 > 0. Следовательно, D является матрицей Грама.

Доказательство. В ортонормированном базисе скалярное произведение имеет единичную матрицу, поэтому

(А, В) = ХТ×Е×у = ХТ×у = (Х1, х2, … , хn) × = Х1у1 + Х2у2 + … + Хnуn.

Пример. В пространстве Е4 задан ортонормированный базис и векторы А1= (2, 1, 1, 2) и А2 = (–3, 2, –5, 1). Найти ортогональное дополнение к линейной оболочке L = .

Решение. Если L^, то В Î L^ Û (А1, В) = (А2, В) = 0. Пусть В = (Х1, х2, х3, х4). Так как базис ортонормированный, то (А1, В) = 2Х1 + х2 + х3 + 2Х4 , (А2, В) = –3Х1 + 2Х2 –5Х3 + х4 . Следовательно, В Î L^ Û Решая эту систему, получим, что

В = (–С1 –3С2 , С1 – 8С2 , С1 , 7С2), где С1 , С2 – любые действительные числа.

Отсюда следует, что L^ — двумерное линейное пространство, натянутое на векторы

Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Векторное пространство: размерность и базис, разложение вектора по базису

В статье о n -мерных векторах мы пришли к понятию линейного пространства, порождаемого множеством n -мерных векторов. Теперь нам предстоит рассмотреть не менее важные понятия, такие как размерность и базис векторного пространства. Они напрямую связаны с понятием линейно независимой системы векторов, так что дополнительно рекомендуется напомнить себе основы и этой темы.

Введем некоторые определения.

Размерность векторного пространства – число, соответствующее максимальному количеству линейно независимых векторов в этом пространстве.

Базис векторного пространства – совокупность линейно независимых векторов, упорядоченная и в своей численности равная размерности пространства.

Рассмотрим некое пространство n -векторов. Размерность его соответственно равна n . Возьмем систему из n -единичных векторов:

e ( 1 ) = ( 1 , 0 , . . . , 0 ) e ( 2 ) = ( 0 , 1 , . . . , 0 ) e ( n ) = ( 0 , 0 , . . . , 1 )

Используем эти векторы в качестве составляющих матрицы A : она будет являться единичной с размерностью n на n . Ранг этой матрицы равен n . Следовательно, векторная система e ( 1 ) , e ( 2 ) , . . . , e ( n ) является линейно независимой. При этом к системе невозможно добавить ни одного вектора, не нарушив ее линейной независимости.

Так как число векторов в системе равно n , то размерность пространства n -мерных векторов равна n , а единичные векторы e ( 1 ) , e ( 2 ) , . . . , e ( n ) являются базисом указанного пространства.

Из полученного определения сделаем вывод: любая система n -мерных векторов, в которой число векторов меньше n , не является базисом пространства.

Если мы поменяем местами первый и второй вектор, получим систему векторов e ( 2 ) , e ( 1 ) , . . . , e ( n ) . Она также будет являться базисом n -мерного векторного пространства. Составим матрицу, взяв за ее строки векторы полученной системы. Матрица может быть получена из единичной матрицы перестановкой местами первых двух строк, ранг ее будет равен n . Система e ( 2 ) , e ( 1 ) , . . . , e ( n ) линейно независима и является базисом n -мерного векторного пространства.

Переставив местами в исходной системе другие векторы, получим еще один базис.

Мы можем взять линейно независимую систему неединичных векторов, и она также будет представлять собой базис n -мерного векторного пространства.

Векторное пространство с размерностью n имеет столько базисов, сколько существует линейно независимых систем из n -мерных векторов числом n.

Плоскость является двумерным пространством – ее базисом будут два любых неколлинеарных вектора. Базисом трехмерного пространства послужат три любых некомпланарных вектора.

Рассмотрим применение данной теории на конкретных примерах.

Исходные данные: векторы

a = ( 3 , — 2 , 1 ) b = ( 2 , 1 , 2 ) c = ( 3 , — 1 , — 2 )

Необходимо определить, являются ли указанные векторы базисом трехмерного векторного пространства.

Решение

Для решения поставленной задачи исследуем заданную систему векторов на линейную зависимость. Составим матрицу, где строки – координаты векторов. Определим ранг матрицы.

A = 3 2 3 — 2 1 — 1 1 2 — 2 A = 3 — 2 1 2 1 2 3 — 1 — 2 = 3 · 1 · ( — 2 ) + ( — 2 ) · 2 · 3 + 1 · 2 · ( — 1 ) — 1 · 1 · 3 — ( — 2 ) · 2 · ( — 2 ) — 3 · 2 · ( — 1 ) = = — 25 ≠ 0 ⇒ R a n k ( A ) = 3

Следовательно, заданные условием задачи векторы линейно независимы, и их численность равна размерности векторного пространства – они являются базисом векторного пространства.

Ответ: указанные векторы являются базисом векторного пространства.

Исходные данные: векторы

a = ( 3 , — 2 , 1 ) b = ( 2 , 1 , 2 ) c = ( 3 , — 1 , — 2 ) d = ( 0 , 1 , 2 )

Необходимо определить, может ли указанная система векторов являться базисом трехмерного пространства.

Решение

Указанная в условии задачи система векторов является линейно зависимой, т.к. максимальное число линейно независимых векторов равно 3. Таким образом, указанная система векторов не может служить базисом трехмерного векторного пространства. Но стоит отметить, что подсистема исходной системы a = ( 3 , — 2 , 1 ) , b = ( 2 , 1 , 2 ) , c = ( 3 , — 1 , — 2 ) является базисом.

Ответ: указанная система векторов не является базисом.

Исходные данные: векторы

a = ( 1 , 2 , 3 , 3 ) b = ( 2 , 5 , 6 , 8 ) c = ( 1 , 3 , 2 , 4 ) d = ( 2 , 5 , 4 , 7 )

Могут ли они являться базисом четырехмерного пространства?

Решение

Cоставим матрицу, используя в качестве строк координаты заданных векторов

A = 1 2 3 3 2 5 6 8 1 3 2 4 2 5 4 7

По методу Гаусса определим ранг матрицы:

A = 1 2 3 3 2 5 6 8 1 3 2 4 2 5 4 7

1 2 3 3 0 1 0 2 0 1 — 1 1 0 1 — 2 1

1 2 3 3 0 1 0 2 0 0 — 1 — 1 0 0 — 2 — 1

1 2 3 3 0 1 0 2 0 0 — 1 — 1 0 0 0 1 ⇒ ⇒ R a n k ( A ) = 4

Следовательно, система заданных векторов линейно независима и их численность равна размерности векторного пространства – они являются базисом четырехмерного векторного пространства.

Ответ: заданные векторы являются базисом четырехмерного пространства.

Исходные данные: векторы

a ( 1 ) = ( 1 , 2 , — 1 , — 2 ) a ( 2 ) = ( 0 , 2 , 1 , — 3 ) a ( 3 ) = ( 1 , 0 , 0 , 5 )

Составляют ли они базис пространства размерностью 4?

Решение

Исходная система векторов линейно независима, но численность векторов в ней недостаточна, чтобы стать базисом четырехмерного пространства.

Ответ: нет, не составляют.

Видео:Длина вектора через координаты. 9 класс.Скачать

Разложение вектора по базису

Примем, что произвольные векторы e ( 1 ) , e ( 2 ) , . . . , e ( n ) являются базисом векторного n-мерного пространства. Добавим к ним некий n -мерный вектор x → : полученная система векторов станет линейно зависимой. Свойства линейной зависимости гласят, что хотя бы один из векторов такой системы может линейно выражаться через остальные. Переформулируя это утверждение, можно говорить о том, что хотя бы один из векторов линейно зависимой системы может раскладываться по остальным векторам.

Таким образом, мы пришли к формулировке важнейшей теоремы:

Любой вектор n -мерного векторного пространства единственным образом раскладывается по базису.

Докажем эту теорему:

зададим базис n -мерного векторного пространства — e ( 1 ) , e ( 2 ) , . . . , e ( n ) . Сделаем систему линейно зависимой, добавив к ней n -мерный вектор x → . Этот вектор может быть линейно выражен через исходные векторы e :

x = x 1 · e ( 1 ) + x 2 · e ( 2 ) + . . . + x n · e ( n ) , где x 1 , x 2 , . . . , x n — некоторые числа.

Теперь докажем, что такое разложение является единственным. Предположим, что это не так и существует еще одно подобное разложение:

Отнимем от левой и правой частей этого равенства соответственно левую и правую части равенства x = x 1 · e ( 1 ) + x 2 · e ( 2 ) + . . . + x n · e ( n ) . Получим:

1 — x 1 ) · e ( 1 ) + ( x

2 — x 2 ) · e ( 2 ) + . . . ( x

Система базисных векторов e ( 1 ) , e ( 2 ) , . . . , e ( n ) линейно независима; по определению линейной независимости системы векторов равенство выше возможно только тогда, когда все коэффициенты ( x

2 — x 2 ) , . . . , ( x

n — x n ) будут равны нулю. Из чего справедливым будет: x 1 = x

n . И это доказывает единственный вариант разложения вектора по базису.

При этом коэффициенты x 1 , x 2 , . . . , x n называются координатами вектора x → в базисе e ( 1 ) , e ( 2 ) , . . . , e ( n ) .

Доказанная теория делает понятным выражение «задан n -мерный вектор x = ( x 1 , x 2 , . . . , x n ) »: рассматривается вектор x → n -мерного векторного пространства, и его координаты заданы в некотором базисе. При этом также понятно, что этот же вектор в другом базисе n -мерного пространства будет иметь другие координаты.

Рассмотрим следующий пример: допустим, что в некотором базисе n -мерного векторного пространства задана система из n линейно независимых векторов

e ( 1 ) = ( e 1 ( 1 ) , e 2 ( 1 ) , . . . , e n ( 1 ) ) e ( 2 ) = ( e 1 ( 2 ) , e 2 ( 2 ) , . . . , e n ( 2 ) ) ⋮ e ( n ) = ( e 1 ( n ) , e 2 ( n ) , . . . , e n ( n ) )

а также задан вектор x = ( x 1 , x 2 , . . . , x n ) .

Векторы e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) в этом случае также являются базисом этого векторного пространства.

Предположим, что необходимо определить координаты вектора x → в базисе e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) , обозначаемые как x

Вектор x → будет представлен следующим образом:

2 · e ( 2 ) + . . . + x

Запишем это выражение в координатной форме:

( x 1 , x 2 , . . . , x n ) = x

1 · ( e ( 1 ) 1 , e ( 1 ) 2 , . . . , e ( 1 ) n ) + x

2 · ( e ( 2 ) 1 , e ( 2 ) 2 , . . . , e ( 2 ) n ) + . . . + + x

n · ( e ( n ) 1 , e ( n ) 2 , . . . , e ( n ) n ) = = ( x

2 e 1 ( 2 ) + . . . + x

2 e 2 ( 2 ) + + . . . + x

n e 2 ( n ) , . . . , x

2 e n ( 2 ) + . . . + x

Полученное равенство равносильно системе из n линейных алгебраических выражений с n неизвестными линейными переменными x

n e 2 n ⋮ x n = x

Матрица этой системы будет иметь следующий вид:

e 1 ( 1 ) e 1 ( 2 ) ⋯ e 1 ( n ) e 2 ( 1 ) e 2 ( 2 ) ⋯ e 2 ( n ) ⋮ ⋮ ⋮ ⋮ e n ( 1 ) e n ( 2 ) ⋯ e n ( n )

Пусть это будет матрица A , и ее столбцы – векторы линейно независимой системы векторов e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) . Ранг матрицы – n , и ее определитель отличен от нуля. Это свидетельствует о том, что система уравнений имеет единственное решение, определяемое любым удобным способом: к примеру, методом Крамера или матричным методом. Таким образом мы сможем определить координаты x

n вектора x → в базисе e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) .

Применим рассмотренную теорию на конкретном примере.

Исходные данные: в базисе трехмерного пространства заданы векторы

e ( 1 ) = ( 1 , — 1 , 1 ) e ( 2 ) = ( 3 , 2 , — 5 ) e ( 3 ) = ( 2 , 1 , — 3 ) x = ( 6 , 2 , — 7 )

Необходимо подтвердить факт, что система векторов e ( 1 ) , e ( 2 ) , e ( 3 ) также служит базисом заданного пространства, а также определить координаты вектора х в заданном базисе.

Решение

Система векторов e ( 1 ) , e ( 2 ) , e ( 3 ) будет являться базисом трехмерного пространства, если она линейно независима. Выясним эту возможность, определив ранг матрицы A , строки которой – заданные векторы e ( 1 ) , e ( 2 ) , e ( 3 ) .

Используем метод Гаусса:

A = 1 — 1 1 3 2 — 5 2 1 — 3

1 — 1 1 0 5 — 8 0 3 — 5

1 — 1 1 0 5 — 8 0 0 — 1 5

R a n k ( A ) = 3 . Таким образом, система векторов e ( 1 ) , e ( 2 ) , e ( 3 ) линейно независима и является базисом.

Пусть в базисе вектор x → имеет координаты x

3 . Связь этих координат определяется уравнением:

3 e 1 ( 3 ) x 2 = x

3 e 2 ( 3 ) x 3 = x

Применим значения согласно условиям задачи:

Решим систему уравнений методом Крамера:

∆ = 1 3 2 — 1 2 1 1 — 5 — 3 = — 1 ∆ x

1 = 6 3 2 2 2 1 — 7 — 5 — 3 = — 1 , x

1 ∆ = — 1 — 1 = 1 ∆ x

2 = 1 6 2 — 1 2 1 1 — 7 — 3 = — 1 , x

2 ∆ = — 1 — 1 = 1 ∆ x

3 = 1 3 6 — 1 2 2 1 — 5 — 7 = — 1 , x

Так, вектор x → в базисе e ( 1 ) , e ( 2 ) , e ( 3 ) имеет координаты x

Ответ: x = ( 1 , 1 , 1 )

Видео:Доказать, что векторы a, b, c образуют базис и найти координаты вектора d в этом базисеСкачать

Связь между базисами

Предположим, что в некотором базисе n-мерного векторного пространства даны две линейно независимые системы векторов:

c ( 1 ) = ( c 1 ( 1 ) , c 2 ( 1 ) , . . . , c n ( 1 ) ) c ( 2 ) = ( c 1 ( 2 ) , c 2 ( 2 ) , . . . , c n ( 2 ) ) ⋮ c ( n ) = ( c 1 ( n ) , e 2 ( n ) , . . . , c n ( n ) )

e ( 1 ) = ( e 1 ( 1 ) , e 2 ( 1 ) , . . . , e n ( 1 ) ) e ( 2 ) = ( e 1 ( 2 ) , e 2 ( 2 ) , . . . , e n ( 2 ) ) ⋮ e ( n ) = ( e 1 ( n ) , e 2 ( n ) , . . . , e n ( n ) )

Указанные системы являются также базисами заданного пространства.

n ( 1 ) — координаты вектора c ( 1 ) в базисе e ( 1 ) , e ( 2 ) , . . . , e ( 3 ) , тогда связь координат будет задаваться системой линейных уравнений:

1 ( 1 ) e 1 ( 1 ) + c

2 ( 1 ) e 1 ( 2 ) + . . . + c

n ( 1 ) e 1 ( n ) с 2 ( 1 ) = c

1 ( 1 ) e 2 ( 1 ) + c

2 ( 1 ) e 2 ( 2 ) + . . . + c

n ( 1 ) e 2 ( n ) ⋮ с n ( 1 ) = c

1 ( 1 ) e n ( 1 ) + c

2 ( 1 ) e n ( 2 ) + . . . + c

В виде матрицы систему можно отобразить так:

( c 1 ( 1 ) , c 2 ( 1 ) , . . . , c n ( 1 ) ) = ( c

n ( 1 ) ) · e 1 ( 1 ) e 2 ( 1 ) … e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) … e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) … e n ( n )

Сделаем по аналогии такую же запись для вектора c ( 2 ) :

( c 1 ( 2 ) , c 2 ( 2 ) , . . . , c n ( 2 ) ) = ( c

n ( 2 ) ) · e 1 ( 1 ) e 2 ( 1 ) … e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) … e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) … e n ( n )

И, далее действуя по тому же принципу, получаем:

( c 1 ( n ) , c 2 ( n ) , . . . , c n ( n ) ) = ( c

n ( n ) ) · e 1 ( 1 ) e 2 ( 1 ) … e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) … e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) … e n ( n )

Матричные равенства объединим в одно выражение:

c 1 ( 1 ) c 2 ( 1 ) ⋯ c n ( 1 ) c 1 ( 2 ) c 2 ( 2 ) ⋯ c n ( 2 ) ⋮ ⋮ ⋮ ⋮ c 1 ( n ) c 2 ( n ) ⋯ c n ( n ) = c

n ( n ) · e 1 ( 1 ) e 2 ( 1 ) ⋯ e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) ⋯ e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) ⋯ e n ( n )

Оно и будет определять связь векторов двух различных базисов.

Используя тот же принцип, возможно выразить все векторы базиса e ( 1 ) , e ( 2 ) , . . . , e ( 3 ) через базис c ( 1 ) , c ( 2 ) , . . . , c ( n ) :

e 1 ( 1 ) e 2 ( 1 ) ⋯ e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) ⋯ e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) ⋯ e n ( n ) = e

n ( n ) · c 1 ( 1 ) c 2 ( 1 ) ⋯ c n ( 1 ) c 1 ( 2 ) c 2 ( 2 ) ⋯ c n ( 2 ) ⋮ ⋮ ⋮ ⋮ c 1 ( n ) c 2 ( n ) ⋯ c n ( n )

Дадим следующие определения:

n ( n ) является матрицей перехода от базиса e ( 1 ) , e ( 2 ) , . . . , e ( 3 )

к базису c ( 1 ) , c ( 2 ) , . . . , c ( n ) .

n ( n ) является матрицей перехода от базиса c ( 1 ) , c ( 2 ) , . . . , c ( n )

к базису e ( 1 ) , e ( 2 ) , . . . , e ( 3 ) .

📸 Видео

Разложение вектора по базису. 9 класс.Скачать

Как разложить вектор по базису - bezbotvyСкачать

Аналитическая геометрия, 1 урок, Векторы в пространствеСкачать

Векторное произведение: определение, свойства, вычисление в ортонормированном базисе.Скачать

Математика без Ху!ни. Смешанное произведение векторовСкачать

Лекция 16. Понятие вектора и векторного пространства. Базис векторного пространства.Скачать

§48 Ортонормированный базис евклидова пространстваСкачать

Координаты вектора. 9 класс.Скачать

18+ Математика без Ху!ни. Векторное произведение.Скачать

Нахождение длины вектора. Практическая часть. 9 класс.Скачать

Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Разложение вектора по векторам (базису). Аналитическая геометрия-1Скачать

A.7.4 Ортогонализация набора векторов. Процесс Грама-Шмидта.Скачать

МОДУЛЬ ВЕКТОРА длина вектора 10 и 11 классСкачать

Вывод формулы скалярного произведения векторов, заданных координатами в ортонормированном базисе.Скачать

Равенство векторов, Длина вектора.Как найти длину вектора?Скачать